反向传播理论推导

希望本文成为你见过的反向传播理论中最易理解的解释和最简洁形式的公式推导 😃

反向传播是上世纪80年代提出的训练神经网络的一种方法，在每次迭代训练时修改对每个神经元输入的权值，来达到最后一层的输出与期望的输出的总误差最小的目的。反向传播算法可以说是梯度下降在链式法则中的应用。

反向传播与梯度下降

Q：为什么会提出反向传播算法，直接应用梯度下降（Gradient Descent）不行吗？

梯度下降可以应对带有明确求导函数的情况（容易求解析解的情况），比如逻辑回归（Logistic Regression），我们可以把它看做没有隐层的网络；但对于多层神经网络，损失函数对前边的参数计算解析解导数，将十分复杂。而如果要数值解（函数的导数在某个点的数值），就很容易计算，直接根据导数的定义就能得到。

$$\frac{\partial C}{\partial w_j}\approx \frac{C(w+ϵe_j)-C(w)}{ϵ}$$

式中 cost function 看作权重的函数 $C=C(w)$, 忽略了偏置bias（其导数计算与w类似）。其中$ϵ$是一个大于零的很小的正数，$e_j$ 表示单位向量（方向坐标）。

通过这个导数的定义来计算梯度，实现比较简单，能够直接应用梯度下降来更新模型参数。然而网络参数量通常都很大，这种求解方式的计算量也会非常大，原因如下：

对于每一个权重$w_j$，计算梯度$\frac{\partial C}{\partial w_j}$时需要计算一次$C(w+ϵe_j)$，这需要一次完整的前向传播才能得到。假如有一千万个参数，则完整执行一次梯度下降需要一千万+1次前向传播，+1次前向传播是原本计算损失值 $C(w)$的那次。这样的计算量显然不可接受，而反向传播通过链式求导法则，仅需要反向传播一次，并且反向传播与正向传播的计算量相当（反向时采用权重矩阵转置的乘法）。因此反向传播算法可以说是梯度下降在链式法则中的应用。

Q：RNN为什么要基于时间步骤反向传播，直接梯度下降不行吗？

对于RNN训练也是类似的逻辑，通过反向传播来计算梯度。由于RNN具有循环结构，可看作是展开的权重共享的多层神经网络。按照常规的链式求导思路可推导出基于时间步骤反向传播（BPTT）方法，除了有递归结构之外与常规的反向传播无异。与常规反向传播一样，存在梯度消失或梯度爆炸问题。 为了计算方便性和数值稳定性的需要，常使用截断的方法，包括：规则截断和随机截断。截断导致该模型主要侧重于短期影响，而不是长期影响。

反向传播推导

本文以多层感知机为例对反向传播公式进行推导, 但不局限于某种激活函数或损失函数.

先上精简版的图示, 帮助解释:

BP图示

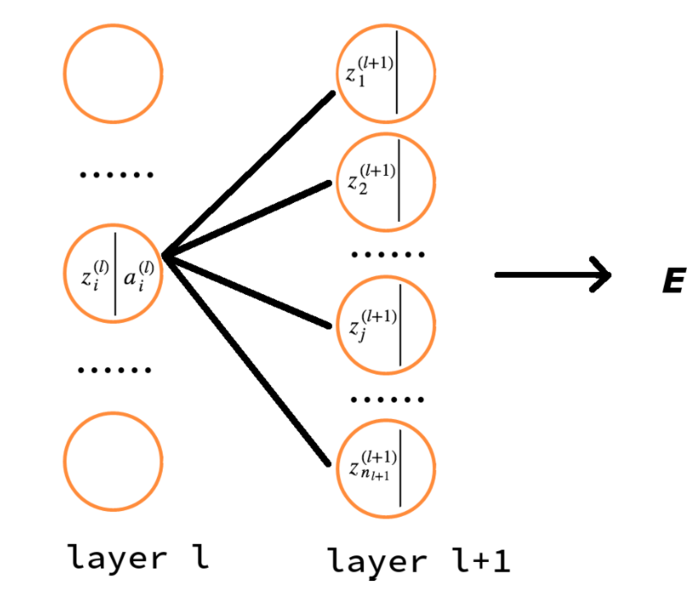
反向传播的目的是更新神经元参数,而神经元参数正是 $z=wx+b$ 中的 $(w,b)$.
对参数的更新为：利用损失值loss对参数求导数, 并沿着负梯度方向进行更新。

$$\begin{gathered} w=w-\eta \mathrm{\nabla }w \\ b=b-\eta \mathrm{\nabla }b \end{gathered}$$

运用链式法则先求误差对当前神经元的线性加权的结果 $z$ 的梯度,再求对当前神经元输入连接的权重 $(w,b)$ 的梯度.

$$\begin{array}{}\text{(1)}& \frac{\partial E}{\partial z_i^l}& =\sum _j[\frac{\partial E}{\partial z_j^{l+1}}\frac{\partial z_j^{l+1}}{\partial a_i^l}\frac{\partial a_i^l}{\partial z_i^l}]\text{(2)}& & =\sum _j[\frac{\partial E}{\partial z_j^{l+1}}{w}_{ji}^{l+1}{\sigma }^{\prime }(z_i^l)]\end{array}$$

其中$\sigma (\cdot )$为激活函数, ${\sigma }^{\prime }(\cdot )$ 为激活函数的导数.
$a_j^{l+1},a_i^l$ 分别代表当前第$l+1$层第$j$个神经元与前一层(第$l$层)第$i$个神经元的激活输出值.

$$\begin{array}{}\text{(3)}& a_i^l=& \sigma (z_l^l)\text{(4)}& z_j^{l+1}=& w_{ji}^{l+1}{a}_i^l+b_j^{l+1}\end{array}$$

注意的是式子和图示中的 $E$ 是单个训练样本的损失, 而式子中的求和符号 $\sum$ 是对应层的神经元求和. 不要和代价损失的求和混淆了(cost function 是对所有训练样本的损失求平均值).

从上式中,你应该能看出来损失对每层神经元的$z_i$的梯度是个从后往前的递推关系式. 即:

$${\delta }_i^l=\sum _j[{\delta }_j^{l+1}{w}_{ji}^{l+1}{\sigma }^{\prime }(z_i^l)]$$

(w,b) 梯度

我们想要的(w,b)的梯度也能够立刻计算出来:
第$l$层的第$i$个神经元与第$l+1$层的第$j$个神经元的权重:

$$\begin{array}{}\text{(5)}& \frac{\partial E}{\partial w_{ji}^{l+1}}& =\frac{\partial E}{\partial z_i^l}\frac{\partial z_i^l}{\partial w_{ji}^{l+1}}={\delta }_j^{l+1}{a}_i^l\text{(6)}& \frac{\partial E}{\partial b_j^{l+1}}& ={\delta }_j^{l+1}\end{array}$$

往前一层(第 i 层)的权重:

$$\begin{array}{}\text{(7)}& \frac{\partial E}{\partial w_{ih}^l}& ={\delta }_i^l{a}_h^{l-1}\text{(8)}& \frac{\partial E}{\partial b_i^l}& ={\delta }_i^l\end{array}$$

就这样, 梯度从后往前一层一层传播计算, 每层的梯度等于后一层的梯度与当前层的局部偏导数的乘积, 这正是链式法则的简单应用。

矩阵乘

对上面的公式稍加变化便能改成矩阵乘法形式:

$$\begin{array}{}\text{(9)}& {\delta }_i^l=\sum _j[{\delta }_j^{l+1}{w}_{ji}^{l+1}{\sigma }^{\prime }(z_i^l)]\text{(10)}& \Rightarrow [{\delta }^{\ell }{]}_{j\times 1}=[(w^{\ell +1}{)}_{k\times j}^T\times ({\delta }^{\ell +1}{)}_{k\times 1}{]}_{j\times 1}\odot {\sigma }^{\prime }(z^{\ell }{)}_{j\times 1}\text{(11)}& [\frac{\partial E}{\partial w^{\ell +1}}{]}_{j\times i}=[{\delta }^{\ell +1}{]}_{j\times 1}\cdot [a^{\ell }{]}_{1\times i}\end{array}$$

其中 $\odot$ 是在反向传播中常用的哈达玛乘积（Hadamard product），对两个相同维度的矩阵按元素相乘得到同维度的输出。

参考

• 神经网络中 BP 算法的原理与 Python 实现源码解析
• BP神经网络——从二次代价函数（Quadratic cost）到交叉熵（cross-entropy cost）代价函数
• 为什么说反向传播算法很高效 · 神经网络与深度学习
• Dive into Deep Learning: 8.7. Backpropagation Through Time
• https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/
• https://github.com/mattm/simple-neural-network/blob/master/neural-network.py