向量检索

近似近邻检索ANNS

Approximate Nearest Neighbor Search (ANNS)

工业界拥有超大规模的数据，往往要求满足低延迟、低成本的向量检索需求，全量计算的精确近邻检索方式难以应用。

近年来各种向量检索算法层出不穷，但是依然面临很多挑战。

检索效果大致对比：HNSW>NSW>Annoy>Ball Tree>KD Tree

KDTree：KD 树沿坐标轴分割数据，用二叉树递归回退搜索，当特征维度较高（>20）时效率很低。

BallTree：BallTree在一系列嵌套的超球面上分割数据，即使用超球面而不是KDTree的超矩形划分区域。

构建BallTree数据结构：将数据递归地划分到由质心 C 和 半径 r 定义的节点上。通过使用三角不等式减少近邻搜索的候选点数。假设q的半径r1，f的半径r2，q-f的距离l，如果r1+r2<l则两圆不相交，f圆内不可能存在近邻点，反之则存在并在f圆内继续搜索。

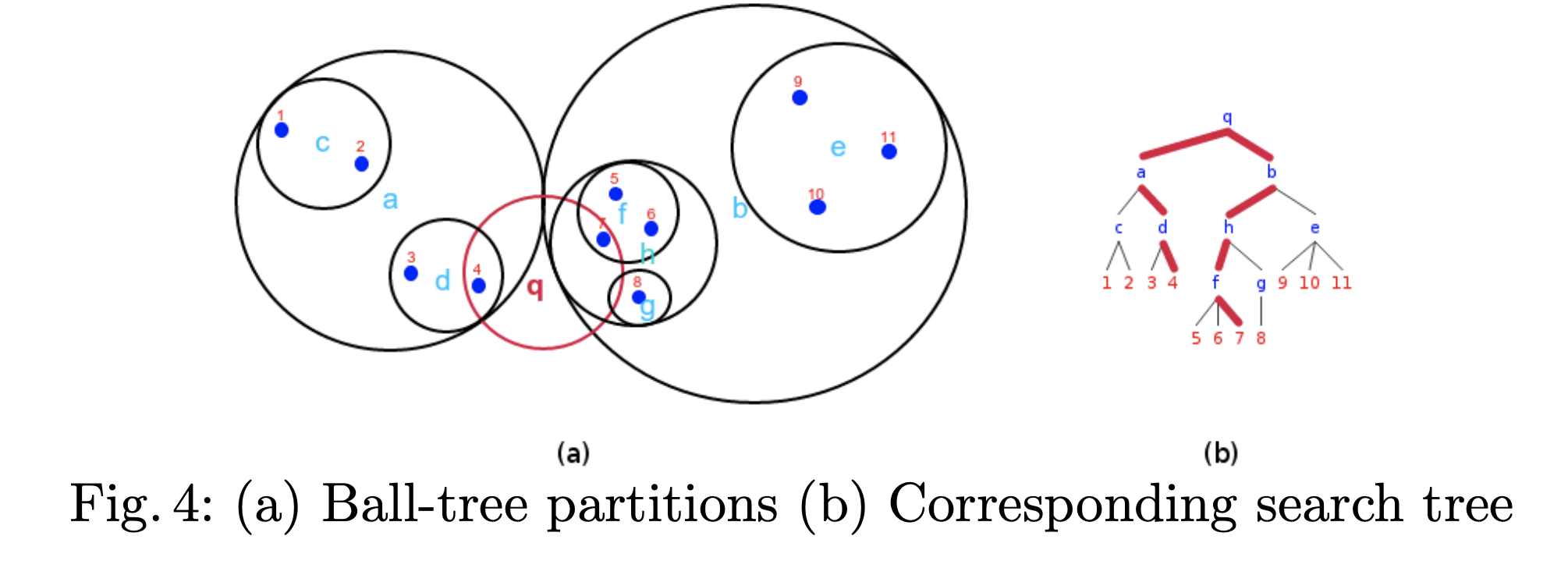
检索

1. 从根节点开始从上至下递归遍历每个可能包含最终近邻的子空间
2. 如果子空间的半径 R(pi)与 r之和大于中心点 pi 到目标点 q 的距离，则圆必相交。接着在满足这样条件的子空间样本点内递归搜索满足条件的点就是我们想要的最近邻点了。

虽然在构建数据结构的花费上大过于KDtree，但是在高维数据上表现很高效。

Annoy

annoy全称“Approximate Nearest Neighbors Oh Yeah”，是一种适合实际应用的快速相似查找算法。Annoy 同样通过建立一个二叉树来使得每个点查找时间复杂度是O(log n)，和kd树不同的是，annoy没有对k维特征进行切分。

annoy的每一次空间划分，可以看作聚类数为2的KMeans过程。收敛后在产生的两个聚类中心连线之间建立一条垂线（图中的黑线），把数据空间划分为两部分。

构造

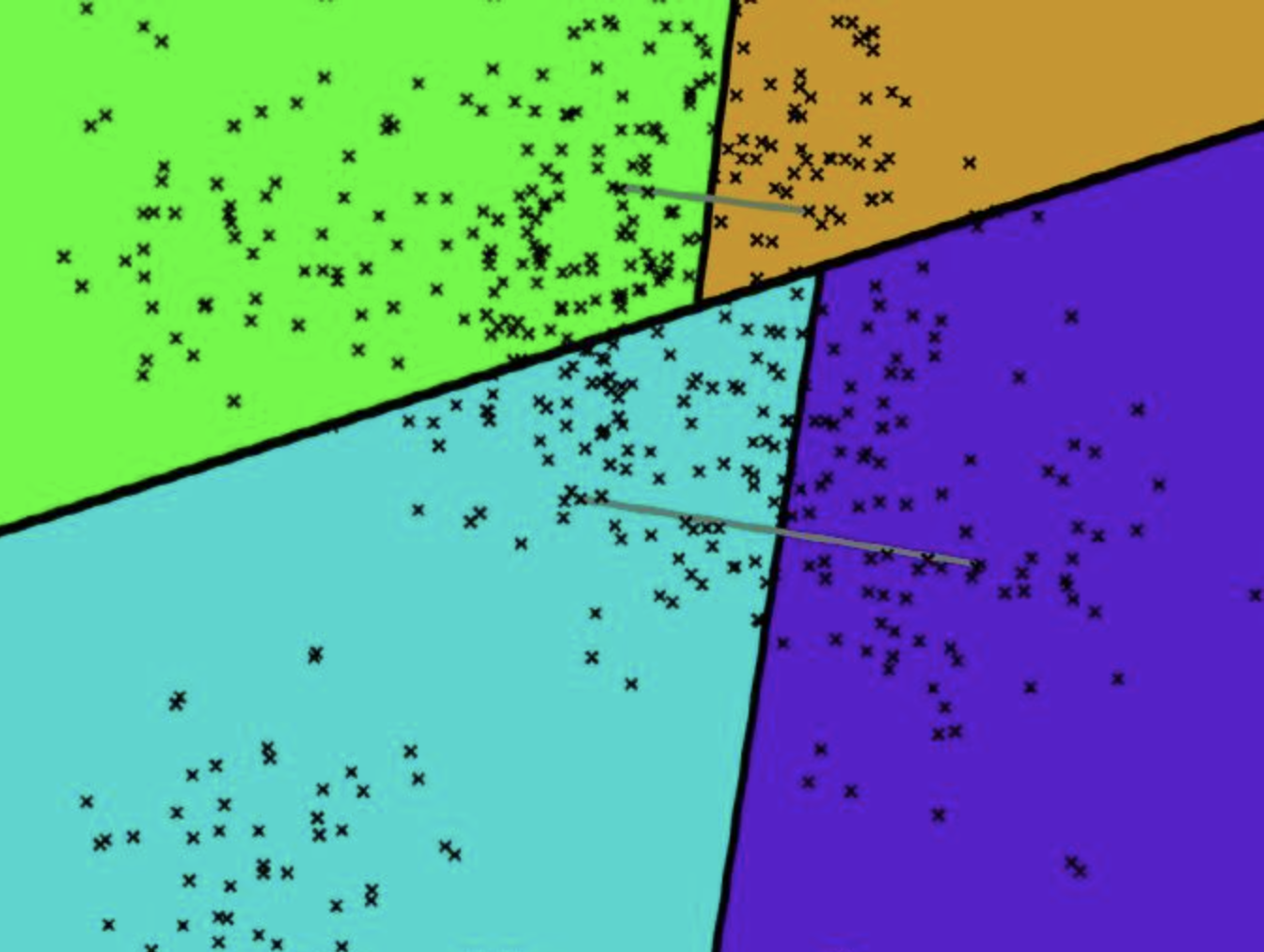
检索

查询过程和kd树类似，先从根向叶子结点递归查找，再向上回溯即可。

特点

annoy接口中一般需要调整的参数有两个：查找返回的topk近邻和树的个数。一般树越多，精准率越高但是对内存的开销也越大，需要权衡取舍。

Annoy 树模型缺点及改进

• 单棵树对向量空间进行硬划分，相近向量可能被划分到不同分支(边界问题)
• 改进：多棵随机树构成森林结果归并，缓解边界问题

NSW

NSW（Navigable Small World graphs）是基于图存储的数据结构

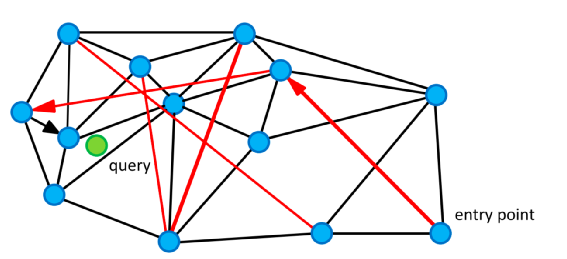
NSW的构图过程：每次在图中插入节点v都寻找m个最近的节点x，在v和x之间建立边的连接。

1. 插入时产生的边称为short-link，用于搜索最近向量。
2. 随着新的距离更近的节点逐渐加入，可能以前的short-link不再是距离最近的k个，这个时候short-link变成了long-link（“高速公路”，图中的红线），在搜索初期能够提高搜索效率。

检索

随机选择一个点（entry point）作为当前顶点加入结果集合，计算q到当前顶点的朋友列表的每个顶点的距离，然后选择具有最小距离的顶点。如果这个顶点距离大于结果集合中的最大距离，则算法停止；否则加入集合，或者集合已满时替换其中的最大距离点。将该点作为当前点，继续迭代。

越早插入的点冗余边越多，检索效率越低，针对这一点，后提出的HNSW优化了查询效率。

HNSW 紧密图

Hierarchical NSW 加入了跳跃表结构。最底层是所有数据点，每一个点都有50%概率进入上一层的有序链表。这样可以保证表层是“高速通道”，底层是精细查找。

skip list 为了在原始的链表进行快速检索，增加了更高的稀疏层，先从稀疏层查询起，符合条件的再逐级靠下向稠密层查询。图示如下（点击 来源图片wikipedia 查看动图）：

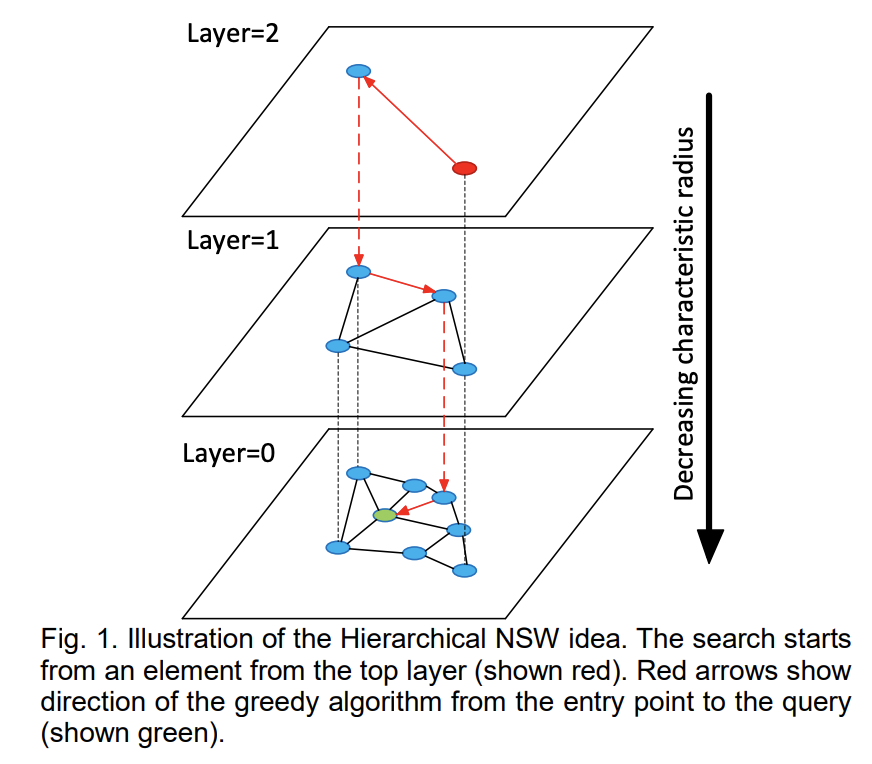
原理

• “六度空间”-任意两个人都可以通过6个熟人连接
• 在NSW中，任意两个节点可以通过O(log(N))个节点连通
• 通过“跳表”将NSW中节点的度从O(log(N))降低到O(1)

构造

向上节点数依次减少，遵循指数衰减概率分布，\(p=\exp(-m_L)\)

建图时新加入的节点由公式得出该点最高投影到第几层：\(l← ⌊-\ln(U[0,1])\cdot m_L⌋\)，将该节点加入到第 \(0\sim l\) 层，平均层数也是一个常数：\(E[l+1]=E\left[-\ln (U[0,1]) \cdot m_{L}\right]+1=m_{L}+1\)

其中 \(m_L\) 是一个固定的超参数。期望的计算方法如下：

\[\begin{align} \int \ln xdx &= x\ln x-\int x\ d\ln x = x\ln x-\int x\cdot {1\over x}dx \\ &=x\ln x-x+C \\ E[-\ln x] &= [x-x\ln x]|_0^1 = 1, \quad 其中\ x\sim U[0,1] \end{align} \]

检索

• 从高层开始逐级向下搜索，在每一层找到距离最近的k个节点与插入节点建立边，每一层的搜索算法和NSW一样。
• 下一层的开始搜索节点则为上一层搜索的近邻点

HNSW 将 NSW 的计算复杂度由多重对数复杂度降到了对数复杂度。

近邻图算法可以无需预训练，实时的增删节点，此外在保证非常好的召回率的情况下检索性能也非常好，不过近邻图的问题就是构图时要全图检索，很难分布式化。

IVFPQ 乘积量化

IVFPQ = PQ + 倒排索引，其中PQ是product-quantization(乘积量化)。

乘积量化（PQ）算法由法国INRIA实验室提出，最初为了加快图像的检索速度，论文：Product Quantization for Nearest Neighbor Search。

基本原理：

• 向量内积可以因式分解为“向量段”内积之和
• 利用k-means质心近似表示“向量段”
• 通过计算量化后距离实现任意向量快速计算近似内积

构造

量化过程如下图所示，通过空间切分，将高维的向量通过预处理压缩到低维度：

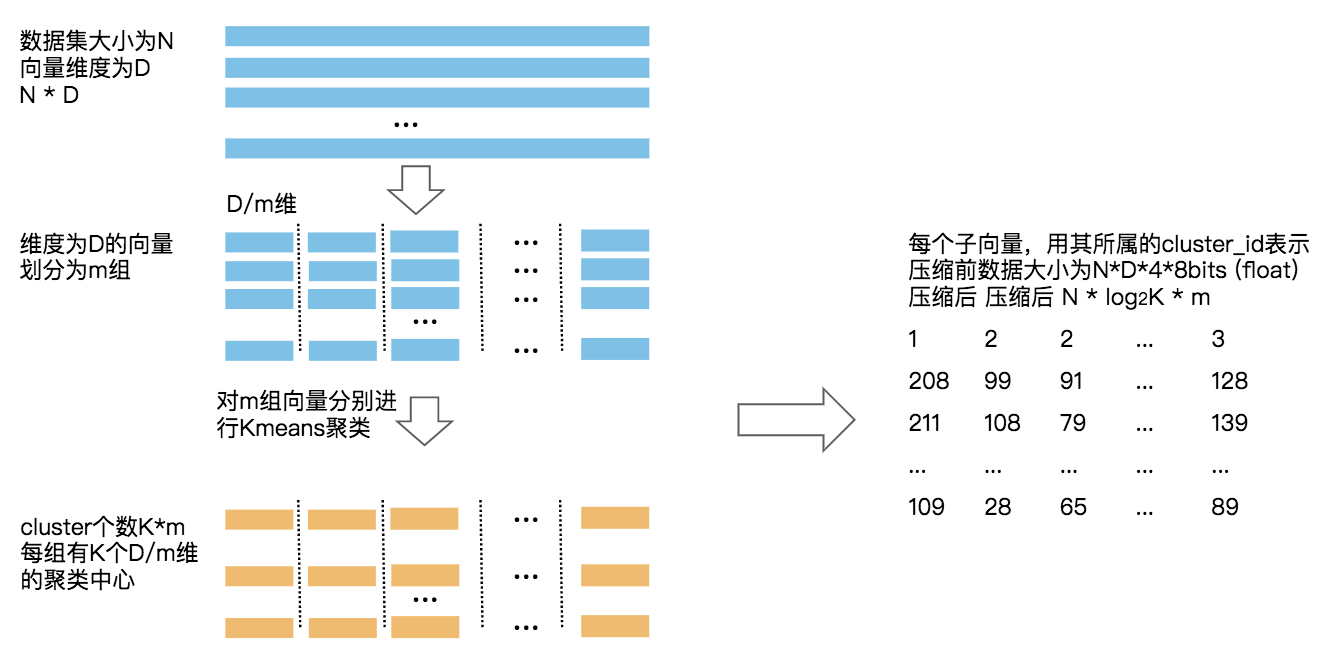
检索

对一个新的查询向量q，计算与库内向量v的距离：对q按相同方式量化，分段与每个聚类中心计算距离，得到距离矩阵M，用v压缩后的向量与M做查询计算得到q与每个分段的距离，对分段距离求和作为整体的近似距离。

和全量计算相比，PQ检索算法仅仅降低了维度，在检索时仍然做全量查询，再取top向量作为检索结果，效率依然很低。

改进思路：可以从q分段量化后类簇的交集中取top K，由于量化导致类簇不精确，可以在原始向量上聚类，再在1或多个类簇内做量化检索。这正是IVFPQ的改进思路，类似于倒排、二叉树的思想。

IVFPQ： 聚类向量倒排 + 残差 + 乘积量化

构造

1. 预先对库内原始向量聚类，记录向量倒排结果，用于在线检索时缩小遍历空间。
2. 对每一聚类的向量进行PQ量化，这里增加一个优化点：不再用原始向量，而是用原始向量减去这个聚类中心向量的残差进行量化，这样召回率更高。

检索

1. 在线查询q先和每一类的中心比较，挑选距离较近的m个类，m越大速度越慢但是召回越高
2. 从这个m个类中进行PQ查询

缺点：

1. 由于要对原始向量进行聚类，没法做到从0开始插入数据，即不支持热插入。
2. 聚类后加入的向量若发生离群（离任何类中心都较远或者距离差不多），那么这些向量的召回会很低
3. 如果原始向量分布很均匀，那么聚类效果很差，导致最终的召回率很低

技术选型

公共测试集： ann-benchmarks.com、glove-100

评测指标：效果指标:召回率；效率指标:QPS，建库时间。

相同召回率下QPS: hnswlib >> faiss-ivfpq ≈ annoy

相同召回率下建库时间: faiss-ivfpq < annoy < hnsw

内存占用：faiss-ivfpq < annoy ≈ hnsw

其它考虑点：

• faiss-ivfpq能变成特殊的求交表达式，更容易和倒排求交兼容
• hnsw支持热插入，时效性强

检索工具

FAISS

FAISS 是 Facebook AI Research 开发的用于稠密向量的相似性搜索和聚类的高效运算库。

• 包含了任何大小的向量集合里进行搜索的算法，包含了无法被完全读入内存空间的向量集合。
• 采用C++编写，同时提供了Python接口，部分算法同时支持CPU、GPU计算。
• 仅公开了单机版，不支持分布式。

支持的近邻检索算法包括：HNSW、LSH、Scalar quantizer (SQ)、Product quantizer (PQ)、IVFADC（IVFPQ）等，见 Faiss indexes · faiss Wiki

安装faiss-gpu：官方的pytorch channel不提供cudatoolkit=8.0了，如果需要使用cuda8.0的，或者其它特定版本，可以先从anaconda channel安装cudatoolkit，然后再从pytorch channel安装faiss-gpu会自动选择安装和对应cudatoolkit配套的版本。

conda install cudatoolkit=8.0 -c anaconda
conda install faiss-gpu -c pytorch

如遇网络连接问题，可到https://anaconda.org/ 搜索下载对应的压缩包，直接install file。

faiss的用法：可参考 知乎

faiss出现 TypeError: in method 'fvec_renorm_L2', argument 3 of type 'float *'

原因：faiss在加载和处理embedding矩阵的时候限制了类型为float32，而自己读入embedding文件创建numpy ndarrary时默认大小是float64导致的。检查my_numpy_ndarray.dtype类型，转换类型：new_array = my_numpy_ndarray.astype('float32')

hnswlib

nmslib/hnswlib: Header-only C++/python library for fast approximate nearest neighbors

Header-only C++ HNSW implementation with python bindings.

支持的距离度量方式如下:

Distance	parameter	Equation
Squared L2	'l2'	d = sum((Ai-Bi)^2)
Inner product	'ip'	d = 1.0 - sum(Ai*Bi)
Cosine similarity	'cosine'	d = 1.0 - sum(Ai*Bi) / sqrt(sum(Ai*Ai) * sum(Bi*Bi))

一般HNSW采用欧式距离构建检索图，在点乘距离的数据集上效果差。

注意：点乘（inner product）不是一个真正的距离度量方式，因为一个向量与其它向量之间的点积结果可能比自身的点积还小。并且不满足三角不等式 ，距离比较没有传递性，因此不满足距离的定义。而余弦距离也同样不满足三角不等式，不是真正的距离度量，但优势在于取值范围不受向量维度、绝对值的影响。如果对向量归一化，那么点乘、余弦、欧式距离则可以实现统一。

业界其它

业界开源的基于faiss、SPTAG等实现的支持分布式、海量数据的检索工具有：

• Milvus，来自国内Zilliz公司。
• 京东 Vearch。

非开源，服务于内部众多产品线的有：

• ElasticFaiss 腾讯基于faiss实现的分布式向量相似性搜索服务，提供类似ElasticSearch的API。
• 阿里达摩院 - Proxima & 蚂蚁金服- ZSearch。

facebook的faiss、微软的SPTAG属于开发库，而Milvus、vearch等属于包装后的开箱即用的工具，便于在生产环境中应用。

参考

• Approximate nearest neighbor algorithm based on navigable small world graphs
• Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs
• 向量快速检索方法总结—KDtree/Balltree/Annoy/NSW/HNSW
• 向量检索简述
• 乘积量化（Product Quantization）
• 几款多模态向量检索引擎：Faiss 、milvus、Proxima、vearch、Jina等 - 知乎
• 【向量检索研究系列】产品介绍