排序算法总结
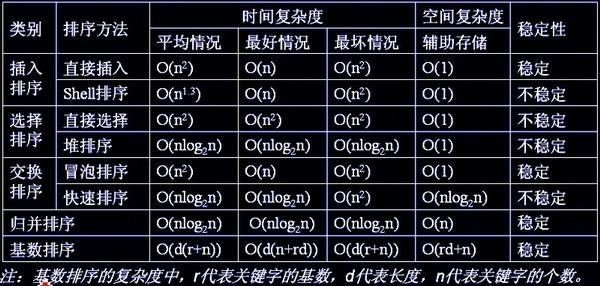
一篇很好的讲8大排序的博客
选择排序 (不稳定)
- 选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择中,如果当前元素比一个元素大,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法。
堆排序 (不稳定)
- 堆的结构是节点i的孩子为 2i 和 2i+1 节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n的序列,堆排序的过程,首先要根据floyd算法建堆,因此要从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n/2-1, n/2-2,...1这些个父节点选择元素时,就会破坏稳定性。有可能第n/2个父节点交换把后面一个元素交换过去了,而第n/2-1个父节点把后面一个相同的元素没有交换,那么这2个相同的元素之间的稳定性就被破坏了。所以,堆排序不是稳定的排序算法。
- eg:{5A,6,5B,7,8} --> {8,7,5B,5A,6} ,两个5的顺序颠倒了。
插入排序 (稳定)
- 插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。插入调用有序序列的search操作,该操作返回的是第一个大于该元素的位置,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
希尔排序 (不稳定)
- 希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小,插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比o(n^2)好一些。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
冒泡排序 (稳定)
- 冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,我想你是不会再无聊地把他们俩交换一下的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
快速排序 (不稳定)
- 快速排序有两个方向,当a[i] <= a[center_index],左边的i下标一直往右走,其中center_index是中枢元素的数组下标,一般取为数组第0个元素。
- 当a[j] > a[center_index],右边的j下标一直往左走。如果i和j都走不动了,i <= j,交换a[i] 和 a[j],重复上面的过程,直到i>j。交换a[j]和a[center_index],完成一趟快速排序。在中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱.
- 比如序列为 5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j]交换的时刻。
归并排序 (稳定)
- 归并排序是把序列递归地分成短序列,递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2个元素如果大小相等也没有人故意交换,这不会破坏稳定性。那么,在短的有序序列合并的过程中,稳定是是否受到破坏?没有,合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,这样就保证了稳定性。所以,归并排序也是稳定的排序算法。
基数排序 (稳定)
- 基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序,最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以其是稳定的排序算法。
1.快速排序
#include<iostream>
#include<vector>
using namespace std;
void swap(int &p, int &q)
{
int temp;
temp = p;
p = q;
q = temp;
}
int partition(vector<int>&array, int lo, int hi){
swap(array[lo], array[lo + rand() % (hi - lo + 1)]);//产生[lo,hi]之间的一个随机数
int pivot = array[lo];
while (lo < hi){
//swap
while ((lo < hi) && pivot <= array[hi])
{
hi--;
}
//array[lo] = array[hi];
swap(array[lo], array[hi]);
while ((lo < hi) && pivot >= array[lo])
{
lo++;
}
//array[hi] = array[lo];
swap(array[lo], array[hi]);
}
//array[lo] = pivot;
return lo;
}
void quicksort(vector<int>&array, int lo, int hi){
if (hi - lo < 1)return;
int mi = partition(array, lo, hi);
quicksort(array, lo, mi-1);
quicksort(array, mi + 1, hi);
}
int partition(vector<int>&array, int lo, int hi){
int pivot = array[lo];
while (lo < hi){
while (lo < hi&&pivot <= array[hi])hi--;
swap(array[lo], array[hi]);
while (lo < hi&&pivot >= array[lo])lo++;
swap(array[lo], array[hi]);
}
return lo;
}
/**使用栈的非递归快速排序**/
void quicksort2(vector<int> &vec, int low, int high){
stack<int> st;
if (low<high){
int mid = partition(vec, low, high);
if (low<mid - 1){
st.push(low);
st.push(mid - 1);
}
if (mid + 1<high){
st.push(mid + 1);
st.push(high);
}
//其实就是用栈保存每一个待排序子串的首尾元素下标,下一次while循环时取出这个范围,对这段子序列进行partition操作
while (!st.empty()){
int q = st.top();
st.pop();
int p = st.top();
st.pop();
mid = partition(vec, p, q);
if (p<mid - 1){
st.push(p);
st.push(mid - 1);
}
if (mid + 1<q){
st.push(mid + 1);
st.push(q);
}
}
}
}
2.归并排序
void merge(vector<int>&input, int left, int right, int mid, vector<int>&temp){
int i = left;
int j = mid+1;
int t = 0;
while (i<=mid&&j<=right){
if (input[i] <= input[j]){
temp[t++] = input[i++];
}
else{
temp[t++] = input[j++];
}
}
while (i <= mid){
temp[t++] = input[i++];
}
while (j <= right){
temp[t++] = input[j++];
}
t = 0;
while (left <= right){
input[left++] = temp[t++];
}
}
void mergesort(vector<int>&input, int left, int right, vector<int>&temp){
if (left < right){
int mid = (left + right) / 2;
mergesort(input, left, mid, temp);
mergesort(input, mid + 1, right, temp);
merge(input, left, right, mid, temp);
}
}
3.堆排序
/*
* (最大)堆的向下调整算法
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。数组是按层编号的。
* 其中,N为数组下标索引值,如数组中第1个数对应的N为0。
*
* 参数说明:
* a -- 待排序的数组
* start -- 被下调节点的起始位置(一般为0,表示从第1个开始)
* end -- 截至范围(一般为数组中最后一个元素的索引)
*/
void maxheap_down(int a[], int start, int end)
{
int c = start; // 当前(current)节点的位置
int l = 2*c + 1; // 左(left)孩子的位置
int tmp = a[c]; // 当前(current)节点的大小
for (; l <= end; c=l,l=2*l+1)
{
// "l"是左孩子,"l+1"是右孩子
if ( l < end && a[l] < a[l+1])
l++; // 左右两孩子中选择较大者,即m_heap[l+1]
if (tmp >= a[l])
break; // 调整结束
else // 交换值
{
a[c] = a[l];
a[l]= tmp;
}
}
}
/*
* 堆排序(从小到大)
*
* 参数说明:
* a -- 待排序的数组
* n -- 数组的长度
*/
void heap_sort_asc(int a[], int n)
{
int i;
// 从(n/2-1) --> 0逐次遍历。遍历之后,得到的数组实际上是一个(最大)二叉堆。从下到上,从左到右遍历父节点调整
for (i = n / 2 - 1; i >= 0; i--)
maxheap_down(a, i, n-1);
// 从最后一个元素开始对序列进行调整,不断的缩小调整的范围直到第一个元素
for (i = n - 1; i > 0; i--)
{
// 交换a[0]和a[i]。交换后,a[i]是a[0...i]中最大的。
swap(a[0], a[i]);
// 调整a[0...i-1],使得a[0...i-1]仍然是一个最大堆。
// 即,保证a[i-1]是a[0...i-1]中的最大值。//下面一条语句start=0是因为第一个父节点改变了值,要重新调整为最大堆
maxheap_down(a, 0, i-1);
}
}
/ brief /
void makeheap_down(vector<int>&array, int start, int end){
int c = start;//c是当前要下滤的节点
for (int i = 2 * start + 1; i <= end; c = i, i = 2 * i + 1){
if (i<end&&array[i] < array[i + 1])i++;//i<end不能漏,不然i=end;i+1超出范围
if (array[c] >= array[i])break;
else{
swap(array[c], array[i]);
}
}
}
/*堆排序*/
void maxheap_sort(vector<int>&a, int n){
//第一个for循环构建最大堆,n为向量长度
for (int i = n / 2 - 1; i >= 0; i--)
makeheap_down(a, i, n-1);
//第二个for循环用来排序
for (int i = n-1; i>0; i--){
swap(a[0], a[i]);
makeheap_down(a, 0, i-1);//再次调整为最大堆 ,i不能=0
}
}
4.选择排序
void select_sort(vector<int>&a){
for (int i = 0; i < a.size()-1; i++){
int min_index = i;
for (int j = i+1; j < a.size(); j++){
if (a[j] < a[min_index]){
min_index = j;
}
}
if (min_index!=i)swap(a[i], a[min_index]);
}
}
5.冒泡排序
void bubble_sort(vector<int>&a){
for (int i = 0; i < a.size()-1; i++){
for (int j = 0; j < a.size()-1-i; j++){
if (a[j] > a[j + 1]){
//swap(a[j], a[j + 1]);
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
}
}
}
}
6.插入排序
void insert_sort(vector<int>&a){
for (int i = 1; i < a.size(); i++){
int j = i;
while (j>0 && a[j] < a[j - 1]){
swap(a[j], a[j - 1]);
j--;
}
}
}
7.桶排序和基数排序
void bucketSort(vector<int>&input,int max){
vector<int>bucket(max, 0);//max是要排序数组中的最大值+1
for (int i = 0; i < input.size(); i++){
bucket[input[i]]++;
}
for (int i = 0,j=0; i < max; i++){
while ((bucket[i]--)> 0){//可以排序重复数字
input[j++] = i;
}
}
}
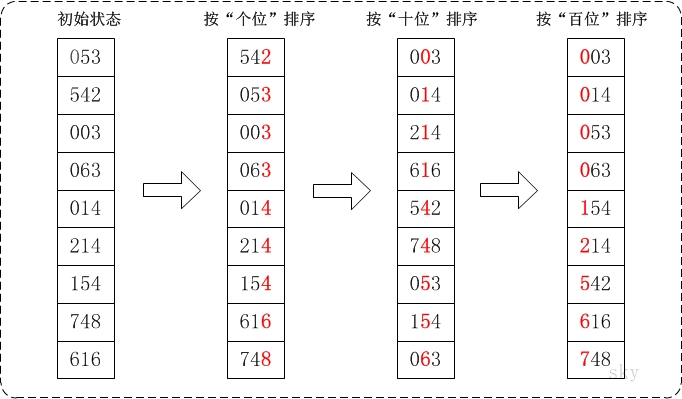
基数排序补充:基数排序(Radix Sort)是桶排序的扩展,它的基本思想是:将整数按位数切割成不同的数字,然后按每个位数分别比较。
具体做法是:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
/*
* 获取数组a中最大值
*
* 参数说明:
* a -- 数组
* n -- 数组长度
*/
int get_max(int a[], int n)
{
int i, max;
max = a[0];
for (i = 1; i < n; i++)
if (a[i] > max)
max = a[i];
return max;
}
/*
* 对数组按照"某个位数"进行排序(桶排序)
*
* 参数说明:
* a -- 数组
* n -- 数组长度
* exp -- 指数。对数组a按照该指数进行排序。
*
* 例如,对于数组a={50, 3, 542, 745, 2014, 154, 63, 616};
* (01) 当exp=1表示按照"个位"对数组a进行排序
* (02) 当exp=10表示按照"十位"对数组a进行排序
* (03) 当exp=100表示按照"百位"对数组a进行排序
* ...
*/
void count_sort(int a[], int n, int exp)
{
int output[n]; // 存储"被排序数据"的临时数组
int i, buckets[10] = {0};
// 将数据出现的次数存储在buckets[]中
for (i = 0; i < n; i++)
buckets[ (a[i]/exp)%10 ]++;
// 更改buckets[i]。目的是让更改后的buckets[i]的值,是该数据在output[]中的位置。
for (i = 1; i < 10; i++)
buckets[i] += buckets[i - 1];
// 将数据存储到临时数组output[]中
for (i = n - 1; i >= 0; i--)
{
output[buckets[ (a[i]/exp)%10 ] - 1] = a[i];
buckets[ (a[i]/exp)%10 ]--;
}
// 将排序好的数据赋值给a[]
for (i = 0; i < n; i++)
a[i] = output[i];
}
/*
* 基数排序
*
* 参数说明:
* a -- 数组
* n -- 数组长度
*/
void radix_sort(int a[], int n)
{
int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10;...
int max = get_max(a, n); // 数组a中的最大值
// 从个位开始,对数组a按"指数"进行排序
for (exp = 1; max/exp > 0; exp *= 10)
count_sort(a, n, exp);
}
#include <stdio.h> #include <algorithm> #include <map> #include <iostream> #include <vector> using namespace std; //自己写的实现 /* * 快速排序 * 平均时间复杂度O(nlogn):对应的情况是每次递归结束后,(i-left)约等于(right-i),两边的数的数量相同,类似二分,所以递归深度logn,总复杂度O(nlogn) * 最坏时间复杂度O(n*n):对应的情况是每次递归结束后,i等于left或者i等于right,每层递归只能排序一个数,这样的话递归深度就是n,总复杂度O(n*n),对已经排序好的数组再次排序就是这种情况 * 为什么要右边的哨兵先行: 如果选取最左边的数nums[left]作为基准数,那么先从右边开始可保证i,j在相遇时,相遇数是小于基准数的,交换之后base所在位置的左边都小于base。但先从左边开始,相遇数是大于基准数的,无法满足base左边的数都小于它。所以进行扫描,要从基准数的对面开始 * 稳定性:快速排序是不稳定排序,它可能会交换两个值相同的元素。比如序列为 5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j]交换的时刻。 */ class QuickSort { public: void quickSort(vector<int>& nums, int left,int right) { if(left >= right) return; int i=left, j=right; int base = nums[left]; while(i < j) { while(nums[j]>=base && i<j) j--; while(nums[i]<=base && i<j) i++; if(i < j) { swap(nums[i], nums[j]); } } swap(nums[i], nums[left]); quickSort(nums, left,i-1); quickSort(nums, i+1,right); } vector<int> sortArray(vector<int>& nums) { quickSort(nums, 0, nums.size()-1); return nums; } }; /* * 归并排序 * 平均时间复杂度和最坏时间复杂度都是O(nlogn) * 稳定性:稳定排序 * 缺点:需要辅助数组 */ class MergeSort { public: void merge(vector<int>& nums, int left, int right, int mid) { vector<int> temp(right-left+1); int i = left, j = mid+1, t = 0; while (i<=mid && j<=right){ if (nums[i] <= nums[j]) temp[t++] = nums[i++]; else temp[t++] = nums[j++]; } while (i <= mid){ temp[t++] = nums[i++]; } while (j <= right){ temp[t++] = nums[j++]; } t = 0; while (left <= right){ nums[left++] = temp[t++]; } } void mergeSort(vector<int>& nums, int left, int right){ if (left < right){ int mid = (left + right) / 2; mergeSort(nums, left, mid); mergeSort(nums, mid + 1, right); merge(nums, left, right, mid); } } vector<int> sortArray(vector<int>& nums) { mergeSort(nums, 0, nums.size()-1); return nums; } }; /* * 堆排序 * 稳定性:不稳定 */ class Heap { private: int heap[10005]; int size = 0; public: int getSize() { return size; } void siftDown(int i) { while(true) { int t = i; if(i*2 <= size) { if(heap[i*2] < heap[i]) t = i*2; } if(i*2+1 <= size) { if(heap[i*2+1] < heap[t]) t = i*2+1; } if(t != i) { swap(heap[t], heap[i]); i = t; } else { break; } } } void siftUp(int i) { while (true) { if (i == 1) break; if (heap[i/2] > heap[i]) { swap(heap[i/2], heap[i]); i /= 2; } else { break; } } } void pop () { heap[1] = heap[size--]; siftDown(1); } void add (int num) { heap[++size] = num; siftUp(size); } int top() { return heap[1]; } }; class HeapSort { public: int findKthLargest(vector<int>& nums, int k) { Heap hp; for(auto x: nums) { hp.add(x); if (hp.getSize() > k) hp.pop(); } return hp.top(); } }; int main() { Solution s; vector<int> v; for(int i=1; i<=50000; ++i) v.push_back(i); cout<<1<<endl; vector<int> nums = s.sortArray(v); // for(int i=0; i<nums.size(); ++i) // cout<<nums[i]<<endl; }




