bzoj3995[SDOI2015]道路修建
http://www.lydsy.com/JudgeOnline/problem.php?id=3995
线段树维护连通性。
我们发现,对于一个区间[L,R],我们只需要知道(1,L),(2,L),(1,R)和(2,R)这4个点的之间的连通情况即可。
我们在线段树中,假设当前节点的表示的区间的为[L,R],我们需要知道(1,L),(2,L),(1,R)和(2,R)这4个点的之间的连通情况,但是为了方便,我们记了(1,L),(2,L),(1,R+1)和(2,R+1)这4个点的连通情况。
每个节点记住5种连通情况:
1:
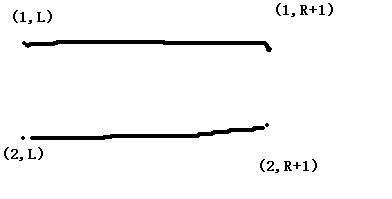
2:

3:
 或
或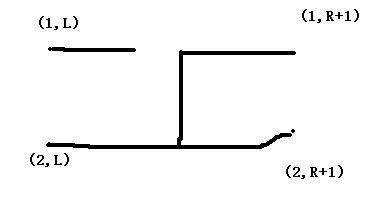
4:
 或
或
5:
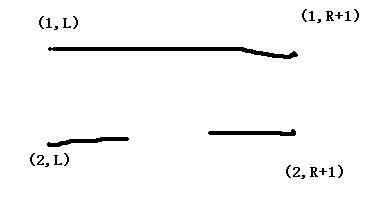 或
或
这样分类的好处是合并的时候比较简单。
合并的时候只有17种是合法的,一一打表即可。

#include<cstdio> #include<cstdlib> #include<iostream> #include<fstream> #include<algorithm> #include<cstring> #include<string> #include<cmath> #include<queue> #include<stack> #include<map> #include<utility> #include<set> #include<bitset> #include<vector> #include<functional> #include<deque> #include<cctype> #include<climits> #include<complex> //#include<bits/stdc++.h>适用于CF,UOJ,但不适用于poj using namespace std; typedef long long LL; typedef double DB; typedef pair<int,int> PII; typedef complex<DB> CP; #define mmst(a,v) memset(a,v,sizeof(a)) #define mmcy(a,b) memcpy(a,b,sizeof(a)) #define fill(a,l,r,v) fill(a+l,a+r+1,v) #define re(i,a,b) for(i=(a);i<=(b);i++) #define red(i,a,b) for(i=(a);i>=(b);i--) #define ire(i,x) for(typedef(x.begin()) i=x.begin();i!=x.end();i++) #define fi first #define se second #define m_p(a,b) make_pair(a,b) #define p_b(a) push_back(a) #define SF scanf #define PF printf #define two(k) (1<<(k)) template<class T>inline T sqr(T x){return x*x;} template<class T>inline void upmin(T &t,T tmp){if(t>tmp)t=tmp;} template<class T>inline void upmax(T &t,T tmp){if(t<tmp)t=tmp;} inline int sgn(DB x){if(abs(x)<1e-9)return 0;return(x>0)?1:-1;} const DB Pi=acos(-1.0); int gint() { int res=0;bool neg=0;char z; for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar()); if(z==EOF)return 0; if(z=='-'){neg=1;z=getchar();} for(;z!=EOF && isdigit(z);res=res*10+z-'0',z=getchar()); return (neg)?-res:res; } LL gll() { LL res=0;bool neg=0;char z; for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar()); if(z==EOF)return 0; if(z=='-'){neg=1;z=getchar();} for(;z!=EOF && isdigit(z);res=res*10+z-'0',z=getchar()); return (neg)?-res:res; } const int maxN=60000; const int INF=0x3f3f3f3f; int N,Q; int A[maxN+10][3]; struct Tnode { int X[6]; int& operator [](int i){return X[i];} }; const int magic[20][5]= { {1,1,1}, {1,2,2}, {1,3,3}, {1,4,4}, {1,5,5}, {2,1,2}, {2,3,2}, {2,5,4}, {3,1,3}, {3,3,3}, {3,5,5}, {4,1,4}, {4,2,2}, {4,4,4}, {5,1,5}, {5,2,3}, {5,4,5}, }; Tnode operator +(Tnode L,Tnode R) { int i;Tnode res; mmst(res.X,0x3f); re(i,0,17-1)upmin(res[magic[i][2]],L[magic[i][0]]+R[magic[i][1]]); return res; } Tnode T[4*maxN+1000]; Tnode calc(int s) { Tnode res; res[1]=A[s][1]+A[s][2]; res[2]=A[s][1]+A[s][2]+A[s][0]+A[s+1][0]-max(max(A[s][1],A[s][2]),max(A[s][0],A[s+1][0])); res[3]=A[s+1][0]+min(A[s][1],A[s][2]); res[4]=A[s][0]+min(A[s][1],A[s][2]); res[5]=min(A[s][1],A[s][2]); return res; } void build(int rt,int l,int r) { if(l==r){T[rt]=calc(l);return;} int mid=(l+r)>>1; build(rt<<1,l,mid); build(rt<<1|1,mid+1,r); T[rt]=T[rt<<1]+T[rt<<1|1]; } void change(int rt,int l,int r,int x) { if(l==r){T[rt]=calc(l);return;} int mid=(l+r)>>1; if(x<=mid) change(rt<<1,l,mid,x); else change(rt<<1|1,mid+1,r,x); T[rt]=T[rt<<1]+T[rt<<1|1]; } Tnode ask(int rt,int l,int r,int x,int y) { if(x<=l && r<=y) return T[rt]; int mid=(l+r)>>1; if(y<=mid) return ask(rt<<1,l,mid,x,y); if(mid+1<=x) return ask(rt<<1|1,mid+1,r,x,y); return ask(rt<<1,l,mid,x,y)+ask(rt<<1|1,mid+1,r,x,y); } int main() { freopen("road.in","r",stdin); freopen("road.out","w",stdout); int i; N=gint();Q=gint(); re(i,1,N-1)A[i][1]=gint(); re(i,1,N-1)A[i][2]=gint(); re(i,1,N)A[i][0]=gint(); build(1,1,N-1); while(Q--) { char type=getchar();while(type!='C' && type!='Q')type=getchar(); if(type=='C') { int x0=gint(),y0=gint(),x1=gint(),y1=gint(),w=gint(); if(x0==x1) { A[min(y0,y1)][x0]=w; change(1,1,N-1,min(y0,y1)); } else { A[y0][0]=w; if(y0!=1)change(1,1,N-1,y0-1); if(y0!=N)change(1,1,N-1,y0); } } else { int l=gint(),r=gint(); if(l==r) PF("%d\n",A[l][0]); else { Tnode ans=ask(1,1,N-1,l,r-1); PF("%d\n",ans[2]); } } } return 0; }




