2015.8.28 字符串
【题目描述】
在一个n行m列的矩阵,每个格子都有一个大写的英文字母。你需要从左上角格子走到右下角格子,你每一次只能从当前格子往下走一步或者往右走一步,当然不能走出矩阵。给出由大写英文字母构成的字符串s[1..n+m-1]和t[1..n+m-1],这两个字符串的长度都是n+m-1,其中s不等于t。对于这样的一个矩阵A,如果存在两条路径,使得路径经过的字符分别构成字符串s和字符串t。那么矩阵A是“好矩阵”。问总共有多少个“好矩阵”,答案模1000000009。
【输入格式】str.in
多组测试数据。
第一行,一个整数G,表示有G组测试数据。1 <=G <=4。
每组测试数据格式:
第一行,n和m。1 <= n,m<= 8。
第二行,字符串s,长度是n+m-1,都是大写英文字母。
第三行,字符串t,长度是n+m-1,都是大写英文字母。
【输出格式】str.out
一个整数。
【输入样例】
4
2 2
ABD
ACD
2 3
ABD
ABC
3 4
ABCDDE
ACCBDE
3 2
LLFF
LLWF
【输出样例】
2
0
1899302
52
插头DP
其实只要知道怎么记状态就很容易写了。
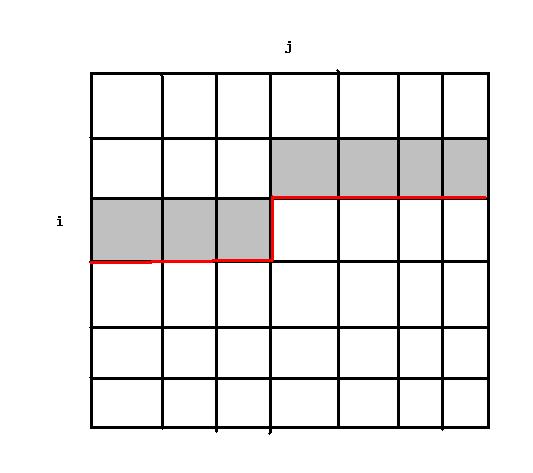
如图,记$F[i][j][state1][state2]$表示做到第$i$行第$j$列的格子(即如图红色轮廓线上方的部分已经完成),$state1$是一个8位二进制数,如果$state1$的第$k$位为1表示s字符串能到达第$k$列与红色轮廓线接触的格子(即如图第$k$列的灰色格子),0则表示s字符串不能到达第$k$列与红色轮廓线接触的格子;$state2$也是一个8位二进制数,与$state1$类似,如果$state2$的第$k$位为1表示t字符串能到达第$k$列与红色轮廓线接触的格子(即如图第$k$列的灰色格子),0则表示t字符串不能到达第$k$列与红色轮廓线接触的格子。
然后我们可以从A到Z枚举下一个位置(i,j+1)是什么,然后就可以转移到F[i][j+1]了。
换行的时候特别处理一下即可。
时间复杂度$O(26NM2^{2M})$

#include<cstdio> #include<cstdlib> #include<iostream> #include<fstream> #include<algorithm> #include<cstring> #include<string> #include<cmath> #include<queue> #include<stack> #include<map> #include<utility> #include<set> #include<bitset> #include<vector> #include<functional> #include<deque> #include<cctype> #include<climits> #include<complex> //#include<bits/stdc++.h>适用于CF,UOJ,但不适用于poj using namespace std; typedef long long LL; typedef double DB; typedef pair<int,int> PII; typedef complex<DB> CP; #define mmst(a,v) memset(a,v,sizeof(a)) #define mmcy(a,b) memcpy(a,b,sizeof(a)) #define fill(a,l,r,v) fill(a+l,a+r+1,v) #define re(i,a,b) for(i=(a);i<=(b);i++) #define red(i,a,b) for(i=(a);i>=(b);i--) #define ire(i,x) for(typedef(x.begin()) i=x.begin();i!=x.end();i++) #define fi first #define se second #define m_p(a,b) make_pair(a,b) #define p_b(a) push_back(a) #define SF scanf #define PF printf template<class T>inline T sqr(T x){return x*x;} template<class T>inline void upmin(T &t,T tmp){if(t>tmp)t=tmp;} template<class T>inline void upmax(T &t,T tmp){if(t<tmp)t=tmp;} const DB EPS=1e-9; inline int sgn(DB x){if(abs(x)<EPS)return 0;return(x>0)?1:-1;} const DB Pi=acos(-1.0); inline int gint() { int res=0;bool neg=0;char z; for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar()); if(z==EOF)return 0; if(z=='-'){neg=1;z=getchar();} for(;z!=EOF && isdigit(z);res=res*10+z-'0',z=getchar()); return (neg)?-res:res; } inline LL gll() { LL res=0;bool neg=0;char z; for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar()); if(z==EOF)return 0; if(z=='-'){neg=1;z=getchar();} for(;z!=EOF && isdigit(z);res=res*10+z-'0',z=getchar()); return (neg)?-res:res; } const int maxN=8; const LL Mod=1000000009LL; int N,M; int s[2*maxN+10],t[2*maxN+10]; int F[maxN+2][maxN+2][(1<<maxN)+10][(1<<maxN)+10]; int ans; #define wei(v,k) ((v>>(k-1))&1) #define bit(k) (1<<((k)-1)) #define two(k) (1<<(k)) int main() { freopen("str.in","r",stdin); freopen("str.out","w",stdout); int i,j,k; for(int Case=gint();Case;Case--) { N=gint();M=gint(); re(i,1,N+M-1)s[i]=getchar()-'A'+1;SF("\n"); re(i,1,N+M-1)t[i]=getchar()-'A'+1;SF("\n"); mmst(F,0); re(k,1,26)if(s[1]==k && t[1]==k) F[1][1][bit(1)][bit(1)]++; int s1,s2; re(i,1,N) { re(j,1,M-1) { re(s1,0,two(M)-1)re(s2,0,two(M)-1) { if(F[i][j][s1][s2]==0)continue; int a1=wei(s1,j),a2=wei(s1,j+1),b1=wei(s2,j),b2=wei(s2,j+1),len=i+j+1-1; re(k,1,26) { int news1,news2; if(s[len]==k && (a1 || a2)) news1=s1-a2*bit(j+1)+bit(j+1); else news1=s1-a2*bit(j+1); if(t[len]==k && (b1 || b2)) news2=s2-b2*bit(j+1)+bit(j+1); else news2=s2-b2*bit(j+1); F[i][j+1][news1][news2]=(F[i][j+1][news1][news2]+F[i][j][s1][s2])%Mod; } } } if(i==N)continue; re(s1,0,two(M)-1)re(s2,0,two(M)-1) { if(F[i][M][s1][s2]==0)continue; int a1=wei(s1,1),b1=wei(s2,1),len=i+1+1-1; re(k,1,26) { int news1,news2; if(s[len]==k && a1) news1=s1; else news1=s1-a1*bit(1); if(t[len]==k && b1) news2=s2; else news2=s2-b1*bit(1); F[i+1][1][news1][news2]=(F[i+1][1][news1][news2]+F[i][M][s1][s2])%Mod; } } } ans=0; re(s1,0,two(M)-1)re(s2,0,two(M)-1)if(wei(s1,M)==1 && wei(s2,M)==1)ans=(ans+F[N][M][s1][s2])%Mod; cout<<ans<<endl; }; return 0; }




