bzoj 1195

http://www.lydsy.com/JudgeOnline/problem.php?id=1195

状压DP。

首先去掉被包含的字符串。

对于字符串i和j，我们求出 当字符串j的左端点在字符串i的左端点的左边或与字符串i的左端点重合时，字符串i和字符串j可以重合的最长长度cost是多少。

就是求下面红色部分的最长长度cost：

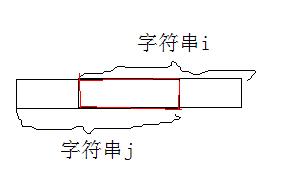
这个强行枚举就可以了，反正数据这么小。

注意，因为我们已经去掉了被包含的字符串，所以不会出现下面这种情况：

所以去掉了被包含的字符串是为了保证当左端点单调时，右端点也是单调的。

建一个图，我们在图中i连到j一条费用为cost的有向边。

然后就是求不重复经过点，可以走的最长路径。

这是哈密顿路径问题，为NP问题，但是这道题数据范围很小，可以用状压DP。

对于输出字典序最小字符串那里，我们在找决策的时候比较一下即可。

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<fstream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<utility>
#include<set>
#include<bitset>
#include<vector>
#include<functional>
#include<deque>
#include<cctype>
#include<climits>
#include<complex>
//#include<bits/stdc++.h>适用于CF,UOJ，但不适用于poj
 
using namespace std;

typedef long long LL;
typedef double DB;
typedef pair<int,int> PII;
typedef complex<DB> CP;

#define mmst(a,v) memset(a,v,sizeof(a))
#define mmcy(a,b) memcpy(a,b,sizeof(a))
#define fill(a,l,r,v) fill(a+l,a+r+1,v)
#define re(i,a,b)  for(i=(a);i<=(b);i++)
#define red(i,a,b) for(i=(a);i>=(b);i--)
#define ire(i,x) for(typedef(x.begin()) i=x.begin();i!=x.end();i++)
#define fi first
#define se second
#define m_p(a,b) make_pair(a,b)
#define SF scanf
#define PF printf


template<class T>inline T sqr(T x){return x*x;}
template<class T>inline void upmin(T &t,T tmp){if(t>tmp)t=tmp;}
template<class T>inline void upmax(T &t,T tmp){if(t<tmp)t=tmp;}

const DB EPS=1e-9;
inline int sgn(DB x){if(abs(x)<EPS)return 0;return(x>0)?1:-1;}
const DB Pi=acos(-1.0);

inline int gint()
  {
        int res=0;bool neg=0;char z;
        for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar());
        if(z==EOF)return 0;
        if(z=='-'){neg=1;z=getchar();}
        for(;z!=EOF && isdigit(z);res=res*10+z-'0',z=getchar());
        return (neg)?-res:res; 
    }
inline LL gll()
  {
      LL res=0;bool neg=0;char z;
        for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar());
        if(z==EOF)return 0;
        if(z=='-'){neg=1;z=getchar();}
        for(;z!=EOF && isdigit(z);res=res*10+z-'0',z=getchar());
        return (neg)?-res:res; 
    }

const int maxN=12;
const int maxlen=50;

int N;
char s[maxN+10][maxlen+10];

int tempN;
char temps[maxN+10][maxlen+10];
int f[maxN+10];

inline int smaller(char *s1,char *s2,int l1,int l2)
  {
      int i,len1=strlen(s1+1),len2=strlen(s2+1);
      re(i,1,min(len1-l1+1,len2-l2+1))if(s1[l1+i-1]!=s2[l2+i-1])return s1[l1+i-1]<s2[l2+i-1];
      return len1-l1+1<len2-l2+1;
  }

inline int same(char *s1,char *s2,int l1,int l2,int len)
  {
      int i;
      if(l1+len-1>strlen(s1+1))return 0;
      if(l2+len-1>strlen(s2+1))return 0;
      re(i,1,len)if(s1[l1+i-1]!=s2[l2+i-1])return 0;
      return 1;
  }

inline int check(char *s1,char *s2)
  {
      int i,l1=strlen(s1+1),l2=strlen(s2+1);
      re(i,1,l2-l1+1)if(same(s1,s2,1,i,l1))return 1;
      return 0;
  }

int now,first[maxN+10];
struct Tedge{int v,cost,next;}edge[maxN*maxN+100];
inline void addedge(int u,int v,int cost){now++;edge[now].v=v;edge[now].cost=cost;edge[now].next=first[u];first[u]=now;}

#define two(k) (1<<((k)-1))
#define wei(v,k) ((v>>(k-1))&1)

int F[maxN+10][(1<<maxN)+100],vis[maxN+10][(1<<maxN)+100];
int head,tail;PII que[maxN*(1<<maxN)+100000];

int cnt;char out[maxN*maxlen+1000];

int main()
  {
      /*freopen("substr.in","r",stdin);
      freopen("substr.out","w",stdout);*/
      int i,j;
      N=gint();
      re(i,1,N)SF("%s\n",s[i]+1);
      re(i,1,N)re(j,1,N)if(i!=j)if(check(s[i],s[j])){f[i]=1;break;}
      mmcy(temps,s);
        tempN=N;N=0;
      re(i,1,tempN)if(!f[i])mmcy(s[++N],temps[i]);
      if(N==0)N=1;
      
      now=-1;mmst(first,-1);
      re(i,1,N)re(j,1,N)if(i!=j)
        {
            int leni=strlen(s[i]+1),lenj=strlen(s[j]+1),res=lenj;
            while(res!=0 && !same(s[i],s[j],1,lenj-res+1,res))res--;
            addedge(i,j,res);
        }
      
      mmst(F,-1);mmst(vis,0);
      head=0;tail=-1;
      re(i,1,N)F[i][two(i)]=0,vis[i][two(i)]=1,que[++tail]=PII(i,two(i));
      while(head<=tail)
        {
            int u=que[head%(maxN*(1<<maxN)+100000)].fi,state=que[head%(maxN*(1<<maxN)+100000)].se,v,cost;head++;
            vis[u][state]=0;
            for(i=first[u],v=edge[i].v,cost=edge[i].cost;i!=-1;i=edge[i].next,v=edge[i].v,cost=edge[i].cost)
              if(!wei(state,v) && F[u][state]+cost>F[v][state+two(v)])
                {
                    F[v][state+two(v)]=F[u][state]+cost;
                    if(!vis[v][state+two(v)])
                      {
                          vis[v][state+two(v)]=1;
                          que[(++tail)%(maxN*(1<<maxN)+100000)]=PII(v,state+two(v));
                      }
                }
        }
      
      now=-1;mmst(first,-1);
      re(i,1,N)re(j,1,N)if(i!=j)
        {
            int leni=strlen(s[i]+1),lenj=strlen(s[j]+1),res=lenj;
            while(res!=0 && !same(s[i],s[j],1,lenj-res+1,res))res--;
            addedge(j,i,res);
        }
      
      int u=-1,state=two(N+1)-1;
      re(i,1,N)if(u==-1 || F[u][state]<F[i][state] || (F[u][state]==F[i][state] && smaller(s[i],s[u],1,1)))u=i;
      re(i,1,strlen(s[u]+1))out[++cnt]=s[u][i];
      for(int T=N-1;T;T--)
        {
            int p=-1,o,v,cost;
            for(i=first[u],v=edge[i].v,cost=edge[i].cost;i!=-1;i=edge[i].next,v=edge[i].v,cost=edge[i].cost)
              if(wei(state,v) && F[v][state-two(u)]+cost==F[u][state])
                if(p==-1 || smaller(s[v],s[p],cost+1,o))
                  p=v,o=cost+1;
            re(i,o,strlen(s[p]+1))out[++cnt]=s[p][i];
                state-=two(u);
            u=p;
        }
      re(i,1,cnt)putchar(out[i]);putchar('\n');
      return 0;
  }