最长回文子串问题（四种方法）

本文记录最长回文子串问题的四种解决方法，包括：

问题 

从给定的字符串 s 中找到最长的回文子串的长度。

例如 s = "babbad" 的最长回文子串是 "abba" ，长度是 4 。

leetcode 题目 - 最长回文子串

回文串的判断 

首先，回文串的判断方法是简单的：从两边向中间，不断比较头尾字符是否相同即可。

 

判断回文串 - C 语言实现 
// 判断给定字符串是否是回文串
bool IsPalindromicString(char *s) {
    int n = strlen(s);
    int left = 0;
    int right = n - 1;

    while (left < right) {
        if (s[left] == s[right]) {
            left++;
            right--;
        } else {
            return false;
        }
    }
    return true;
}

时间复杂度是 O(n)O(n) 。

中心扩展方法 

中心扩展方法的思路是非常自然的：

遍历每一个字符，向两边扩展找到以其为中心的最长回文子串， 所有找到的回文子串的最大长度即所求 。

 

不过，以当前字符为中心的回文串的长度可能是奇数，也可能是偶数，两种情况都需要考察：

  1. 奇数的情况：

     

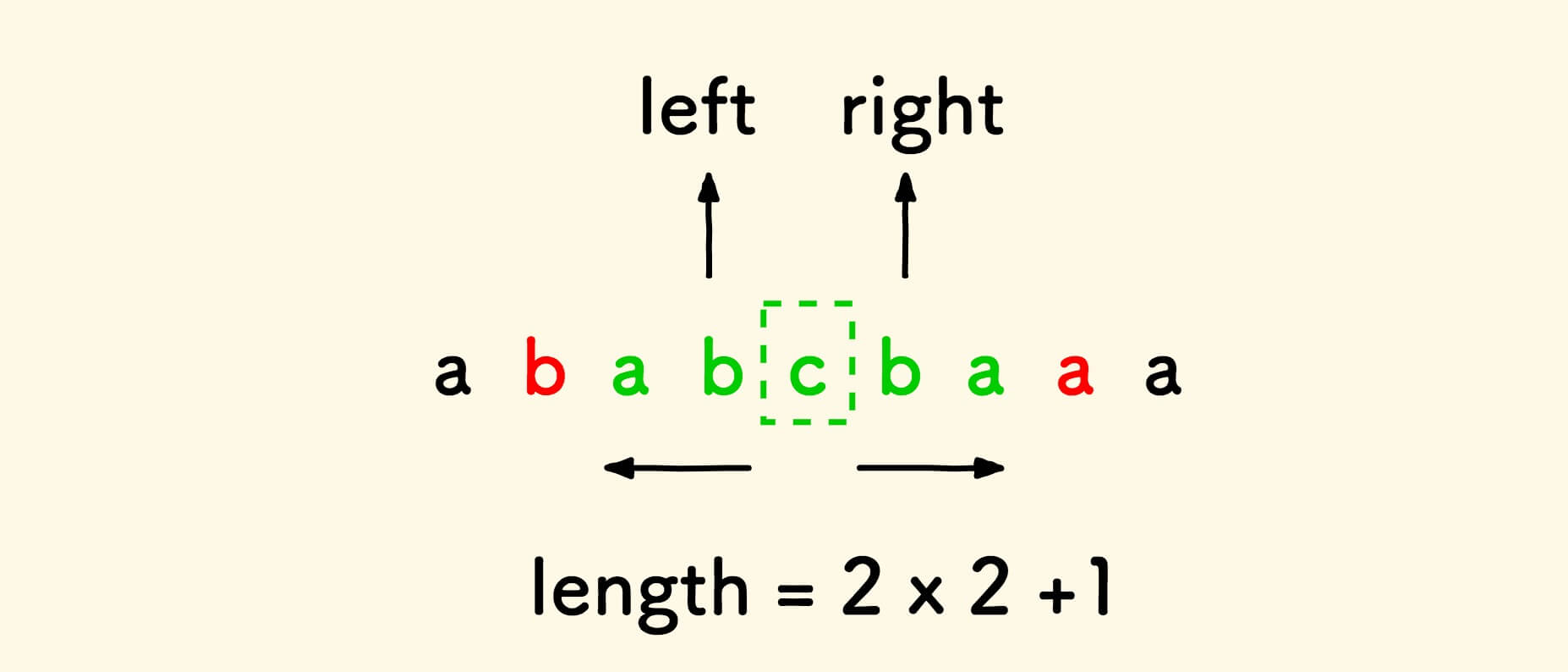
  2. 偶数的情况：

     

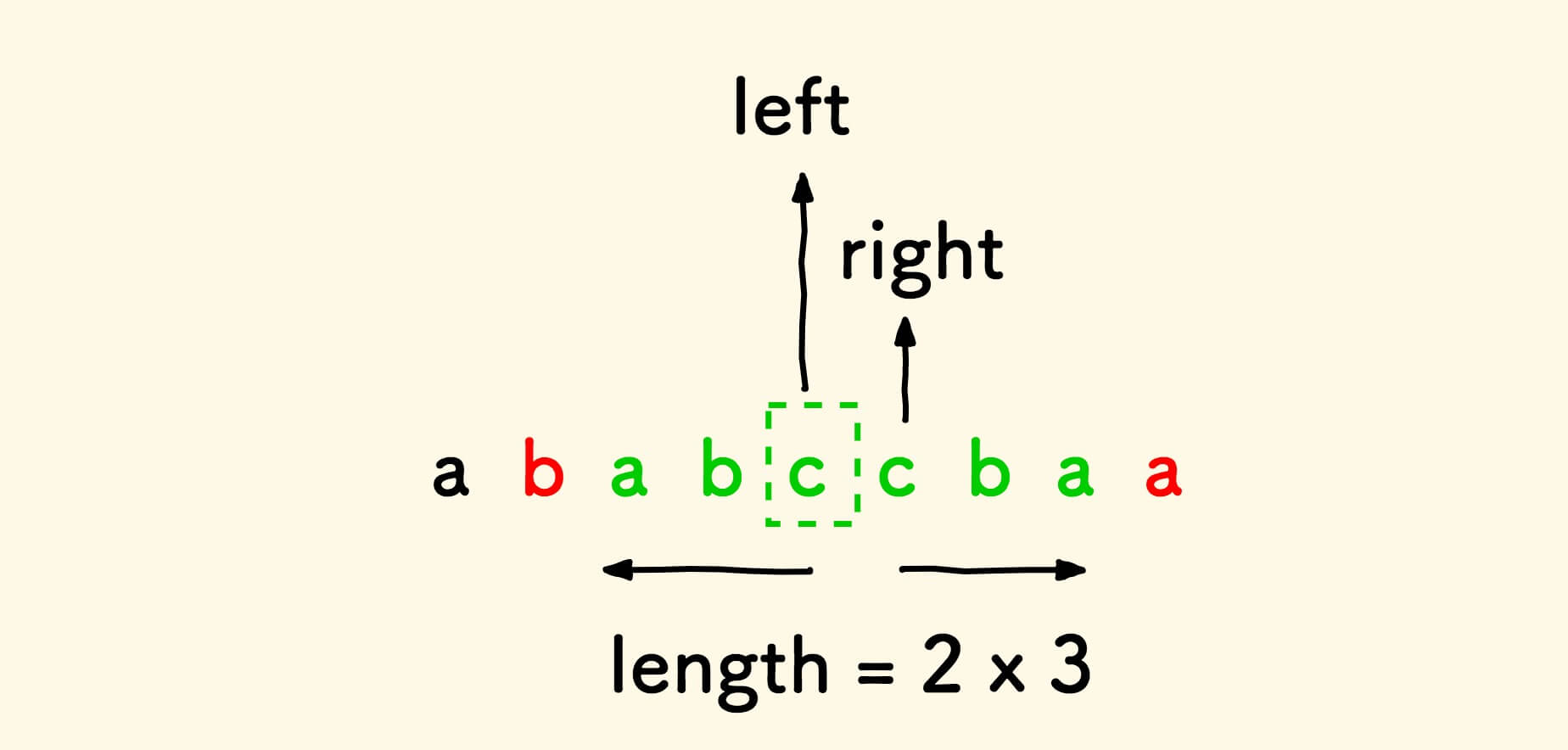
两种情况的扩展起始点和回文串的计算方式是不同的。

显然，这种方法的时间复杂度是 O(n2)O(n2) 。

最长回文子串 - 中心扩展法 - C 语言实现 
// 辅助函数：从长度为 n 的字符串 s 的给定位置左右扩展寻找回文串。
// 输入的 left 和 right 是扩展的左右起始位置。
// 返回回文子串的长度
int isPalindromicString(char* szString, int nLeft, int nRight)
{
    uint16_t nLen = strlen(szString);
    while (nLeft>0 && nRight<nLen) {
        if (szString[nLeft]==szString[nRight]) {
            nLeft--;
            nRight++;
        }
        else{
            break;
        }
    }
    return nRight-nLeft-1;
}

// 返回给定字符串 s 的最长回文子串的长度
int LongestPalindromicSubstring(char *szDestStr) {
    uint16_t nLen = strlen(szDestStr);
    int nMaxPalindramicLen = 0;
    for (int i=0; i<nLen; ++i) {
        int len1 = isPalindromicString(szDestStr, i-1, i+1);
        int len2 = isPalindromicString(szDestStr, i, i+1);
        
        nMaxPalindramicLen = max(nMaxPalindramicLen, len1);
        nMaxPalindramicLen = max(nMaxPalindramicLen, len2);
    }
    return nMaxPalindramicLen;
}

 

一维动态规划方法 

采用动态规划的方法，使用一个一维数组 dp 。

dp[j] 表示以位置 j 结束的最长的回文子串的起始位置 i 。

 

例如，在上图中，对于字符串 "aaabcbaba" 来说 dp[6] = 2 。

显然，对于非空字符串来说，有 dp[0] = 0 。

首先，需要证明一个结论：

递推过程中，当前项的回文串最多比上一项的回文串长一对字符 。

其原因可以做一般性验证：设 p(j) 是以位置 j 结尾的最长回文子串。

 

把 p(j) 的左右字符剔除，形成的子串 p' 显然也是一个回文串。

 

因为 p(j-1) 是以位置 j-1 结尾的最长回文串，所以回文串 p' 不可比 p(j-1) 长。

进而说明了 p(j) 至多比 p(j-1) 长一对字符。

现在，假设已知 dp[j-1] ，将考虑如何递推 dp[j]，分两种情况：

  • 当前位置的字符和上一次回文串的左邻字符相同，回文串得到扩展。

     

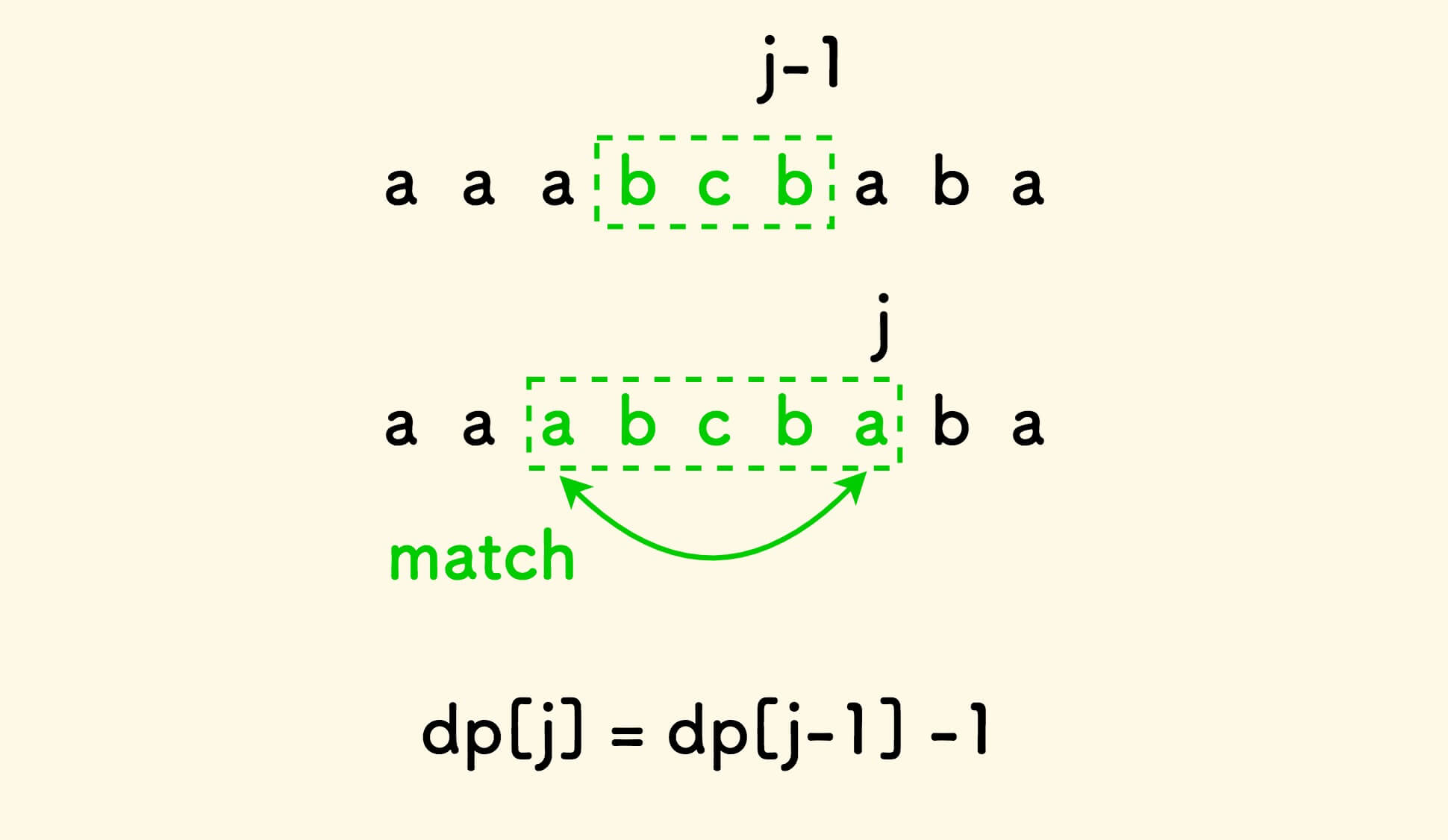
    易知，dp[j] = dp[j-1] - 1 。

    此外，由 前面的结论 可知，不会形成比它更长的回文串。

  • 否则，回文串未得到扩展，但仍可能形成回文串，比如：

     

    此时只能从左向右探测以位置 j 结尾的回文串。

    根据 前面的结论 ，可以从上一次回文串的起始位置开始探测。

    探测的方法是，起两个变量 left 和 right 对向比对字符：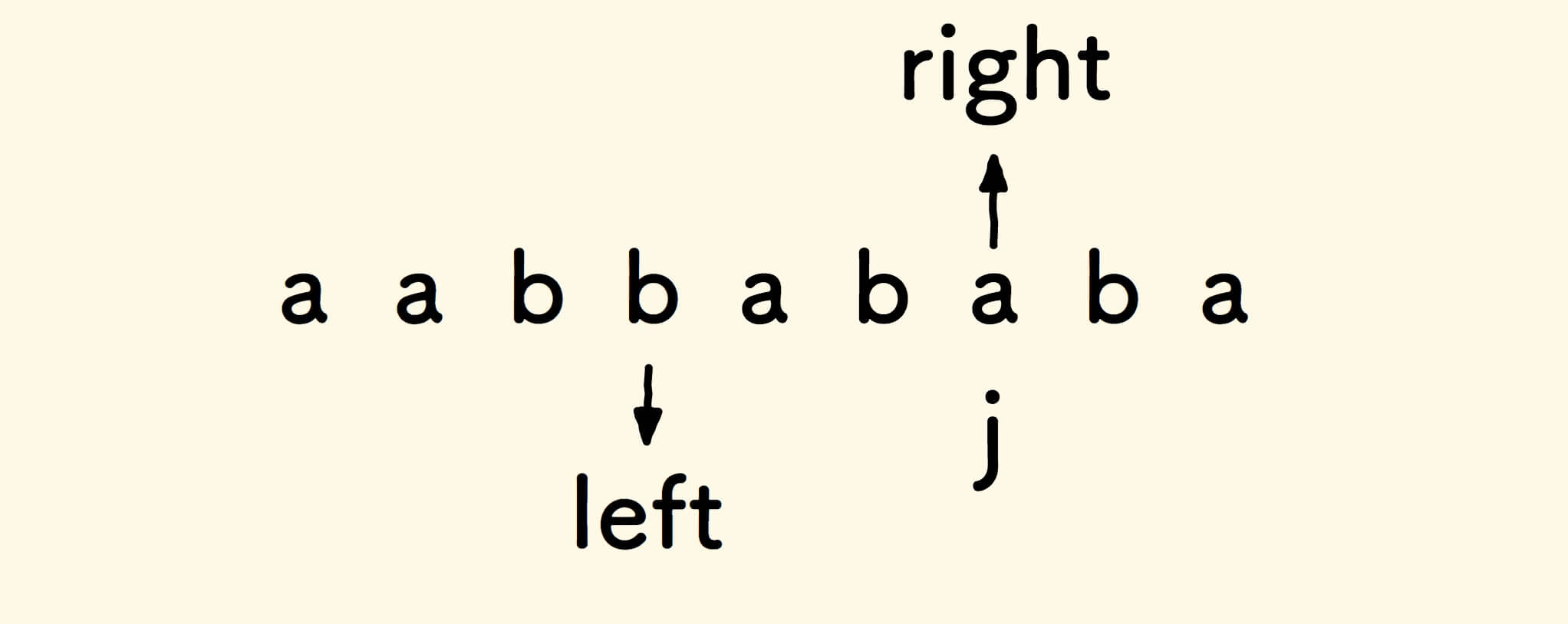

     

    遇到不匹配的字符，把 right 拉回右边，因为要找的是以位置 j 结尾的回文串。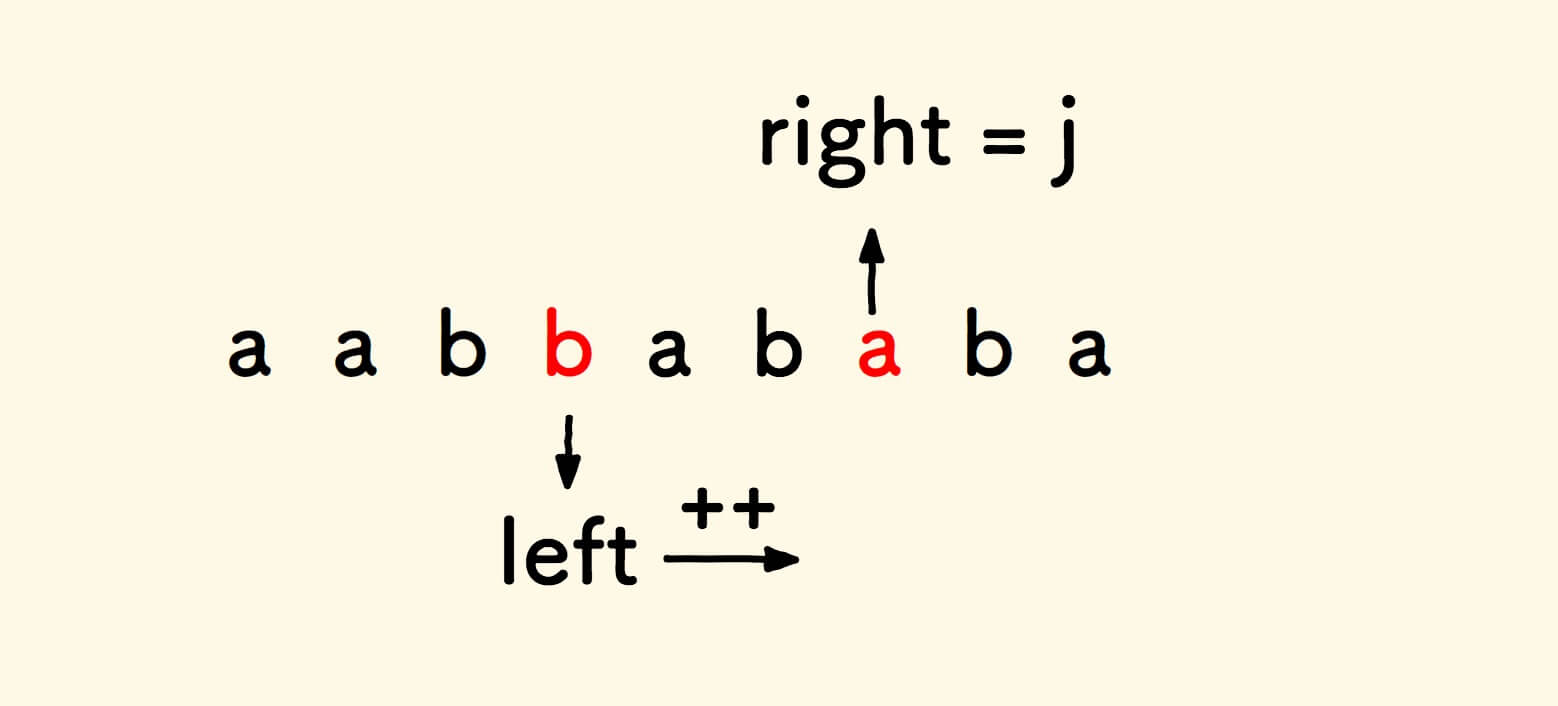

     

    遇到匹配的两个字符，则左右继续靠拢：

     

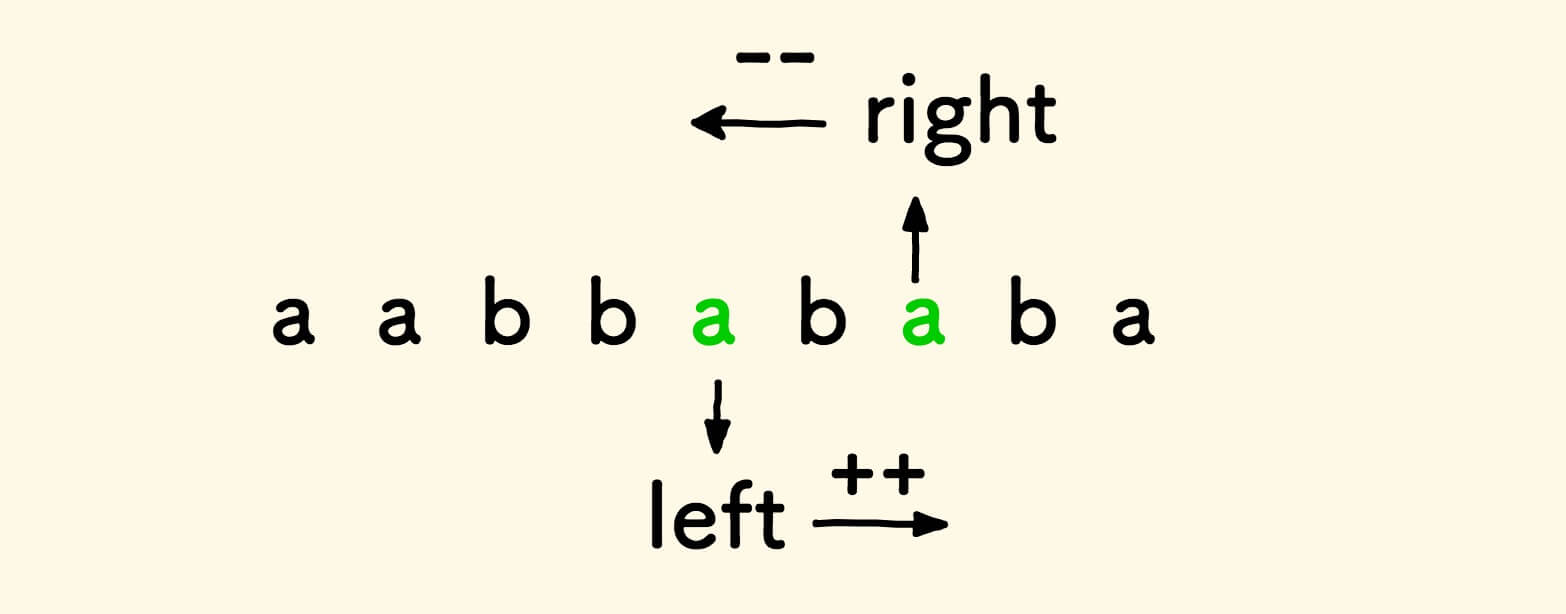
    直到左右变量相遇，就找到了一个回文串。

    在遭遇左右不匹配的时候，除了重置 right 之外，可以用一个变量记录当时 left 的位置， 这样在回文寻找完毕时，它就是回文串的起始位置，也就是 dp[j] 。

至此，递推关系分析完成。

最后，易找出最长回文串和它的长度，不再详细讨论。

相比前两个方法，此方法理解稍复杂，是自己想到的一种新的方法。

最长回文子串 - 一维动态规划方法 - C 语言实现
 

容易分析出来，这个算法的时间复杂度是 O(n2)O(n2) 。

二维动态规划方法 

相比 一维动态规划方法 而言， 二维数组上的动态规划方法的思路更直白。

回文串两边加上两个相同字符，会形成一个新的回文串 。

 

方法是，建立二维数组 dp ，找出所有的回文子串。

dp[i][j] 记录子串 i..j 是否为回文串 。

 

首先，单个字符就形成一个回文串，所以，所有 dp[i][i] = true 。

 

然后，容易得到递推关系：

如果字符 s[i] 和 s[j] 相等，并且子串 i+1..j-1 是回文串的话，子串 i..j 也是回文串。

也就是，如果 s[i] == s[j] 且 dp[i+1][j-1] = true 时，dp[i][j] = true 。

 

这是本方法中主要的递推关系。

不过仍要注意边界情况，即 子串 i+1..j-1 的有效性 ，当 i+1 <= j-1 时，它才有效。

反之，如果不满足，此时 j <= i+1 ，也就是子串 i..j 最多有两个字符， 如果两个字符 s[i] 和 s[j] 相等，那么是回文串。

至此，递推关系已经分析完。

最后，考虑到 主要的递推关系 是由已知子串 i+1..j-1 的情况， 递推到 i..j 的情况， 因此，迭代过程需要反序迭代变量 i ，正序迭代 j 。

此外，可以通过一个表格，来理解整个 dp 数组的规划过程。

 

上面的表格填表过程：

  1. 初始化所有方格写 false 。
  2. 填写对角线写 true 。
  3. 自对角线右下角开始，自下而上、自左而右，按箭头方向根据递推关系填表。

最后，找到所有回文子串后，即可找到最长回文子串和其长度。

最长回文子串 - 二维动态规划法 - C 语言实现
 

此方法的时间复杂度是 O(n2)O(n2) 。

Manacher 方法 

Manacher 算法 是一种线性时间内求解最长回文子串的算法，俗称「马拉车算法」。

Manacher 算法本身是面比较窄的算法，但背后其实也是基于动态规划思想的。

本部分内容较长、算法较复杂，需要精心阅读 。

算法分为两个过程：

  1. 预处理过程：通过插入分隔符的办法，把潜在的回文子串统一转为奇数长度。
  2. 算法主过程：构造回文半径数组，利用回文的对称性，递推回文半径。
预处理过程

预处理过程比较简单。

在原始字符串每个字符中间和整个字符串两边插入分隔符：

 

如果，原始字符串的长度是 nn ，那么预处理后的长度为 2n+12n+1 。

预处理后，任意一个回文串都是奇数长度。

容易给出预处理部分的代码实现，其复杂度是 O(n)O(n) 。

最长回文子串 - Manacher 算法 - 预处理 - C 语言实现
 
回文半径的概念

现在定义一个概念：

回文半径是回文串的中心字符到左边界的距离。

严格来说，是中心字符和左边界字符下标的差值。

简单来说，是 中心字符左边的字符个数 。

下图中的例子，绿色的回文串的半径是 p=2 。

 

可以发现，预处理后，回文半径就是原字符串中回文串的长度：

 

于是，接下来只需要考虑预处理后的字符串即可。

现在，建立一个回文半径的数组， p[i] 表示以位置 i 为中心的最长回文串的半径 。

 

找到数组 p 的最大值，就是原字符串的最长回文串的长度。

算法主过程

算法的主过程则是求解预处理后字符串的半径数组 p ，采用动态规划的方式。

首先，字符串第一位是分隔符，因此首位 p[0] = 0 。

下面考虑递推关系。

在求解半径数组 p 的过程中， 维护 向右延伸最远的回文串 的信息 。

假设我们处于求解 p[i] 的过程中， 下图中绿色的字符串就是要维护的 向右延伸最远的回文串 ， 它的右边界是已知的回文串中最大的。

 

对于这种字符串，不妨叫做 最右延伸回文串 ，维护它的信息：

  • 它的中心字符的位置 c
  • 它的右边界位置 r

 

在求解 p[i] 的迭代过程中，一旦遇到右边界比 r 还要大的回文串，就更新 r 和 c 的值。

现在尝试寻找以 i 为中心的最长回文串 q ，它的长度是未知的，有如下几种可能：

 

下面对以上的情况逐个分析：

  1. 当 i < r 且 q 被最右延伸回文串完全包住。

    找出 i 关于中心 c 的对称位置 j ，两边是完全镜像的，半径相等 p[i] = p[j] 。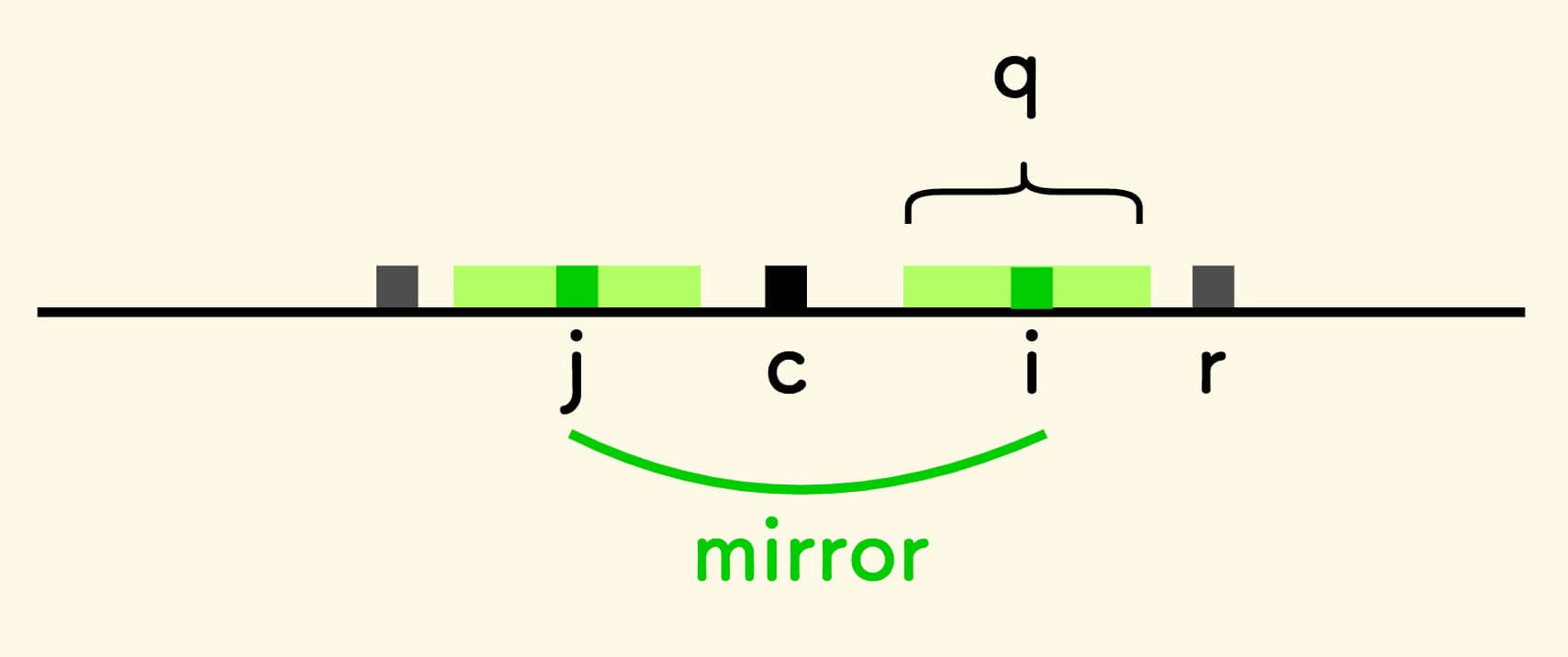

     

  2. 当 i < r ，但是同时 q 没有被完全包住。

    此时容易知道回文串 q 的半径不小于 r-i 。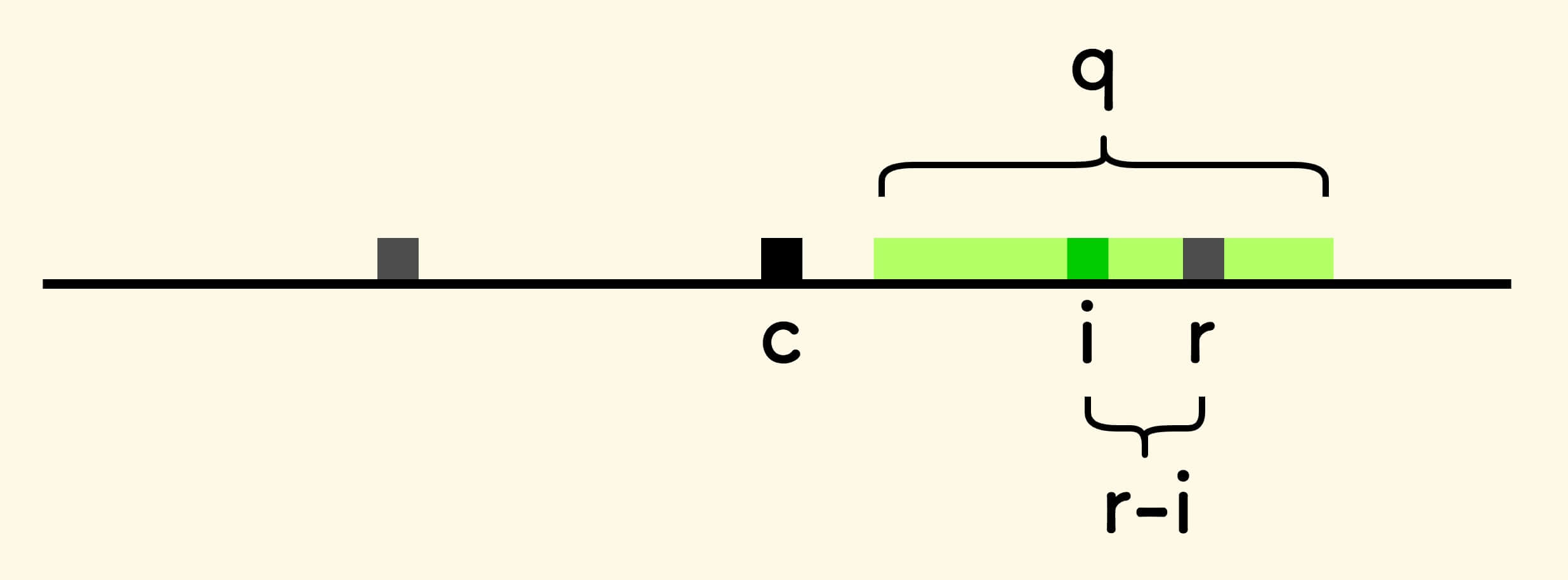

     

    综合第一种情况，可知， 当 i < r 时，p[i] 至少为 min(p[j], r-i) 。

    不过，右边跨过 r 的部分仍然是未知的，需要采用中心扩展方法求出。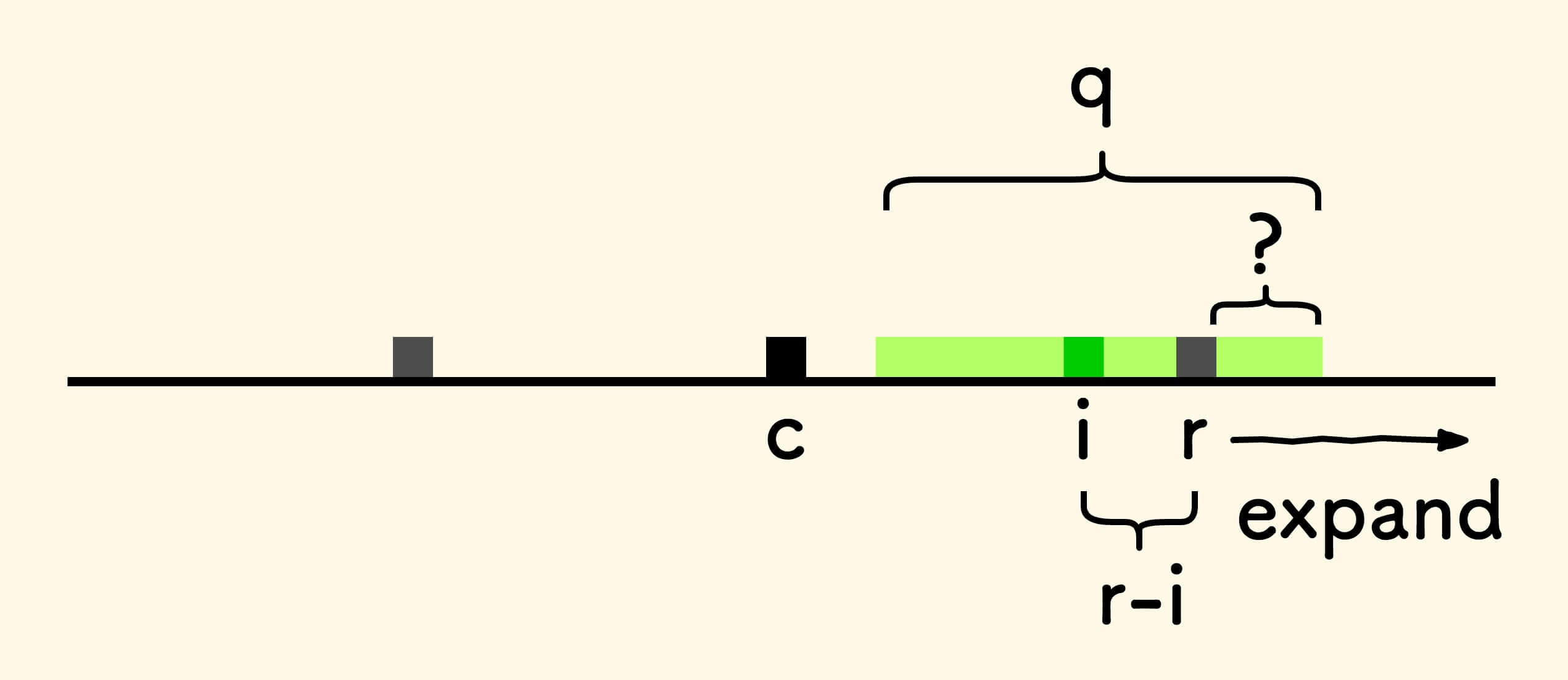

     

    已经知道，此时 p[i] 至少是 r-i ，因此只需要从 r+1 处开始扩展就行。

  3. 当 i >= r ，此时，只能从位置 i 处向两边中心扩展探测回文串。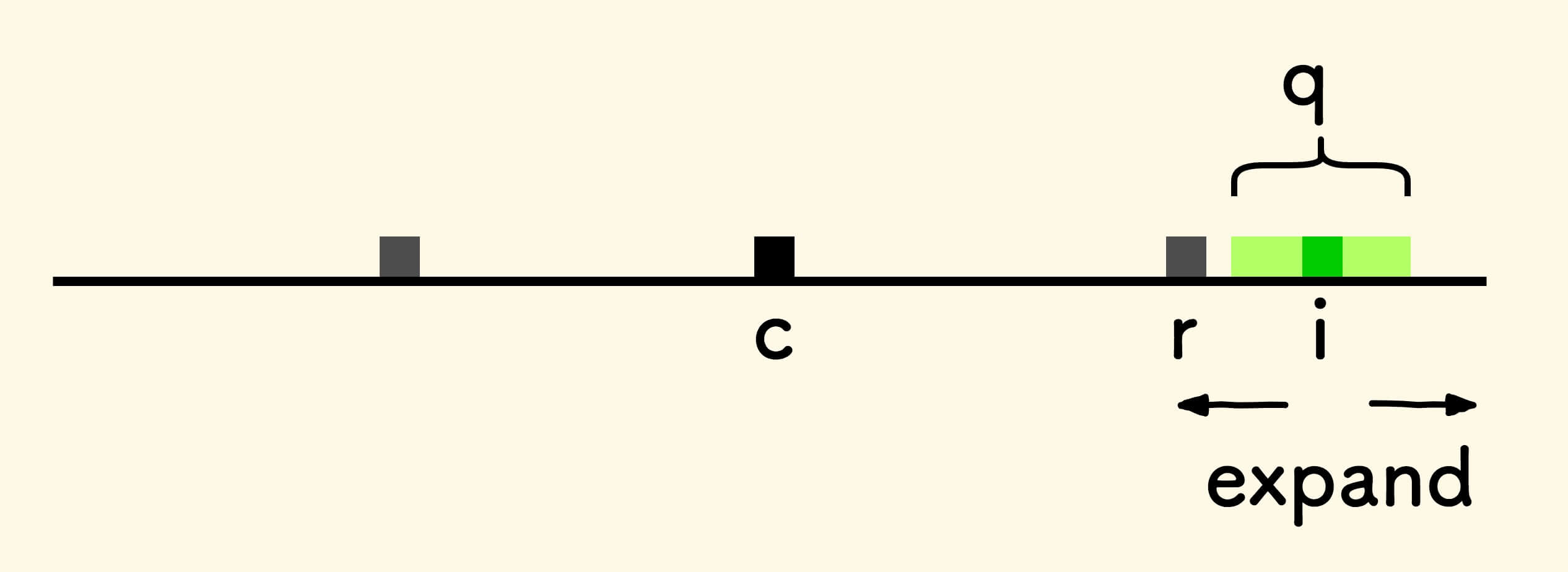

     

    具体来说，先初始化半径 p[i] = 0 ，然后不断尝试增加半径，判断左右字符是否相等。

    此时的中心扩展起点是 i+1 。

综合上面三种情况：

  1. 如果 i < r ，那么 p[i] 至少为 min(p[j], r-i) 。

    不妨让 p[i] 先取这个值，即先吸收已知信息。

  2. 然后向右中心扩展，探测回文串的边界。

    无论 i 和 r 的大小关系如何，左右扩展的起点可以统一表示 ，都可以表达为：

    • left = i - p[i] - 1
    • right = i + p[i] + 1

最终的递推关系，虽然分为三种情况，但是可以总结为：

先吸收已知的镜像半径长度，然后再中心扩展探测剩余长度 。

利用此递推关系，求解半径数组 p ，找出其中半径最大值，就是原字符串的最长回文串长度。

最长回文串 - Manacher 方法 - 算法主过程- C 语言实现
 
算法复杂度

最后，分析 Manacher 算法的时间复杂度。

易知，预处理过程时间复杂度是 O(n)O(n) 。

为方便分析算法主流程的时间复杂度，把其代码精简为伪代码如下：

Manacher 算法主流程 - 伪代码
 

算法主过程虽然有两层循环，但是内层循环只有在 后两种情况 发生时进入， 也就是只有当以 i 为中心的回文串 q 跨越最右边界 r 的时候才进入，这种情况下最右边界会增大。 导致后面的迭代过程中，第一种情况 就更容易发生。

内层循环的 right 起点是：

这两种情况下，内层循环起点至少 > r 。

内层循环结束后，都会更新 r 变大到新的右边界 right。

就是说， 本次内层循环的终点和下一次内层循环的起点无缝衔接 。

所以内层循环总的步数是线性的 n 次。

两层循环加起来的总步数就是 2n 次，时间复杂度即 O(n)O(n) 。

可以说，Manacher 算法最大化地利用了已知最右回文串的信息，才达到了线性时间复杂度。

结语 

本文解决最长回文子串问题的四种方法中， 最容易理解的思路是中心扩展法。 时间表现最好的是 Manacher 方法。

我个人比较喜欢的则是两个动态规划方法， 毕竟中心扩展法和 Manacher算法 是针对回文串问题的具体算法，动态规划的思想则更具一般性。

（完）

补充说明:

原来本文还介绍了一种错误的方法：

错误方法 - 最长公共子串方法

 

 

 

此方法由 @ph 在评论中指出反例：”abc12cba” .

相关阅读：

posted @ 2022-06-01 14:40  麦峰强  阅读(673)  评论(0)  编辑  收藏  举报