欧拉函数知识点

欧拉函数：

1.对正整数n，欧拉函数是小于n且和n互质的正整数(包括1)的个数。

例如Euler(8)=4，因为1,3,5,7均和8互质

2.φ(n) = n*(1-1/p1)*(1-1/p2)*......(1-1/pn)  

其中(p1.....pn)为N的素因子

3.欧拉函数的性质

① N是不为0的整数。φ(1)=1（唯一和1互质的数就是1本身）

② 除了N=2,φ(N)都是偶数.

③ 小于N且与N互质的所有数的和是φ(n)*n/2。

④ 欧拉函数是积性函数——若m,n互质，φ(m*n)=φ(m)*φ(n)。

⑤ 当N为奇数时，φ(2*N)=φ(N)

⑥ 若N是质数p的k次幂，φ(N)=p^k-p^(k-1)=(p-1)p^(k-1)，

因为除了p的倍数外，其他数都跟N互质。

⑦ 当N是质数时，φ(N) = N-1

8.

 

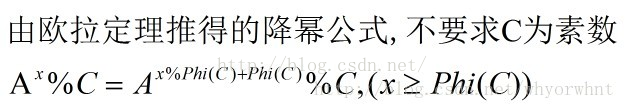
欧拉函数求法：

1.直接根据公式求

 1 ll Euler(ll n)
 2 {
 3     ll tmp=n,ans=n;
 4     for(ll i=2;i*i<=tmp;++i)
 5      if(tmp%i==0)
 6      {
 7          ans=ans/i*(i-1);
 8          while(tmp%i==0) tmp/=i;
 9      }
10     if(tmp>1) ans=ans/tmp*(tmp-1);
11     //最后只剩下小于4的素数或者n本身就是素数
12     return ans;
13 }

2.然当n比较大的时候用打表访问比较快，下面是筛选法打欧拉函数表 

 1 void init()
 2 {
 3     for(int i = 1 ; i <= MAXN ; i++)
 4         a[i] = i;
 5     a[1] = 0;
 6     for(int i = 1 ; i <= MAXN ; i++)
 7     {
 8         if(a[i] == i)
 9         {
10             for(int j = i ; j <= MAXN ; j += i)
11                 a[j] = a[j] / i * (i - 1);
12         }
13     }
14 }

 例题：

Relatives
Time Limit: 1000MS        Memory Limit: 65536K
Description
Given n, a positive integer, how many positive integers less than n are relatively prime to n? Two integers a and b are relatively prime if there are no integers x > 1, y > 0, z > 0 such that a = xy and b = xz.
Input
There are several test cases. For each test case, standard input contains a line with n <= 1,000,000,000. A line containing 0 follows the last case.
Output
For each test case there should be single line of output answering the question posed above.
Sample Input
7
12
0
Sample Output
6
4
Source
Waterloo local 2002.07.01

裸的欧拉函数。

 1 #include<algorithm>
 2 #include<iostream>
 3 #include<cstring>
 4 #include<string>
 5 #include<cstdio>
 6 #include<cmath>
 7 #define ll long long
 8 using namespace std;
 9 ll n;
10 ll Euler(ll n)
11 {
12     ll tmp=n,ans=n;
13     for(ll i=2;i*i<=n;++i)
14     if(tmp%i==0)
15     {
16         ans=ans*(i-1)/i;
17         while(tmp%i==0) tmp/=i;
18     }
19     if(tmp>1) ans=ans*(tmp-1)/tmp;
20     return ans;
21 }
22 int main()
23 {
24     while(scanf("%lld",&n)!=EOF)
25     {
26         if(n==0) break;
27         printf("%lld\n",Euler(n));
28     }
29     fclose(stdin);fclose(stdout);
30     return 0;
31 }