卡特兰数
卡特兰数又称卡塔兰数,卡特兰数是组合数学中一个常出现在各种计数
问题中的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)
的名字来命名。
(重点)前几项为 :
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,
16796, 58786, 208012, 742900, 2674440, 9694845, 35357670,
129644790, 477638700, 1767263190, 6564120420, 24466267020,
91482563640, 343059613650, 1289904147324, 4861946401452, ...
(重点)相关递推式:
h[n]=C(2n,n)-C(2n,n-1)
h[n]=h[n-1]*(4*n-2)/(n+1)
(重中之重)应用:(没有原理,只有结论,有时间记得去看看证明)
卡特兰数的应用:
1. 由n个 +1 和n个 -1 构成 2n 项的数列 a1,a2,a3,a4.......
其部分和满足 a1+a2+a3+ak>=0 0<=k<=2n
这样的数列个数为h[n]
2.我们可以将应用1变换形式:
将 -1 看成右括号,+1 看成左括号,就变成了左括号和右括号各有n个时,合法括号表达式的个数。
比如2个左括号和2个右括号组成的合法表达式有h[2] = 2种,是()()和(())。
3.再次转换形式: 对于 n+1 个数连乘,乘法顺序有h[n]种
比如三个数连乘 a*b*c ,n=2 ,相当于在式子上加括号,
有2种乘法顺序,分别是 (a*b)*c 和 a*(b*c)。
四个数连乘a*b*c*d,n=3,有5种乘法顺序,
分别是a(b(cd)),(ab)(cd),((ab)c)d,(a(bc))d和a((bc)d)
4.n个节点构造二叉树的所有可能形态数为h[n].
5. n个非叶节点的满二叉树的形态数为h[n]
(如果一棵二叉树的结点要么是叶子结点,要么它有两个孩子结点,这样的树就是满二叉树)
(对称后得到的二叉树除非自己本身对称,否则算是不同)
例子:n=3 h[3]=5

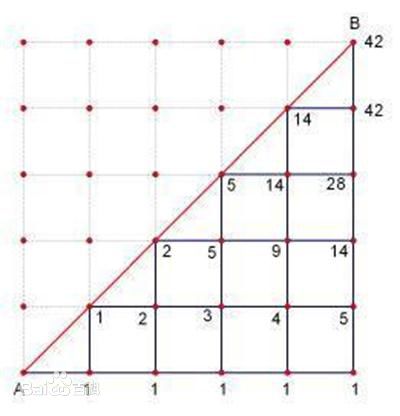
6.对于一个n*n的正方形网格,每次只能向右或者向上移动一格,
那么从左下角到右上角所有在副对角线(下图中虚线)右下方的路径总数为h[n]
例子: n=4 h[4]=14
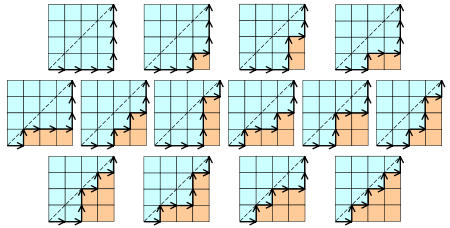
可以将一条水平边记为+1,垂直边记为-1,那么就组成了一个n个+1和n个-1的序列,
并且保证前k步中水平边数不小于垂直边数,换句话说前k个元素的和非负。
7.对凸n+2边形进行不同的三角形分割(只连接顶点对形成n个三角形)数为h[n]
例子: n=4 h[4]=14
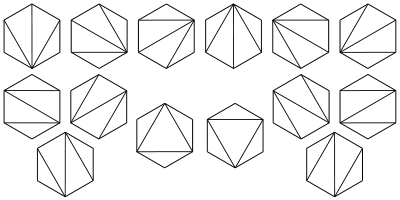
8. 平面上连接可以形成凸包的2n个点分成2个一组连成n条线段,两两线段之间不相交的情况总数是h[n].
这其实和上面的第7类是一样的
类似的有:(1)在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数
(2)一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
9.n个数入栈后的出栈的排列总数是h[n]。
例如1,2,3入栈的出栈排序有123,132,213,231和321五种
10. 对于集合{1,2,3,.....2*n},将集合元素两两分为n个子集,若任意两个子集都不交叉,那么我们称此划分为一个不交叉划分。
此时不交叉的划分数就是h[n]。
考虑将每个子集中较小的数用左括号代替,较大的用右括号代替,那么带入原来的1至2n的序列中就形成了合法括号问题。
例如集合{1,2,3,4,5,6}的不交叉划分有五个:
{{1,2}, {3,4}, {5,6}}, {{1,2},{3,6},{4,5}}, {{1,4},{2,3},{5,6}},{{1,6},{2,3},{4,5}} 和 {{1,6},{2,5},{3,4}}。
11.n层的阶梯切割为n个矩形的切法数也是h[n].
例子: n=4 h[4]=14

12. 在一个2*n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和上边的所有数值都小的情况数也是h[n].
13.买票找零
有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,
问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?
(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)方案数为h[n]
参考博客:http://blog.csdn.net/zhangmh93425/article/details/44677891
例题:
洛谷 1044 栈
洛谷 1722 矩阵 II
洛谷 1976 鸡蛋饼
洛谷 2532 [AHOI2012]树屋阶梯
洛谷 3200 [HNOI2009]有趣的数列


