最大权闭合子图

定义：

所谓闭合子图就是给定一个有向图，从中选择一些点组成一个点集V。对于V中任意一个点，其后续节点都仍然在V中。比如

 

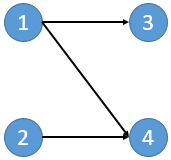
在这个图中有8个闭合子图：∅,{3},{4},{2,4},{3,4},{1,3,4},{2,3,4},{1,2,3,4}

最大权闭合子图就是所有的闭合子图中权值和最大的一个。

如下图：

 

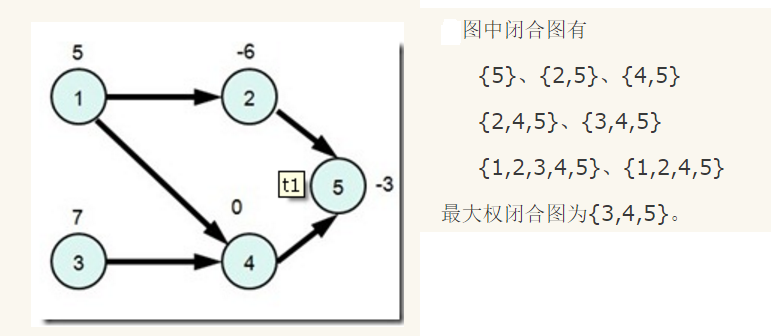
对于最大权闭合子图问题，模型转换如下：

增设一个超级源点S和一个超级汇点T，

（1->n）的点中，当点权为正时，从源点向该点连一条权值为点权大小的边，

当点权为负时，从该点连一条权值大小为它的绝对值的边连向汇点。

这种问题一般都是对于（u，v），如果选择u必须选择v，对（u，v）连一条容量为oo的边。

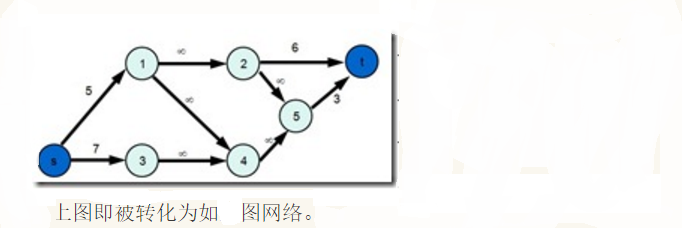
建完模型之后，答案=所有正的点权值之和-最小割

证明：略