向量积&&凸包算法

参考：Thanks

百度百科

http://blog.csdn.net/keng_s/article/details/52131034

https://www.cnblogs.com/aiguona/p/7232243.html

一定要有耐心，仔细的看。(#^.^#)

预备：

向量积

概念：

向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。

 

计算：a,b,c均为向量

向量的叉乘，即求同时垂直两个向量的向量，即c垂直于a，同时c垂直于b（a与c的夹角为90°，b与c的夹角为90°）

c =  a×b = （a.y*b.z-b.y*a.z , b.x*a.z-a.x*b.z  , a.x*b.y-b.x*a.y）

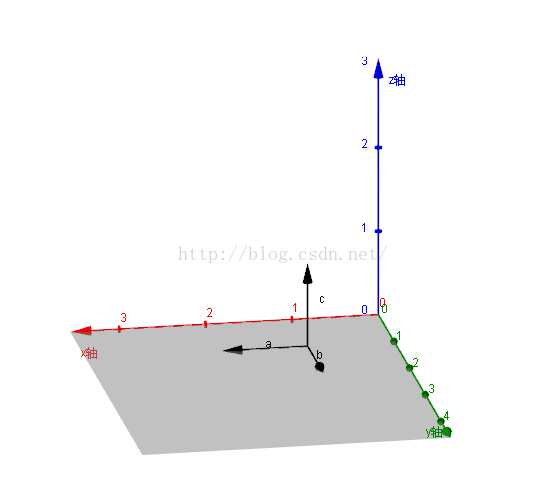
以上图为例a(1,0,0),b(0,1,0),c=a×b = (0,0,1) 

 相关：

向量积|c|=|a×b|=|a| |b|sin<a,b>

即c的长度在数值上等于以a，b，夹角为θ组成的平行四边形的面积。

如果a,b的叉积|c|的数值>0 说明 b在a的逆时针方向

                       |c|的数值=0 说明 b和a在一条直线上

                       |c|的数值<0 说明 b在a的顺时针方向

 ===========================================================分割线

凸包

概念：

1.在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称  为X的凸包。X的凸包可以用X内所有点(X1，...Xn)的凸组合来构造.
2. 在二维欧几里得空间中，凸包可想象为一条刚好包著所有点的橡皮圈。
3. 用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有的点。

 

定义：

1.点集Q的凸包（convex hull）是指一个最小凸多边形，满足Q中的点或者在多边形边上或者在其内。下图中由红色线段表示的多边形就是点集Q={p0,p1,...p12}的凸包。

 

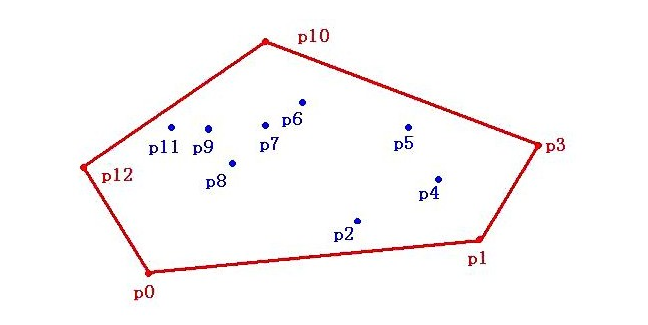
2.一组平面上的点，求一个包含所有点的最小的凸多边形，这就是凸包问题了。这可以形象地想成这样：在地上放置一些不可移动的木桩，用一根绳子把他们尽量紧地圈起来，并且为凸边形，这就是凸包了。

 

 

常用求法：

Graham扫描法

过程：

1.在所有点中选取y坐标最小的一点H，当作基点。如果存在多个点的y坐标都为最小值，则选取x坐标最小的一点。。坐标相同的点应排除。

然后按照其它各点p和基点构成的向量<H,p>；与x轴的夹角进行排序，夹角由大至小进行顺时针扫描，反之则进行逆时针扫描。实现中无需求得夹角，只需根据余弦定理求出向量夹角的余弦值即可。

以下图为例，基点为H，根据夹角由小至大排序后依次为H，K，C，D，L，F，G，E，I，B，A，J。下面进行逆时针扫描。

 

 

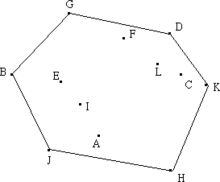
 2.线段<H,K>；一定在凸包上，接着加入C。假设线段<K,C>；也在凸包上，因为就H，K，C三点而言，它们的凸包就是由此三点所组成。但是接下来加入D时会发现，线段<K,D>；才会在凸包上，所以将线段<K,C>；排除，C点不可能是凸包。

3. 即当加入一点时，必须考虑到前面的线段是否在凸包上。

基点开始，凸包上每条相临的线段的旋转方向应该一致，并与扫描的方向相反。

如果发现新加的点使得新线段与上线段的旋转方向发生变化，则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断。

设新加入的点为P[n+1],上一点为P[n],再上一点为P[n-1]。顺时针扫描时，如果向量

(P[n-1],P[n])与(P[n],P[n+1])的叉积为正（逆时针扫描判断是否为负），则将上一点删除。删除过程需要回溯，将之前所有叉积符号相反的点都删除，然后将新点加入凸包。

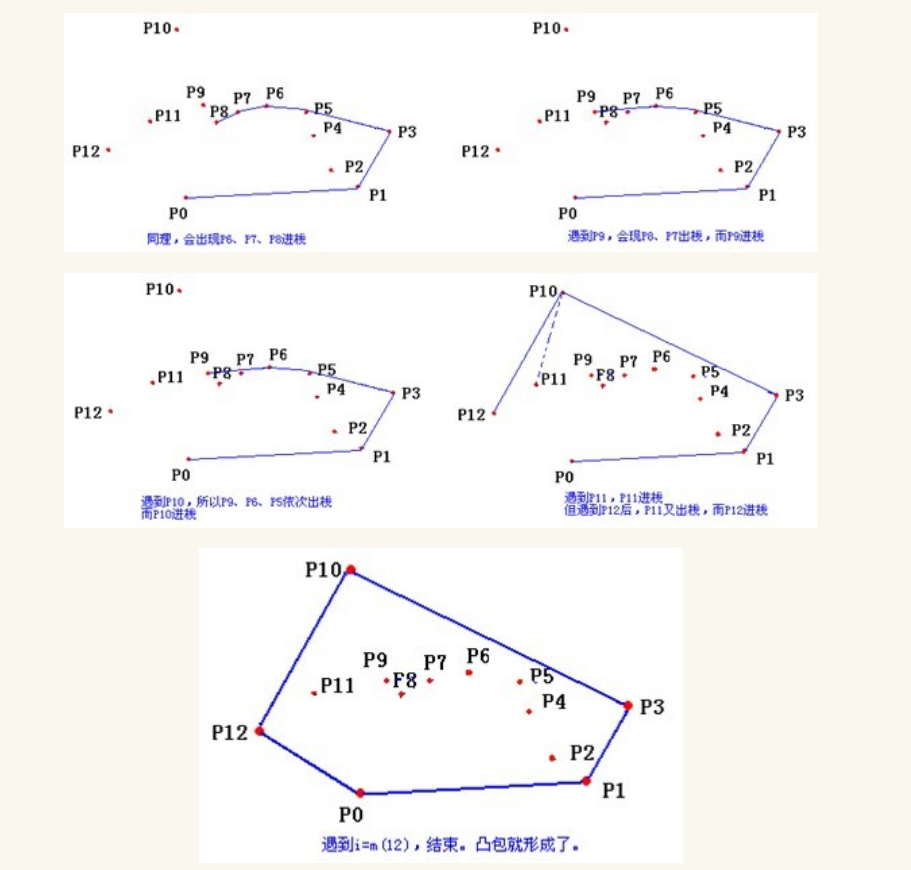
在上图中，加入K点时，由于线段<H,C>要旋转到<H,K>的角度，为顺时针旋转，所以C点不在凸包上，应该删除，保留K点。接着加入D点，由于线段<K,D>要旋转到<H,K>的角度，为逆时针旋转，故D点保留。按照上述步骤进行扫描，直到点集中所有的点都遍历完成，即得到凸包.

 

复杂度：

这个算法可以直接在原数据上进行运算，因此空间复杂度为O⑴。但如果将凸包的结果存储到另一数组中，则可能在代码级别进行优化。由于在扫描凸包前要进行排序，因此时间复杂度至少为快速排序的O(nlgn)。后面的扫描过程复杂度为O(n)，因此整个算法的复杂度为O(nlgn)。

模拟图片：

 

 模板：

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define PI 3.1415926535
#define DB double
#define eps 1e-8
using namespace std;
const int N=12000;
int T,n,L;
struct node{
    DB x,y;
}d[N],s[N];//d[]存入的所有的点  s[]凸包中所有的点
bool cmp1(node a,node b)
{
    if(a.y!=b.y) return a.y<b.y;
    else return a.x<b.x;
}
DB Cross(node a1,node a2,node b1,node b2)
{
    return (a2.x-a1.x)*(b2.y-b1.y)-(b2.x-b1.x)*(a2.y-a1.y);
}
DB dis(node a,node b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y));
}
bool cmp2(node a,node b)//极角排序,原理见紫色部分 
{
    DB m=Cross(d[1],a,d[1],b);
    if(m>0) return 1;
    else if(m==0) return dis(d[0],a)<dis(d[0],b);
    return 0;
}
int top;
DB ans;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i)scanf("%lf%lf",&d[i].x,&d[i].y);
    sort(d+1,d+n+1,cmp1);
    s[++top]=d[1];
    sort(d+2,d+n+1,cmp2);
    s[++top]=d[2];
    for(int i=3;i<=n;++i)
    {
        while(top>=2 && Cross(s[top-1],s[top],s[top],d[i])<=0) top--;
        //控制<0或<=0可以控制重点，共线的，具体视题目而定 
        s[++top]=d[i];
    }
    for(int i=1;i<top;++i)ans+=dis(s[i],s[i+1]);
    ans+=dis(s[1],s[top]);
    printf("%.2lf\n",ans); 
   return 0;
}

 

盛开吧这世界最美丽的花。