差分约束知识点

什么是差分约束：

它旨在解决不等式组求最值的问题。

就是给你一组不等式，询问你某两个变量之间的最大值or最小值

 eg：

给定n个变量和m个不等式，每个不等式形如 x[i] - x[j] <= a[k] (1<=i,j<=n, 1<=k<=m，a[k]已知)，求 x[n] - x[1] 的最大值

例 n=4，m=5 不等式组如下图

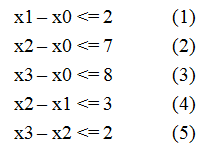
我们可以两两相加得到几个 x[4]-x[1] 的式子

1. (3) x4 - x1 <= 8

2. (2) + (5) x4 - x1 <= 9

3. (1) + (4) + (5) x4 - x1 <= 7

发现 min{8,9,7}就是我们所要求的的 x4-x1 的最大值

 差分约束中求最小值用≥，跑最长路；求最大值用≤，跑最短路

例题：

N个人编号为1-N，并且按照编号顺序排成一条直线，任何两个人的位置不重合，然后给定一些约束条件。      

 X(X <= 100000)组约束Ax Bx Cx(1 <= Ax < Bx <= N)，表示Ax和Bx的距离不能大于Cx。      

 Y(Y <= 100000)组约束Ay By Cy(1 <= Ay < By <= N)，表示Ay和By的距离不能小于Cy。

 如果这样的排列存在，输出1-N这两个人的最长可能距离，如果不存在，输出-1，如果无限长输出-2。

解：

令第x个人的位置为d[x]（不妨设d[x]为x的递增函数，即随着x的增大，d[x]的位置朝着x正方向延伸）。

那么我们可以列出一些约束条件如下：

  1、对于所有的Ax Bx Cx，有 d[Bx] - d[Ax] <= Cx；

  2、对于所有的Ay By Cy，有 d[By] - d[Ay] >= Cy；

  3、然后根据我们的设定，有 d[x] >= d[x-1] + 1 (1 < x <= N)  （这个条件是表示任何两个人的位置不重合）

 而我们需要求的是d[N] - d[1]的最大值，即表示成d[N] - d[1] <= T，要求的就是这个T

于是我们将所有的不等式都转化成d[x] - d[y] <= z的形式，如下：

    1、d[Bx]  -  d[Ax]    <=    Cx

    2、d[Ay]  -  d[By]    <=  -Cy

    3、d[x-1] -    d[x]    <=    -1

 对于d[x] - d[y] <= z，令z = w(y, x)，那么有 d[x] <= d[y] + w(y, x)，所以当d[x] > d[y] + w(y, x)，我们需要更新d[x]的值，

 这对应了最短路的松弛操作，于是问题转化成了求1到N的最短路。

 对于所有满足d[x] - d[y] <= z的不等式，从y向x建立一条权值为z的有向边。

 然后从起点1出发，利用SPFA求到各个点的最短路，如果1到N不可达，说明最短路(即上文中的T)无限长，输出-2。

 如果某个点进入队列大于等于N次，则必定存在一条负环，即没有最短路，输出-1。否则T就等于1到N的最短路。