树链剖分模板
This is hahaha

题目描述 如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作: 操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z 操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和 操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z 操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和 输入输出格式 输入格式: 第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。 接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。 接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通) 接下来M行每行包含若干个正整数,每行表示一个操作,格式如下: 操作1: 1 x y z 操作2: 2 x y 操作3: 3 x z 操作4: 4 x 输出格式: 输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模) 输入输出样例 输入样例#1: 5 2 24 3 7 8 0 2 5 1 1 4 2 2 2 5 5 1 3 1 3 输出样例#1: 21 说明 时空限制:1s,128M 数据规模: 对于30%的数据: N≤10,M≤10 对于70%的数据: N≤10^3,M≤10^3 对于100%的数据: N≤10^5,M≤10^5 ( 其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233 )
样例说明:
树的结构如下:
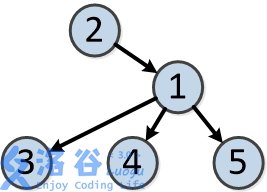
各个操作如下:
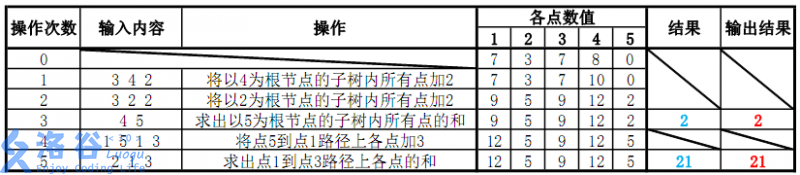
故输出应依次为2、21(重要的事情说三遍:记得取模)
正解:见标题

1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 const int N=1e5+10; 5 struct node{ 6 int v,ne; 7 }e[N*2]; 8 int h[N],tot,n,m,rt,P; 9 ll val[N],ad[N*6],sum[N*6],w[N]; 10 int dep[N],size[N],son[N]; 11 int f[N],top[N],id[N]; 12 void build(int o,int l,int r) 13 { 14 if(l==r) 15 { 16 sum[o]=w[l]%P;return; 17 } 18 int mid=(l+r)>>1; 19 build(o<<1,l,mid);build(o<<1|1,mid+1,r); 20 sum[o]=(sum[o<<1]+sum[o<<1|1])%P; 21 } 22 void down(int o,int l,int r) 23 { 24 if(ad[o]) 25 { 26 int mid=(l+r)>>1; 27 ad[o<<1]=(ad[o<<1]+ad[o])%P; 28 sum[o<<1]=(sum[o<<1]+ad[o]*(mid-l+1)%P)%P; 29 ad[o<<1|1]=(ad[o<<1|1]+ad[o])%P; 30 sum[o<<1|1]=(sum[o<<1|1]+ad[o]*(r-mid)%P)%P; 31 ad[o]=0; 32 } 33 } 34 void tadd(int o,int l,int r,int x,int y,int k) 35 { 36 if(x<=l && y>=r) 37 { 38 ad[o]=(ad[o]+k)%P; 39 sum[o]=(sum[o]+k*(r-l+1)%P)%P; 40 return; 41 } 42 down(o,l,r); 43 int mid=(l+r)>>1; 44 if(x<=mid) tadd(o<<1,l,mid,x,y,k); 45 if(y>=mid+1) tadd(o<<1|1,mid+1,r,x,y,k); 46 sum[o]=(sum[o<<1]+sum[o<<1|1])%P; 47 } 48 ll tquery(int o,int l,int r,int x,int y) 49 { 50 if(x<=l && y>=r) return sum[o]%P; 51 down(o,l,r); 52 int mid=(l+r)>>1;ll tmp=0; 53 if(x<=mid) tmp=(tmp+tquery(o<<1,l,mid,x,y))%P; 54 if(y>=mid+1) tmp=(tmp+tquery(o<<1|1,mid+1,r,x,y))%P; 55 return tmp%P; 56 } 57 void add(int u,int v) 58 { 59 tot++;e[tot]=(node){v,h[u]};h[u]=tot; 60 } 61 void dfs1(int x) 62 { 63 size[x]=1;int p=-1; 64 for(int rr,i=h[x];i;i=e[i].ne) 65 { 66 rr=e[i].v; 67 if(!dep[rr]) 68 { 69 dep[rr]=dep[x]+1;f[rr]=x; 70 dfs1(rr); 71 size[x]+=size[rr]; 72 if(size[rr]>p) p=size[rr],son[x]=rr; 73 } 74 } 75 } 76 void dfs2(int x,int up) 77 { 78 if(!x) return; 79 id[x]=++tot;top[x]=up; 80 w[tot]=val[x]; 81 dfs2(son[x],up); 82 for(int rr,i=h[x];i;i=e[i].ne) 83 { 84 rr=e[i].v; 85 if(rr!=f[x] && rr!=son[x]) dfs2(rr,rr); 86 } 87 } 88 void Qadd(int x,int y,int z) 89 { 90 while(top[x]!=top[y]) 91 { 92 if(dep[top[x]]<dep[top[y]]) swap(x,y); 93 tadd(1,1,n,id[top[x]],id[x],z); 94 x=f[top[x]]; 95 } 96 if(dep[x]>dep[y]) swap(x,y); 97 tadd(1,1,n,id[x],id[y],z); 98 } 99 ll Qquery(int x,int y) 100 { 101 ll tmp=0; 102 while(top[x]!=top[y]) 103 { 104 if(dep[top[x]]<dep[top[y]]) swap(x,y); 105 tmp=(tmp+tquery(1,1,n,id[top[x]],id[x]))%P; 106 x=f[top[x]]; 107 } 108 if(dep[x]>dep[y]) swap(x,y); 109 tmp=(tmp+tquery(1,1,n,id[x],id[y]))%P; 110 return tmp; 111 } 112 int op,x,y,z; 113 int main() 114 { 115 scanf("%d%d%d%d",&n,&m,&rt,&P); 116 for(int i=1;i<=n;++i) scanf("%lld",&val[i]); 117 for(int i=1;i<=n-1;++i) 118 { 119 scanf("%d%d",&x,&y); 120 add(x,y);add(y,x); 121 } 122 dep[rt]=1;dfs1(rt); 123 tot=0;dfs2(rt,rt); 124 build(1,1,n); 125 while(m--) 126 { 127 scanf("%d",&op); 128 if(op==1) 129 { 130 scanf("%d%d%d",&x,&y,&z); 131 Qadd(x,y,z); 132 }else if(op==2) 133 { 134 scanf("%d%d",&x,&y); 135 printf("%lld\n",Qquery(x,y)); 136 }else if(op==3) 137 { 138 scanf("%d%d",&x,&z); 139 tadd(1,1,n,id[x],id[x]+size[x]-1,z); 140 }else if(op==4) 141 { 142 scanf("%d",&x); 143 printf("%lld\n",tquery(1,1,n,id[x],id[x]+size[x]-1)); 144 } 145 // cout<<"now is ok"<<endl; 146 } 147 return 0; 148 }



