线段树基础
一,什么是线段树
线段树是一种二叉搜索树,它将一个区间划分成一些单元区间
每个单元区间对应线段树中的一个叶结点
将[1,n]分解成若干特定的子区间(数量不超过4*n)
用线段树对“编号连续”的一些点,进行修改或者统计操作,修改和统计的复杂度都是O(log2(n))
用线段树统计的东西,必须符合区间加法,
也就是说,如果已知左右两子树的全部信息,比如要能够推出父节点
否则,不可能通过分成的子区间来得到[L,R]的统计结果
一个问题,只要能化成对一些“连续点”的修改和统计问题,基本就可以用线段树来解决了
解决问题时常会用到离散化
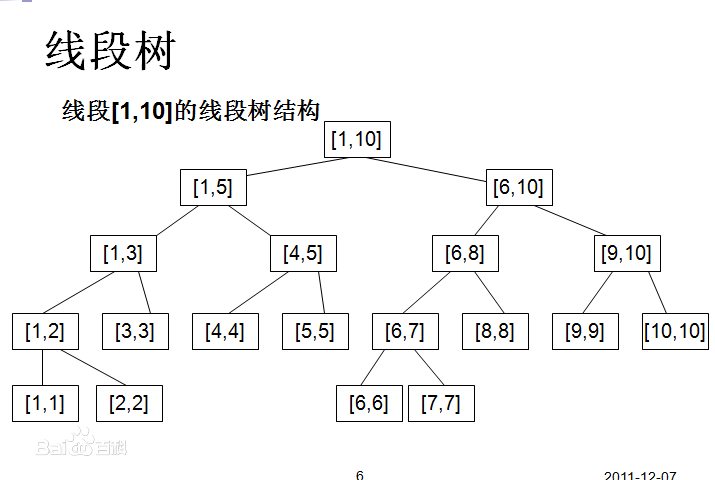
由上图可知,每个节点的左孩子区间范围为[l,mid],右孩子为[mid+1,r]
对于结点k,左孩子结点为2*k(k<<1),右孩子为2*k+1(k<<1|1)
二,线段树的一些操作
每个人的代码风格不一样,也可以写成结构体,我习惯写数组,结构体的写法和指针的写法网上有,请自行搜索
1.以线段树求和为例 题目https://www.cnblogs.com/adelalove/p/8683924.html
首先是建树
a、对于二分到的每一个结点,给它的左右端点确定范围。
b、如果是叶子节点,存储要维护的信息。
c、状态合并。

1 void build(ll o,ll l,ll r)
2 {
3 if(l==r)
4 {
5 sum[o]=a[l];
6 return;
7 }
8 ll mid=(l+r)>>1;
9 build(o<<1,l,mid);
10 build(o<<1|1,mid+1,r);
11 sum[o]=sum[o<<1]+sum[o<<1|1];
12 }
然后查询
查询某个区间的和
与二分查询法基本一致,如果当前枚举的点左右端点相等,即叶子节点,就是目标节点。
如果不是,因为这是二分法,所以设查询位置为x,当前结点区间范围为了l,r,
中点为mid,则如果x<=mid,则递归它的左孩子,否则递归它的右孩子。

1 ll query(ll o,ll l,ll r,ll x,ll y)
2 {
3 if(x<=l && y>=r)
4 {
5 down(o,l,r,(l+r)>>1);
6 return sum[o];
7 }
8 ll mid=(l+r)>>1;
9 down(o,l,r,mid);
10 ll tot=0;
11 if(x<=mid)tot+=query(o<<1,l,mid,x,y);
12 if(y>mid)tot+=query(o<<1|1,mid+1,r,x,y);
13 return tot;
14 }
区间修改
给某个区间加上某个值
重点:我们进行这个操作的时候不可能一个点一个点的改(太慢了),那怎么办呢?
我们引入一个新的状态——懒标记。
作用:存储到这个节点的修改信息,暂时不把修改信息传到子节点。你用的时候才给你,不用不给你。
实现思路(重点):
a.增加新的变量,存储这个懒标记。
b.递归到这个节点时,只更新这个节点的状态,并把当前的更改值累积到标记中。
注意是累积,可以这样理解:过年,很多个亲戚都给你压岁钱,但你暂时不用,所以都被你父母扣下了。
c.什么时候才用到这个懒标记?当需要递归这个节点的子节点时,标记下传给子节点。
这里不必管用哪个子节点,两个都传下去。就像你如果还有妹妹,父母给你们零花钱时总不能偏心吧
d.下传操作:
①当前节点的懒标记累积到子节点的懒标记中。
②修改子节点状态。即子节点继承父亲节点的标记
③父节点懒标记清0。这个懒标记已经传给子节点了,父节点的就没必要存在了。

1 void down(ll o,ll l,ll r,ll mid) 2 { 3 if(add[o]) 4 { 5 add[o<<1]+=add[o]; 6 sum[o<<1]+=add[o]*(mid-l+1); 7 8 add[o<<1|1]+=add[o]; 9 sum[o<<1|1]+=add[o]*(r-(mid+1)+1); 10 11 add[o]=0; 12 } 13 }

1 void up(ll o,ll l,ll r,ll x,ll y,ll k) 2 { 3 if(x<=l && y>=r) 4 { 5 add[o]+=k; 6 sum[o]+=k*(r-l+1); 7 return; 8 } 9 ll mid=(l+r)>>1; 10 down(o,l,r,mid); 11 if(x<=mid)up(o<<1,l,mid,x,y,k); 12 if(y>=mid+1)up(o<<1|1,mid+1,r,x,y,k); 13 sum[o]=sum[o<<1]+sum[o<<1|1]; 14 }


