201871030119-马桂婷 实验二 个人项目—《折扣0-1背包问题》项目报告
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 2018卓越工程师班 |
| 这个作业要求链接 | 软件工程个人项目 |
| 我的课程学习目标 | 1、掌握软件项目个人开发流程; 2、掌握Github发布软件项目的操作方法。 |
| 这个作业在哪些方面帮助我实现学习目标 | 1、对软件项目个人开发流程有了初步的了解; 2、熟悉了GitHub的使用。 |
| 项目Github的仓库链接地址 | GitHub源代码仓库 |
-
任务一:阅读教师博客“常用源代码管理工具与开发工具”内容要求,点评班级博客中已提交相关至少3份作业
-
任务二:详细阅读《构建之法》第1章、第2章,掌握PSP流程
通过再一次的阅读《构建之法》第一、二章,我对PSP(个人软件开发流程)有了一定的理解与掌握。首先,PSP是一种可以用于控制、管理和改进个人工作方式的自我持续改进过程,是一个包括软件开发表格、指南和规程的结构化框架。在《构建之法》中,通过三个不同的表格向我们展示了PSP的各个版本以及具体的内容,通过表格可以看到PSP能够帮助软件工程师对某一个软件项目做出一个比较精确的计划以及用时估计。
PSP可以帮助一个软件工程师明确一个软件产品为了改进其质量而做出的具体步骤。在软件工程师接到一个项目时,首先将这个项目划分成几个较小的模块,同时可以估计要完成各个模块所花费的时间,然后再将各个模块进行更细致的划分,将每一项任务完成所需的时间估计出来,这样就可以相对较为合理的安排工程师的工作时间以及项目模块的完成。这样不仅可以使软件工程师有较为合理的安排,同时还可以建立一个度量在个人软件开发流程中改善的基准,提高软件工程师的工作能力。
在《构建之法》这本书中,表2-3向我们展示了一个软件工程师在完成一个软件项目时所要完成的任务清单。首先,将项目划分为三个模块,分别是计划、开发和报告。顾名思义,计划就是对这个项目有一个初步的计划,具体就是计算一下完成这个项目所需要的大概时间;开发则是完成这个项目的核心部分,首先要根据实际要求有一个需求分析,然后生成一个设计文档,完成后还要和同事一起对这个设计文档有一个审核过程,完成后为该项目开发制定一个代码规范,接下来就可以进入到项目的具体开发阶段了,对项目有一个初步的设计,然后按照设计展开进行项目的编码工作,完成后需要对代码进行代码复审,这个过程可以帮助工程师及早的发现存在的缺陷,使修复缺陷的代价最小,复审完成后便可开始测试工作,测试通过后整个开发阶段就完成了;开发完成后,剩下的就是报告阶段,首先对完成的工作有一个完成记录的时间计算,接下来就可以完成测试结果的相应报告,完成后就可以对所完成的工作有一个工作量的计算,所有以上工作完成后就可以总结一下此次工作的经验以及不足之处,然后提出对这样一个个人软件开发流程中不足之处的改进计划。这样整个个人软件开发流程就全部完成了。
-
任务三:项目开发
-
需求分析:
背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?
D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式,用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解,达到获利最大化。D{0-1}KP数据集由一组项集组成,每个项集有3项物品可供背包装入选择,其中第三项价值是前两项之和,第三项的重量小于其他两项之和,算法求解过程中,如果选择了某个项集,则需要确定选择项集的哪个物品,每个项集的三个项中至多有一个可以被选择装入背包,D{0-1} KP问题要求计算在不超过背包载重量 的条件下,从给定的一组项集中选择满足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大;D{0-1}KP instances数据集是研究D{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。
在这里首先需要用到读取文件的相关操作用以将实验数据导入到程序中,我选择用Python来完成数据的读入以及数据的提取工作;其次,题目中提到要用动态规划算法以及回溯法来求解D{0-1}KP,所以还需要再巩固一下之前所学过的动态规划算法、回溯算法以及0-1背包问题的求解过程;最后,根据需要完成的基本功能来看,还需要去了解一下python的数据可视化等相关知识。
-
功能设计:
基本功能:
a.可正确读入实验数据文件的有效D{0-1}KP数据;
b.能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
c.能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
d.用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位);
e.任意一组D{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
-
设计实现:
由于本次实验对我来说比较有难度,所以其中要求的基本功能完成的情况不是很好,散点图部分最初只是在单独的程序中画了出来,后来通过网上查阅资料又重新在完整的程序中完成了这项内容。
-
提取数据:在浏览题目的时候,由于看到了有散点图的绘制,所以选择用python作为此次项目的开发语言,但是由于对python的学习还不够,导致整个项目的第一步提取数据就出现了问题,在数据的提取这一部分还不够完善,有手动输入的部分。
-
散点图绘制:散点图的绘制主要是导入了画图模块,也就是python的一个库,即matplotlib,它是必备的数据可视化工具,其中包含了大量的工具,可以绘制各种图形,当然也包括我们所要绘制的散点图。在这一部分的完成中,起初由于数据的提取工作没有很好地完成,所以这一步最开始没有提取数据,而是将数据直接写在程序中得到的散点图。但是后来又找到了一个读取数据的方法,虽然不是很完善,但还是可以实现要求的基本功能,所以在这一步中首先是将第一步中提取到的数据转换为int类型,然后进行散点图的绘制。
-
价值:重量比排序:在前两步基本完成之后,这一步就变得比较简单了,这一部分的完成中,我首先是将价值和重量比的所有项集都比出来,然后将第三个项都提取出来,得到最终排序的结果。
-
最优解和求解时间:这一部分内容我只完成了用动态规划算法求解背包问题的过程,用回溯算法求解的过程最终没能写出来。动态规划算法的部分首先是将物品的重量以及对应的价值放进一个二维列表,然后遍历列表将得到的每一个物品所对应的最大质量得到,最终得到最优解。求解时间是用了python中的时间函数模块来完成的。
-
保存为txt文件或导出EXCEL文件:这一部分内容是用了文件中的write函数来完成的。
-
-
测试运行:
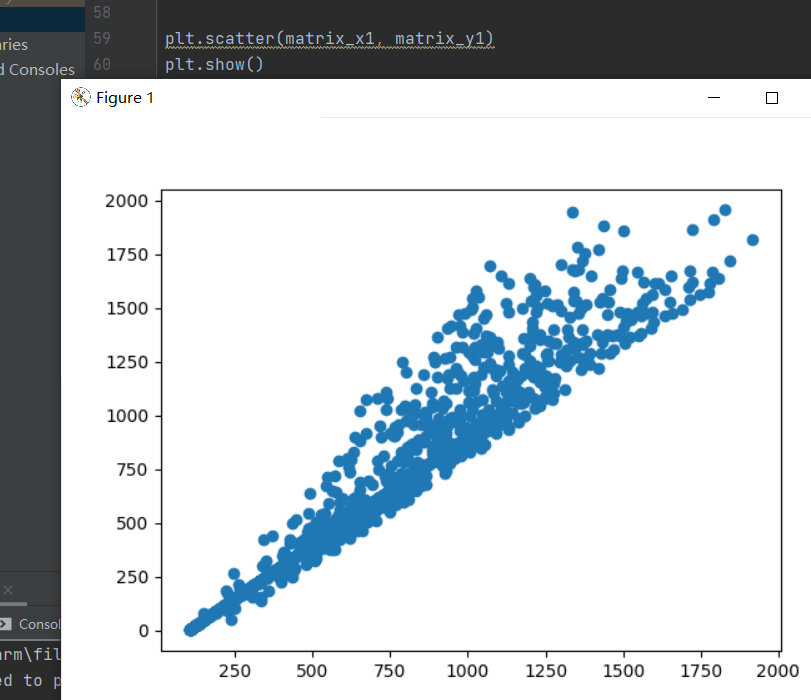
![3*400的数据组单独测试]()
3*400的数据组单独测试
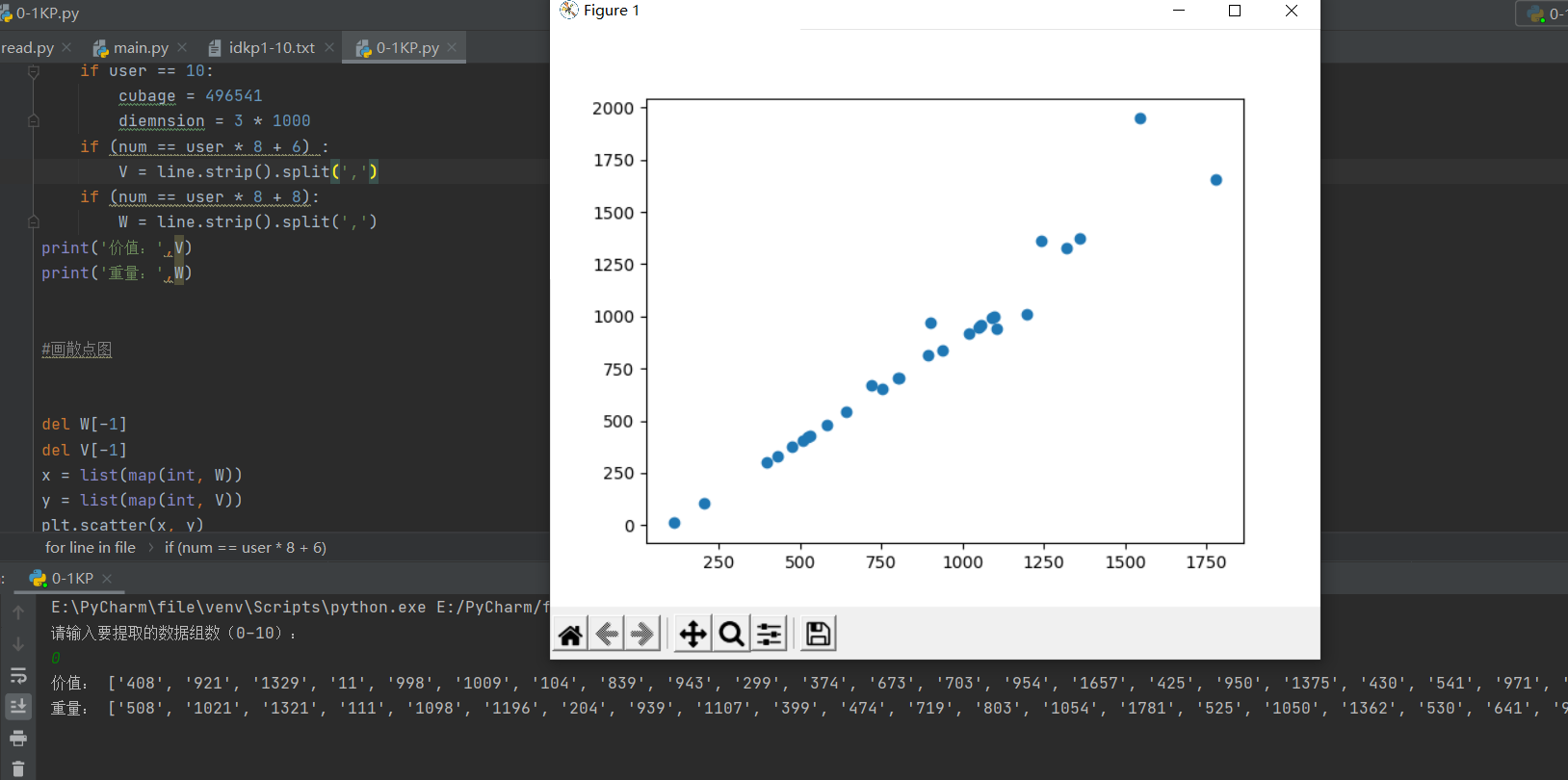
![3*10的数据组测试]()
3*10的数据组测试
![数据提取及排序结果测试]()
数据提取及排序结果测试
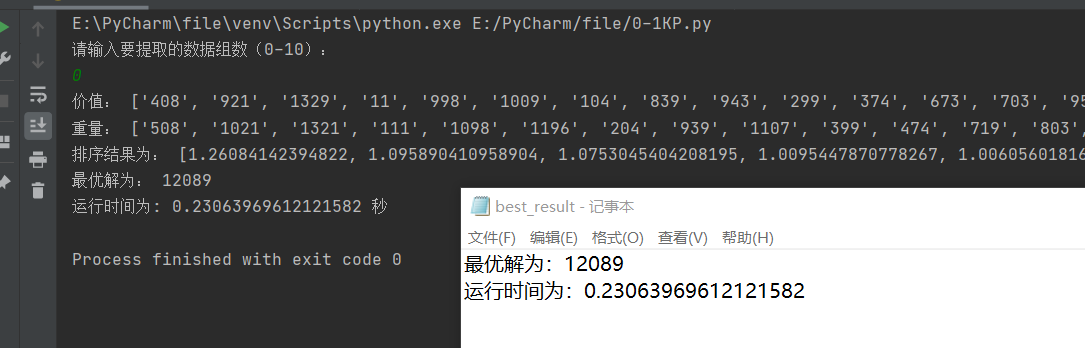
![总的结果]()
所有内容完成的运行结果
-
独特/满意的代码片段:
1、项集第三项的价值:重量比的非递增排序代码如下:
#项集第三项的价值:重量比的非递增排序 Ratio = [] #项集所有项比值 Ratio_1 = [] #第三项比值排序 n = len(x) for i in range(n): #将项集的所有项比值存入Ratio ratio = y[i]/x[i] Ratio.append(ratio) for i in range(2, len(Ratio), 3): #将第三项的比值存入Ratio_1 ratio_1 = Ratio[i] Ratio_1.append(ratio_1) Ratio_1.sort(reverse=True) #排序 print('排序结果为:',Ratio_1)2、绘制散点图的代码如下:
#画散点图 del W[-1] del V[-1] x = list(map(int, W)) #将字符型转换为整形 y = list(map(int, V)) plt.scatter(x, y) #画散点图 plt.show() #print(x)3、动态规划实现0-1背包问题的求解
for i in range(len(bag)): best.append([0]*(m+1)) for i in range(m+1): if i >= bag[0][1]: best[0][i] = bag[0][0] #第一次遍历数组将得到第一个物品所对应的最大质量得出 for i in range(1, len(bag)): for j in range(m+1): if bag[i][1] <= j: best[i][j] = max(best[i-1][j], best[i-1][j-bag[i][1]]+bag[i][0]) # 取best[i][j]当前的最大质量 -
总结:
软件设计的“模块化”原则就是用特定的程序段做特定的事,不是将一个项目一股脑的从头写到尾,而是尽量将其划分为多个可分解的模块,使每个模块都可以用函数来实现,自己编写相应的函数来实现这一功能,完成每个模块对应的函数之后就可以直接在main函数中调用其他自定义的函数来解决问题。但在本次实验中,由于没有按照要求完成老师布置的任务,所以在整个实验的过程中并没有实现使用“模块化”的原则来完成本次任务,而是直接将各个任务划分开来,单独的写成了一个程序。
-
展示PSP:
PSP2.1 任务内容 计划共完成需要的时间(min) 实际完成需要的时间(min) Planning 计划 60 80 · Estimate · 估计这个任务需要多少时间,并规划大致工作步骤 60 80 Development 开发 1360 1050 ·· Analysis 需求分析 (包括学习新技术) 300 240 · Design Spec · 生成设计文档 180 · Design Review · 设计复审 (和同事审核设计文档) 60 · Coding Standard 代码规范 (为目前的开发制定合适的规范) 20 10 · Design 具体设计 180 160 · Coding 具体编码 500 600 · Code Review · 代码复审 60 · Test · 测试(自我测试,修改代码,提交修改) 60 40 Reporting 报告 100 20 ·· Test Report · 测试报告 60 · Size Measurement 计算工作量 10 · Postmortem & Process Improvement Plan · 事后总结 ,并提出过程改进计划 30 20
-
-
任务四:完成任务三的程序开发,将项目源码的完整工程文件提交到注册的GitHub账号的项目仓库中
GitHub的账号注册已在实验一中完成,在该实验中创建了用于存放该项目代码的仓库项目仓库链接地址,第一次正式使用GitHub,所以还不是很熟悉,有些地方可能还有问题,所以接下来还需要好好熟悉一下具体的使用方法。
实验总结:相比于前两次的实验,这次实验的难度要有很大的难度,可能也是我自身的原因,在看到这样一个项目之后第一感觉就是无从下手,不只是因为这个项目本身就是一个比较大的工程。虽然现在已经是三年级的计算机专业学生了,但知道我的专业知识能力与我的实际学习时间并不匹配,通过这个实验就可以很好地证明这一点。但是对于落下的东西也不能就此放弃,所以在本次实验中虽然没有很好地完成相关要求,但还是学到了一点相关的知识,比如python的数据可视化的相关知识,同时对于之前了解比较浅薄的一点python知识也进行了复习。这只是一个开始,我已经意识到过去的学习存在着很多并且很大的问题,所以在接下来的学习中,需要花费一些时间去加深对相关专业知识的理解与学习,争取在之后类似这样的作业中能有一个比较满意的实验结果。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号