决策树

决策树

决策树是机器学习里面一个比较简单的模型。决策树学起来比较简单，思路也很明确，但是，如果深入了解，还是有很多可以讲的地方的。Random Forest，GBDT，XGBOOST等等，都是决策树的扩展。

什么是决策树

顾名思义，决策树是基于树结构来进行决策的，这与人们面临真实的决策问题时的处理过程类似。这个决策过程类似下图所示。

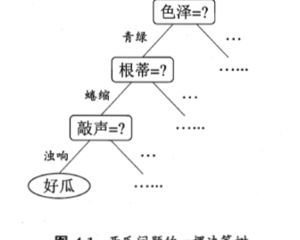
划分选择

决策树学习的关键是如何选择最优化分属性。一般而言，随着划分过程不断进行，我们希望分支结点所包含的样本尽可能属于同一类别，也就是“纯度”越来越高。

信息增益（ID3）

信息熵（Information Entropy）是度量样本集合纯度最常用的一种指标。假定当前样本集合\(D\)中，第\(k\)类样本所占比例为\(p_k\)，则信息熵定义如下：

\[Entropy(D)= - \sum_k {p_k}\log_2{p_k} \]

\(Entropy(D)\)的值越小，则D的纯度越高。

有了这一衡量标准，那么就可以选择信息增益最大的划分方式。假定离散变量\(a\)有\(V\)个可能的取值，则\(D^v\)的信息熵为：

\[Entropy(D,a) = \sum_{v \in V} \frac{|D^v|}{|D|} Entropy(D^v) \]

该划分的信息增益为：

\[Gain(D,a) = Entropy(D) - Entropy(D,a) \]

因此，最佳的特征为：

\[a_* = \mathop{\arg\max}_{a \in A} Gain(D,a) \]

通过该策略构建的决策树，就是最经典的ID3算法。

信息增益率（C4.5）

在ID3算法中，没有考虑划分的复杂性，具体来说，如果一个特征有大量的可选取值，对应每条记录的取值都不用，那么按该特征划分的结果就是100%正确了。显然，这个决策树是不具备泛化能力的，无法对新样本进行有效预测。

实际上，信息增益对于可取数值较多的属性有所偏好，为减少这种偏好，C4.5算法引入了信息增益率来选择最优划分属性。增益率的定义如下：

\[Gain\_ratio(D)= \frac{Gain(D,a)}{IV(a)} \]

其中

\[IV(a)=- \sum_{v \in V} \frac{|D^v|}{|D|} \log_2 \frac{|D^v|}{|D|} \]

Gini系数（CART）

CART算法和ID3算法不同，采取Gini系数来度量划分的纯度：

\[\begin{align} Gini(D) & = \sum_k \sum_{k' \neq k} p_k p_{k'} \\ & = 1 - \sum_{k} p_k^2 \end{align} \]

直观来说，\(Gini(D)\)系数反应了从数据集中随机抽取两个样本，其类别标记不一致的概率。因此，Gini系数越小，数据集的纯度越高。属性a的基尼系数定义如下：

\[Gini\_index(D,a)=\sum_{v \in V}\frac{|D^v|}{|D|}Gini(D^v) \]

则，最优的划分方式为：

\[a_* = \mathop{\arg\min}_{a \in A} Gini\_index(D,a) \]

剪枝处理

对于决策树而言，很容易出现过拟合现象，比如树的过度生长。因此，可以通过主动去掉一些分支来降低过拟合的风险。决策树剪枝的基本策略有“预剪枝”和“后减枝”。

预剪枝

在划分之前，所有样例集中在根节点，其类别标记为训练集样例数最多的类别，此时可以求得其在验证集上的分类准确率\(acc\) 。之后，在划分标准a下，得到生长的决策树模型的准确率\(acc'\)。如果，\(acc < acc'\)，则说明划分效果不好，因此丢弃当前分支，不再向下生长。

后减枝

后减枝与预剪枝的思想相似，但剪枝的过程在决策树构建完成之后。与预剪枝相比，后剪枝得到的决策树往往会更复杂，避免了预剪枝下决策树过度简单所导致的模型欠拟合。但是，由于后减枝是在决策树构建完成之后，因此，大量的节点的计算是无效的，对资源的浪费较大。

一般形式

决策树的剪枝往往是通过极小化决策树整体的损失函数来实现的。

\[C(T)=\sum_{t=1}^T N_t H_t(T) \]

其中，\(N_t\)表示叶节点样本，\(H_t\)表示该节点上的信息熵。

上述的损失函数中，仅仅考虑了经验风险，为了考虑模型的结构风险，引入模型复杂度\(|T|\)。

\[C(T)=\sum_{t=1}^T N_t H_t(T) + \alpha |T| \]

一般而言，模型的复杂度可以使用叶节点的个数来简单衡量，通过加大\(\alpha\)的值，可以得到一个更加简洁的树结构。

总结

和之前的逻辑回归相比，决策树更加的简明易懂。由决策树发展而来的复杂树模型也是数据分析中常用的模型。更值得一提的，决策树采用的信息论的思想，能帮助我们更好的选择模型特征。