逻辑回归

逻辑回归是统计学习方法中的经典分类方法，也是在深度学习兴起之前，工业界最为常用的分类算法之一。

什么是逻辑回归

逻辑回归在某些书中也被称为对数几率回归（比如西瓜书），是一种广义的线性模型：利用一个单调可微的函数将分类任务的真实标记 $ y $ 与线性回归模型的预测值联系起来。

考虑一个二分类问题，输入为 $ y \in {0,1 } $ ，而线性回归模型产生的预测值为，而线性回归模型产生的预测值为，而线性回归模型产生的预测值为，而线性回归模型产生的预测值为 ，而线性回归模型产生的预测值为，而线性回归模型产生的预测值为，而线性回归模型产生的预测值为 ，而线性回归模型产生的预测值为\(z=w^Tx+b\)是实数值，因此，需要找到一个可以将实值转化为0/1值得阶跃函数。最理想的是“单位阶跃函数”。

\[y = \left\{ \begin{aligned} 0&, & z<0\\ 0.5&,&z=0\\ 1&,&z>0 \end{aligned} \right. \]

但是，该函数不连续，我们希望有一个单调可微的函数来代替，因此找到了Sigmoid function。

\[Sigmoid : y=\frac{1}{1+e^{-z}} \]

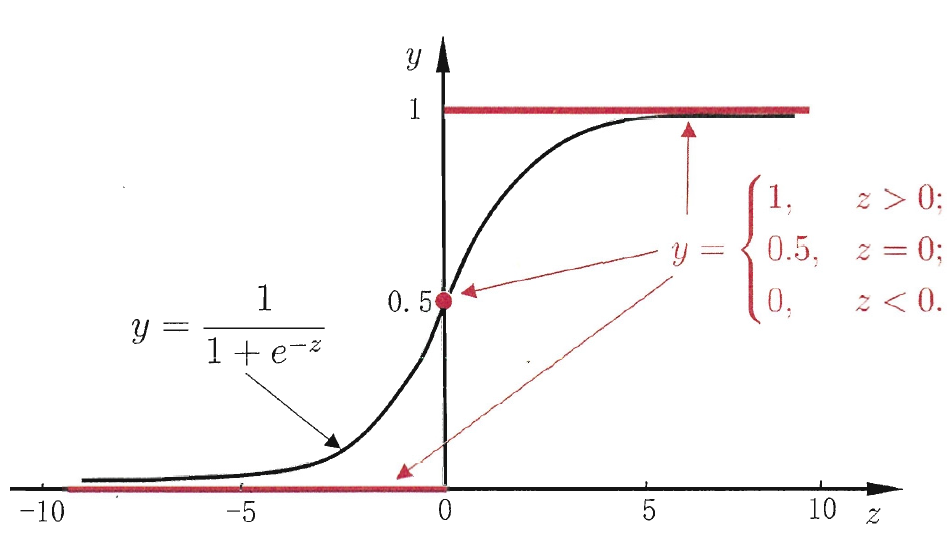
从图中可以看出，Sigmoid函数将z值转化为接近于0或1的y值，并且输出值在z=0附近变化很陡。由于其取值在[0,1]中，可以将其视为正类的后验概率估计\(p(y=1|x)\)。

\[\widehat{y}=\left\{ \begin{aligned} 1&,&if\phi(z)\ge0\\ 0&,&otherwise \end{aligned} \right. \]

代价函数

如果将\(\phi(z)\)可以视为类1的后验概率，所以我们有：

\[\begin{align} p(y=1|x;w)&=\phi(w^Tx+b)=\phi(z)\\ p(y=0|x;w)&=1-\phi(z) \end{align} \]

其中，\(p(y=1|x;w)\)表示给定\(w\)，在\(x\)的情况下，\(y=1\)的概率大小。

上面的两个式子可以写为一般形式

\[p(y|x;w)=\phi(z)^y(1-\phi(z))^{(1-y)} \]

接下来，就可以使用极大似然估计来根据给定的训练集估计出参数\(w\)。

\[L(w)=\prod^n_{i=1}p(y^i|x^i;w)=\prod^n_{i=1}\phi(z^i)^{y^i}(1-\phi(z^i))^{(1-y^i)} \]

为了简化运算，对上式两边取对数：

\[l(w)=lnL(w)=\sum^n_{i=1}y^{i}ln(\phi(z^i))+(1-y^i)ln(1-\phi(z^i)) \]

接下来，我们的目标就是求使\(l(w)\)最大化的\(w\)。更一般的，在\(l(w)\)之前添加符号，就变成了求最小值，也就是代价函数。

\[J(w)=-l(w)=-\sum^n_{i=1}y^{i}ln(\phi(z^i))+(1-y^i)ln(1-\phi(z^i)) \]

求解参数

首先介绍一下Sigmoid function的导数：

\[\phi'(z)=\phi(z)(1-\phi(z)) \]

接下来，需要明确一点，梯度的负方向就是代价函数下降最快的方向。基于此，便可以优化参数了。

\[\begin{align} \bigtriangledown J(w_j) &= \frac{\partial J(w)}{\partial w_j}\\ \bigtriangleup w &= -\eta \bigtriangledown J(w)\\ w&=w+\bigtriangleup w \end{align} \]

对于逻辑回归而言：

\[\begin{align} \frac{\partial J(w)}{\partial w_j}&=-\sum^n_{i=1}(y^i\frac{1}{\phi(z^i)}-(1-y^i)\frac{1}{1-\phi(z^i)})\frac{\partial\phi(z^i)}{\partial w_j}\\ &=-\sum^n_{i=1}(y^i\frac{1}{\phi(z^i)}-(1-y^i)\frac{1}{1-\phi(z^i)})\phi(z^i)(1-\phi(z^i))\frac{\partial z^i}{w_j}\\ &=-\sum^n_{i=1}(y^i(1-\phi(z^i)) - (1-y^i)\phi(z^i))x^i_j\\ &=-\sum^n_{i=1}(y^i-\phi(z^i))x^i_j \end{align} \]

所以，权重更新公式如下：

\[w_j=w_j+\eta\sum^n_{i=1}(y^i-\phi(z^i))x^i_j \]

注意事项

1.样本含量

在模型训练时，样本量应该取多少一直是一个令人困惑的问题。根据某些专家的经验，如果样本量少于100，Logistic回归的最大似然估计可能会有一定的风险，如果大于500，则显得比较充足。当然，样本大小还依赖于变量个数、数据结构等条件。（一般认为，每一个自变量至少要10例结局保证估计的可靠性。注意：这里是结局例数，而不是整个样本例数。如果你有7个自变量，那至少需要70例研究结局，否则哪怕你有1000例，而结局的例数只有10例，依然显得不足。）

2.关于自变量形式

理论上，Logistic回归中的自变量可以是任何形式，定量资料和定性资料均可。但在数据分析时通常更倾向于自变量以分类的形式进入模型，因为这样更方便解释。

3.关于标准误过大的问题

对于此类问题，可能有以下原因：

• 该变量某一类的例数特别少，如性别，男性有100人，女性有2人，可能会出现这种情形。
• 空单元格（zero cell count），如性别与疾病的关系，所有男性都发生了疾病或都没有发生疾病，这时候可能会出现OR值无穷大或为0的情形。
• 完全分离（complete separation），对于某自变量，如果该自变量取值大于某一值时结局发生，当小于该值时结局都不发生，就会出现完全分离现象。如年龄20、30、40、50四个年龄段，如果40岁以上的人全部发生疾病，40岁以下的人全部不发病，就产生了完全分离现象，也会出现一个大得不可理喻的标准误差。
• 多重共线性问题，多重共线性会产生大的标准误差。

几个错误的做法

1.多分类变量不看其与logitP的关系直接进入模型

有时候你会发现某些多分类自变量应该有意义但怎么也得不到有统计学意义的结果，那你最好看一下这些自变量与logitP是神马关系，是直线关系吗？如果不是，请设置虚拟变量（SPSS叫做哑变量）后再进入模型。

2.参数估计无统计学意义

有时候会发现所有自变量参数估计均无统计学意义，如果你认为不大可能所有自变量都无统计学意义，那可以看下是不是标准误太大导致的Wald卡方检验失效，如果是，不妨换用似然比检验重新分析。

3.只看参数检验结果

Logistic回归中有很多指标可用于拟合优度的评价，如Pearson卡方、Deviance、AIC、似然比统计量等。

参考资料

1. https://www.jianshu.com/p/15646e157fbd
2. https://blog.csdn.net/zjuPeco/article/details/77165974
3. 周志华. 机器学习[M]. 清华大学出版社, 2016.