聚类算法——MCL

最近在看聚类方面的论文，接触到了MCL聚类，在网上找了许久，没什么中文的资料，可能写的最具体的便是GatsbyNewton写的 马尔可夫聚类算法（MCL） 这篇博客了。但是，其中仍有一些不详细的地方。而MCL这一方法是在作者在其博士论文中提出的，篇幅太长，难以细读，也不适合作为用来学习MCL这一算法的文献。找来找去，终于找到一篇可以看的PDF文档，但每中不足的是此文档是英文的。趁此机会，结合上述材料，总结了一下MCL的基本思想，也为了往个人博客里添加些实质性的内容，便整理了这一文档。文章中可能会有不对的地方，希望大家相互交流 ｡◕‿◕｡

Background

Different Clustering

Vector Clustering

我们在描述一个人时，常常会使用他所拥有的特点来表示，比如说：张三，男，高个子，有点壮。那么，这就可以用四维向量来表示，如果再复杂一些，就是更高维的向量空间了。下图是在二维空间之中的分布情况，可以较为直观的看出，以红色虚线为界，可以分为两个类别。

Graph Clustering

和特征聚类不同，图聚类比较难以观察，整个算法以各点之间的距离作为突破口，可以这样形容：张三，是王五的好朋友，刚认识李四，对赵六很是反感。那么，对于该节点，我们无法直接得出他的特征，但能知道他的活动圈。利用图聚类，可以将同一社交范围的人聚合到一起。MCL就是属于图聚类的一种。

Random Walks

首先看下图：

从图中，我们可以看到，不同的簇，应当具有以下的特点：

• 位于同一簇的点，其内部的联系应当紧密，而和外部的联系则比较少（惺惺相惜）

也就是说：如果你从一个点出发，到达其中的一个邻近点，那么你在簇内的可能性远大于离开当前簇，到达新簇的可能性——这就是MCL的核心思想。如果在一张图上进行多次的“Random Walks”，那么就有很大可能发现簇群，达到聚类的目的。而“Random Walks”的实现则是通过“Markov Chains”（马尔柯夫链）。

Markov Chains

为了说明 Markov Chain ，我们使用如下的简单例子：

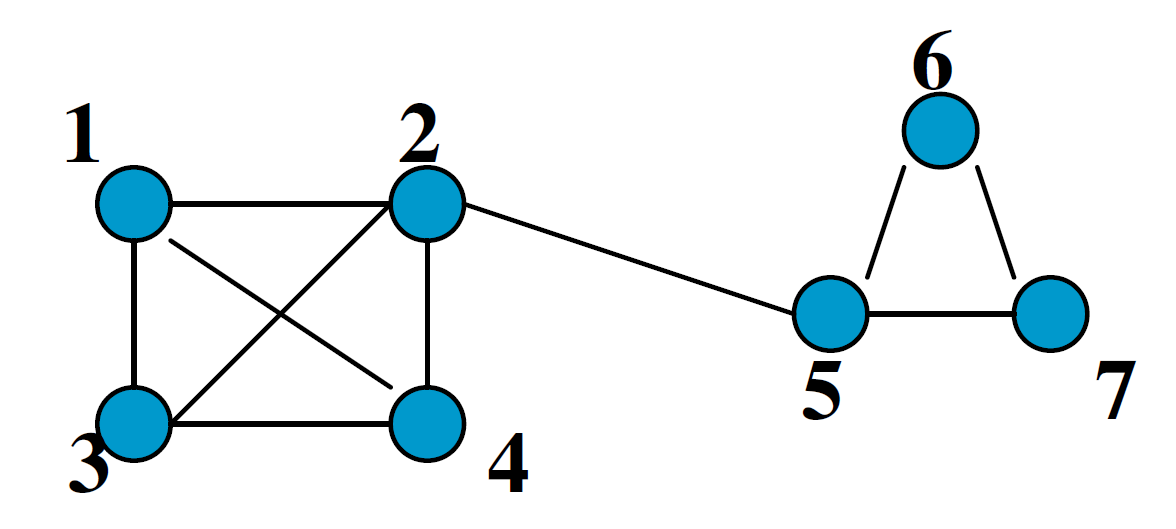
在此图中，我们可以分为两个子图：$V(1,2,3,4)$和$V(5,6,7)$，其中，$V_1$是一簇，$V_2$是另一簇。在同一簇群中，各点之间完全连接，在不同簇之间，仅有$(2,5)$一条边。

• 现在，我们从$V_1$出发，假设每条边都一样，那么则一步之后我们有$1/3$的概率到达$V_2$，$1/3$的概率到达$V_3$，$1/3$的概率到达$V_4$，同时，有0的概率到达$V_5,V_6,V_7$。
• 对于$V_2$，则有$1/4$的概率到达$V_1,V_3,V_4,V_5$，有0的概率到达$V_6,V_7$。

通过计算每个点到达其余点的概率，我们可以得到如下的概率矩阵：

$$P = \left[ \matrix{ 0 & .25 & .33 & .33 & 0 & 0 & 0 \cr .33 & 0 & .33 & .33 & .33 & 0 & 0 \cr .33 & .25 & 0 & .33 & 0 & 0 & 0 \cr .33 & .25 & .33 & 0 & 0 & 0 & 0 \cr 0 & .25 & 0 & 0 & 0 & .5 & .5 \cr 0 & 0 & 0 & 0 & .33 & 0 & .5 \cr 0 & 0 & 0 & 0 & .33 & .5 & 0 } \right]$$

为了计算简单，我们使用一个更简单的矩阵进行接下来的说明：

$$P_1 = \left[ \matrix{ .6 & .2 \cr .4 & .8 } \right]$$

这表示的是从任意点出发，经过一步之后到达其它点的概率矩阵，那么，经过两次之后、三次以及最终的概率矩阵为：

$$P_2 = P_1P_1 \left[ \matrix{ .44 & .28 \cr .56 & .72 } \right] \\ P_3 = P_2P_1 \left[ \matrix{ .35 & .32 \cr .65 & .68 } \right] \\ \vdots \\ P_n = \left[ \matrix{ .33 & .33 \cr .66 & .66 } \right]$$

根据上述例子，我们已经接触到了 Markov Chain ，那么现在就给其下一个定义：

Markov Process——在给定当前知识或信息的情况下，过去（即当期以前的历史状态）对于预测将来（即当期以后的未来状态）是无关的。

Markov Chain——如果有由随机变量$X_1,X_2,X_3\cdots$组成的数列。这些变量的范围，即他们所有可能取值的集合，被称为“状态空间”。而$X_n$的值则是在时间$n$的状态，如果$X_{n+1}$对于过去状态的条件概率分布满足：$P(X_{n+1} = x | X_0,X_1,X_2,\cdots,X_n) = P(X_{n+1} = x | X_n)$，则我们称其是一条Markov Chain

Weighted Graphs

之前的例子中，图的边是没有权值的，也就是所有的边都是一样的。现在，为每条边添加一个权重（可以理解为亲密程度），那么，就需要重新计算到达每个点的概率了。

假设有如下的图：

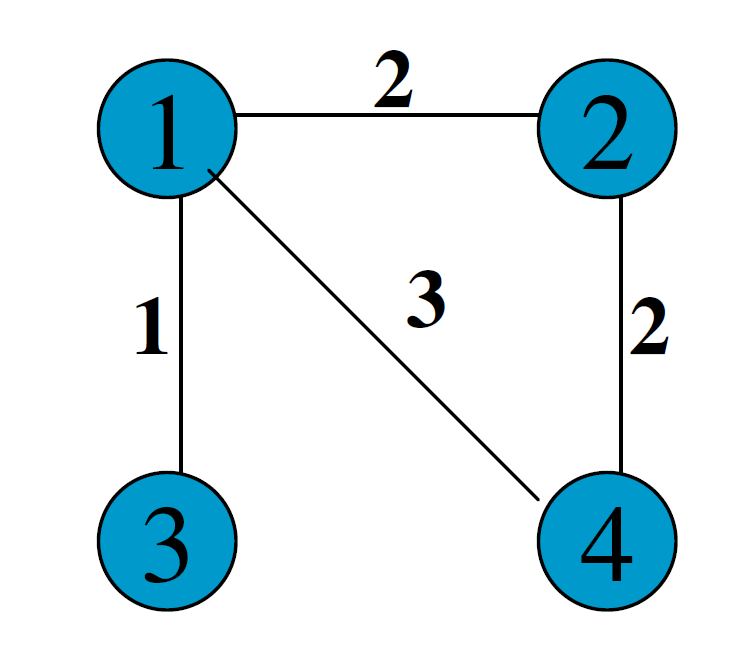
那么，其概率矩阵怎么计算？

首先，我们要计算得到邻接矩阵，即：

$$edge = \left[ \matrix{ 0 & 2 & 1 & 3 \cr 2 & 0 & 0 & 2 \cr 1 & 0 & 0 & 0 \cr 3 & 2 & 0 & 0 } \right]$$

通过邻接矩阵，我们就可以计算得到概率矩阵了，具体计算公式如下：

$$P_{ij}=\frac{edge_{ij}}{\sum\limits_{i=1}^{n}{edge_{ij}}}$$

最后的概率矩阵如下：

$$P = \left[ \matrix{ 0 & 1/2 & 1 & 3/5 \cr 1/3 & 0 & 0 & 2/5 \cr 1/6 & 0 & 0 & 0\cr 1/2 & 1/2 & 0 & 0 } \right]$$

之后的计算相同。

Self Loops

在上述的例子中均未考虑一个重要的问题，我们先来看一个例子：

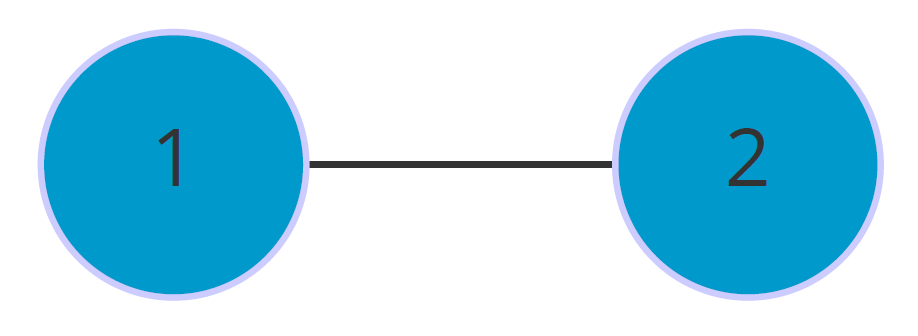
很简单，就两个点，一条边。那么，它的概率矩阵呢：

$$P_{odd} = \left[ \matrix{ 0 & 1 \cr 1 & 0 \cr } \right] \\ P_{even} = \left[ \matrix{ 1 & 0 \cr 0 & 1 \cr } \right]$$

仔细观察可以发现，这个概率矩阵不管进行几次计算，都不会收敛，而且，对于$P_{11}$和$P_{22}$而言，仅在奇数步后到达，在偶数步时，永远不可达。因此，无法进行随机游走（本来它就没有随机项供人选择）

为了解决这个问题，我们可以为其添加自环来消除奇偶幂次带来的影响：

$$edge = \left[ \matrix{ 1 & 1 \cr 1 & 1 \cr } \right] \\ P = \left[ \matrix{ .5 & .5\cr .5 & .5 } \right]$$

MCL

Markov Chain Cluster Structure

利用 Random Walks 可以求出最终的概率矩阵，但是，在求的过程中，也丢失了大量的信息。

还是这张图，它的概率矩阵和最终的概率矩阵如下：

$$P = \left[ \matrix{ 0 & .25 & .33 & .33 & 0 & 0 & 0 \cr .33 & 0 & .33 & .33 & .33 & 0 & 0 \cr .33 & .25 & 0 & .33 & 0 & 0 & 0 \cr .33 & .25 & .33 & 0 & 0 & 0 & 0 \cr 0 & .25 & 0 & 0 & 0 & .5 & .5 \cr 0 & 0 & 0 & 0 & .33 & 0 & .5 \cr 0 & 0 & 0 & 0 & .33 & .5 & 0 } \right] \Longrightarrow \left[ \matrix{ .15 & .15 & .15 & .15 & .15 & .15 & .15 \cr .2 & .2 & .2 & .2 & .2 & .2 & .2 \cr .15 & .15 & .15 & .15 & .15 & .15 & .15 \cr .15 & .15 & .15 & .15 & .15 & .15 & .15 \cr .15 & .15 & .15 & .15 & .15 & .15 & .15\cr .1 & .1 & .1 & .1 & .1 & .1 & .1\cr .1 & .1 & .1 & .1 & .1 & .1 & .1 & } \right]$$

从最终的矩阵可以看出，其最终概率和起始点的位置无关！对于聚类，这并不是一个好消息，因为我们想要得到的是一个有明显区分度的矩阵来表示不同的类别。因此，我们需要对其进行一定的修改，这也是MCL主要要解决的问题。

Inflation

如果说，前面的内容在介绍 Markov Chain 如何进行 Expansion 的话，那么，现在就添加一个新的过程： Inflation 。这个过程就是为了解决 Expansion 所导致的概率趋同问题的。

简单的说，Inflation 就是将概率矩阵中的每个值进行了一次幂次扩大，这样就能使得强化紧密的点，弱化松散的点。（强者恒强，弱者恒弱）

假设有矩阵$M^{k \times l}$，和一个给定的非负实数$r$，经过 Inflation 强化后的矩阵为$\Gamma_rM$，那么它的强化公式如下：

$$(\Gamma_rM)_{pq} = (M_{pq})^r / \sum\limits_{i=1}^k (M_{pq})^r$$

为了更直观的说明，我们来看下面的一个例子：

$$A = \left[ \matrix{ 0 \cr 1/2 \cr 0 \cr 1/6 \cr 1/3 } \right]$$

在 Inflation 之前，向量$A$ 就是一个正常的概率向量。为了令其具有更明显的区分度，对其进行 Inflation 强化。

假设$r$的取值为2，$A^2$如下：

$$A^2 = \left[ \matrix{ 0 \cr 1/4 \cr 0 \cr 1/36 \cr 1/9 } \right]$$

对该向量进行标准化，保证$\sum\limits_{i=1}^n A_i = 1$。

$$\Gamma_rA = \left[ \matrix{ 0 \cr 9/14 \cr 0 \cr 1/14 \cr 4/14 } \right]$$

可以看出，进过一次变换后，区分度进一步的增加，这就为之后的聚类提供了保证。在这里要注明的是Inflation 的参数$r$会影响聚簇的粒度，这个在之后会有说明。

MCL Algorithm

在MCL中， Expansion 和 Inflation 将不断的交替进行，Expansion 使得不同的区域之间的联系加强，而 Inflation 则不断的分化各点之间的联系。经过多次迭代，将渐渐出现聚集现象，以此便达到了聚类的效果。

MCL的算法流程具体如下：

1. 输入：一个非全连通图，Expansion 时的参数$e$和 Inflation 的参数$r$。

$$e = 2, r = 2$$

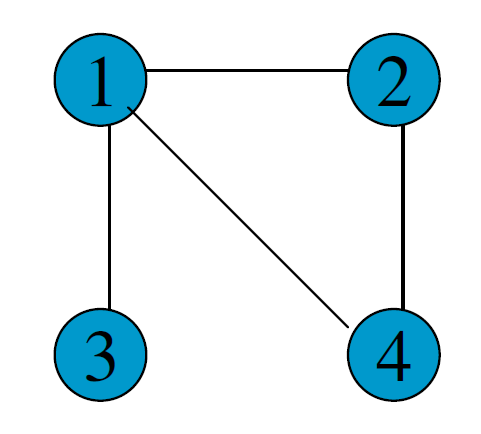
2. 建立邻接矩阵

   $$edge = \left[ \matrix{ 0 & 1 & 1 & 1 \cr 1 & 0 & 0 & 1 \cr 1 & 0 & 0 & 0 \cr 1 & 1 & 0 & 0 } \right]$$

3. 添加自环

   $$edge' = \left[ \matrix{ 1 & 1 & 1 & 1 \cr 1 & 1 & 0 & 1 \cr 1 & 0 & 1 & 0 \cr 1 & 1 & 0 & 1 } \right]$$

   ​

4. 标准化概率矩阵

   $$P_0 = \left[ \matrix{ 1/4 & 1/3 & 1/2 & 1/3 \cr 1/4 & 1/3 & 0 & 1/3 \cr 1/4 & 0 & 1/2 & 0 \cr 1/4 & 1/3 & 0 & 1/3 } \right]$$

5. Expansion操作，每次对矩阵进行$e$次幂方

   $$P_1 = P_0P_0 = \left[ \matrix{ .35 & .31 & .38 & .31 \cr .23 & .31 & .13 & .31 \cr .19 & .08 & .38 & .08 \cr .23 & .31 & .13 & .31 } \right]$$

6. Inflation操作，每次对矩阵内元素进行r次幂方，再进行标准化

   $$P_1' = \left[ \matrix{ .13 & .09 & .14 & .09 \cr .05 & .09 & .02 & .09 \cr .04 & .01 & .14 & .01 \cr .05 & .09 & .02 & .09 } \right] \\ \Gamma_rP_1 = \left[ \matrix{ .47 & .33 & .45 & .33 \cr .20 & .33 & .05 & .33 \cr .13 & .02 & .45 & .02 \cr .20 & .33 & .05 & .33 } \right]$$

7. 重复步骤5和6，直到达到稳定

8. 将结果矩阵转化为聚簇

MCL Algorithm Convergence

在作者的论文中，并没有证明MCL算法的收敛性。但是，在实验过程中，总是能够达到最终的收敛状态。下图是一个达到收敛的例子：

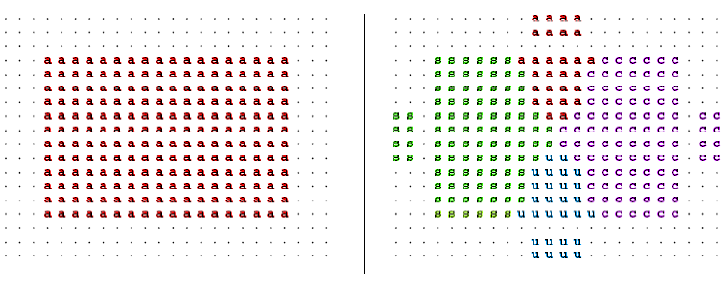
为了方便区分不同聚簇，我们将图上的点分为两类：Attractor 和 Vertex 。Attractor 代表了那些有着主导地位的点，这些点吸引着其它的点，将它们牢牢的聚集在周围；Vertex 则表示那些被吸引的点，它们没有主导地位，被 Attractor 所吸引着。其中，Attractor 所在的行必须至少有一个正值，聚集着它所在行中所有正值的点。可以看出，在这个例子中，总共有三个聚簇：{1，6，7，10}，{2，3，5}，{4，8，9，11，12}。

当然，在MCL中也会存在着重叠的聚簇。如下图，当且仅当簇与簇是同构的时才出现一个点被多个聚簇所吸引。

Inflation Parameter

在之前有提到过Inflation 参数会对聚簇产生影响。一般的，随着$r$的增大，其粒度将减小。

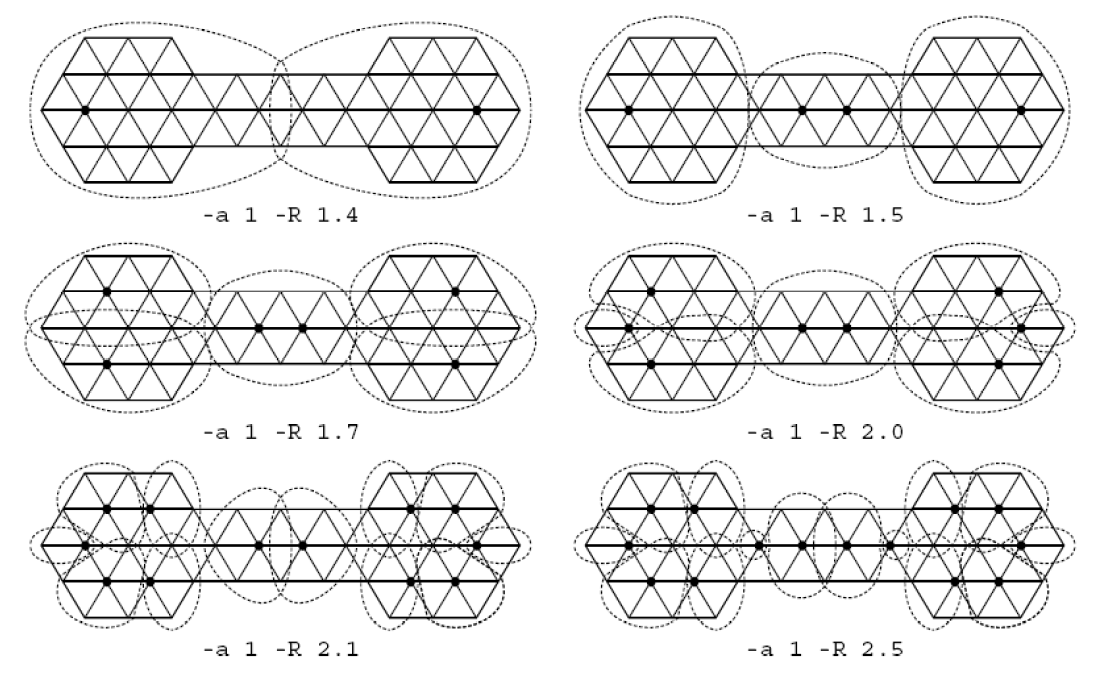
从上图中还可以看出，聚簇的多少和$e$有着很大的关系，在大直径的图中就更为明显了。因为偏远地区的点和簇群中心的联系越来越少，便很可能出现“挖墙脚”的可能，以及簇群内部分化问题。

Analysis of MCL

MCL有着较为优良的性能，总的来说，它的优缺点如下：

• 随着图大小的扩张，MCL有着良好的刻度

• 可以在有权或无权的图上运行

• 最后的聚类结果令人满意

• 可以较好的处理噪声数据

• 不需要人为规定簇群数量，而是可以根据参数自行确定

• 不能发现发生重叠的点

• 不适合在大图上使用（它的算法复杂度是$O(N^3)$）

以上是我对MCL的一些总结看法，欢迎大家来和我交流讨论。