AI贪吃蛇前瞻——基于Dijkstra算法的最短路径问题

    在贪吃蛇流程结构优化之后，我又不满足于亲自操刀控制这条蠢蠢的蛇，干脆就让它升级成AI，我来看程序自己玩，哈哈。

 一、Dijkstra算法原理

作为一种广为人知的单源最短路径算法，Dijkstra用于求解带权有向图的单源最短路径的问题。所谓单源，就是一个源头，也即一个起点。该算法的本质就是一个广度优先搜索，由中心向外层层层拓展，直到遇到终点或者遍历结束。该算法在搜索的过程中需要两个表S及Q，S用来存储已扫描过的节点，Q存储剩下的节点。起点s距离dist[s] = 0;其余点的值为无穷大（具体实现时，表示为某一不可能达到的数字即可）。开始时，从Q中选择一点u，放入S，以u为当前点，修改u周围点的距离。重复上述步骤，直到Q为空。

 

二、Dijkstra算法在AI贪吃蛇问题中的变化

2.1 地图的表示方法

    与平时见到的各种连通图问题不同，贪吃蛇游戏中的地图可以看成是标准的矩形，也即，一个二维数组，图中各个相邻节点的权值为1。因此，我们可以用一个边长*边长的二维数组作为算法的主体数据结构，讲地图有关的数据都集成在数组里。既然选择了二维数组，就要考虑数组元素类型的问题，即我们的数组应该存储哪些信息。作为主要的数据结构，我们希望我们的数组能存储自身的坐标，起点到自身的最短路径，因此我们可以定义这样的一个结构体：

  1. typedef struct loca{  
  2.     int x;  
  3.     int y;  
  4. }Local;  
  5.     
  6. typedef struct unit{  
  7.     int value;  
  8.     Local local;  
  9. }Unit;  

 

    又因为我们需要得到最短路径以求得贪吃蛇下一步的方向，所以在结构体里加一个指针，指向前一个节点的位置。

  1. typedef struct loca{  
  2.     int x;  
  3.     int y;  
  4. }Local;  
  5.     
  6. typedef struct unit{  
  7.     int value;  
  8.     Local local;  
  9.     struct unit *pre;  
  10. }Unit;  

 

假设地图为一个正方形，因此创建一个边长*边长大小的二维数组：

  1. #define N 5  
  2.     
  3. Unit mapUnit[N][N];  

 

2.2 队列——待处理节点的集合

    有了mapUnit之后，我们还需要一个数据结构来存储接下来需要处理的节点的信息。在此我选择了一个队列，由于C语言不提供标准的接口，就自己草草的写了一个。

  1. typedef struct queue{  
  2.     int head,tail;  
  3.     Local queue[N*N];  
  4. }Queue;  
  5.     
  6. Queue que;  

 

使用了一个定长的数组来作为队列结构，所以为了应对所有的结果，将其长度设为N*N。也正因为是定长数组，队列的进队与出队只需操作表示下标值的head与tail即可。这样虽然不节约空间，但胜在实现方便。

  1. void push(int x,int y)  
  2. {  
  3.     que.tail++;  
  4.     que.queue[que.tail].x = x;  
  5.     que.queue[que.tail].y = y;  
  6. }  
  7.     
  8. void pop()  
  9. {  
  10.     que.head++;  
  11. }  

 

由于push操作有一个自增操作，所以在初始化时需要将tail设为-1，这样在push第一个节点时可保证head与tail指向同一个位置。

 

2.3 console坐标——地图的初始化

    在我的贪吃蛇链表实现中，前端展示时通过后台的计算逻辑+Pos函数来实现的，也就是现在后台计算结果，再推动前台的变化。因此Pos()，也就是使光标跳转到控制台某位置的函数就尤为重要，这也直接影响了整个项目各元素的坐标表示方法。

    简单来说就是console的坐标表示类似于坐标轴中第四象限的表示方法，当然元素都为正值。

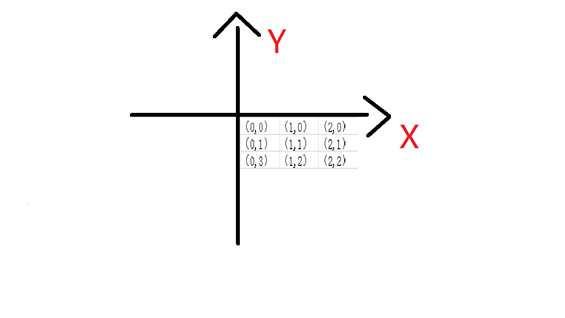
所以对于一个N*N的数组，我们可以这样初始化：

  1. void InitializeMapUnit()  
  2. {  
  3.     que.head = 0;  
  4.     que.tail = -1;  
  5.     
  6.     for(int i = 0;i<N;i++)  
  7.         for(int j = 0;j<N;j++)  
  8.         {  
  9.             mapUnit[i][j].local.x = i;  
  10.             mapUnit[i][j].local.y = j;  
  11.             mapUnit[i][j].pre = NULL;  
  12.             mapUnit[i][j].value = N*N;   
  13.         }  
  14. }  

 

将队列的初始化放在这个函数里实属无奈，这两行语句，又不能在初始化时赋值，又不能在函数体外赋值，放main函数嫌它乱，单独一个函数嫌它慢….就放在地图初始化里了…

 

三、计算，BFS！

3.1 设置起点

    基础的结构与初始化完成后，就需要开始计算了。在此之前，我们需要一个坐标，来作为路径问题的出发点。

  1. void setOrigin(int x,int y)  
  2. {  
  3.     mapUnit[x][y].value = 0;  
  4.     push(x,y);  
  5. }  

 

将地图上该点位置的值设为0后，将其压入队列中。在第一轮的BFS中，它四周的点，将成为第二轮计算的原点。

 

3.2 BFS框架

    在该地图的BFS中，我们将依托队列各个元素，来处理它们的邻接节点。两个循环，可以揭示大体的框架：

  1. void bfs(int end_x,int end_y)  
  2. {  
  3.     //当前需要处理的节点   
  4.     for(int i = head;i<=tail;i++)  
  5.     {  
  6.         //  四个方向   
  7.         for(int j = 0;j<4;j++)  
  8.         {  
  9.             // 新节点   
  10.             if(mapUnit[new_x][new_y].value == N*N)  
  11.             {  
  12.                 //设置属性   
  13.             }  
  14.             //  处理过的节点，取小值  
  15.             else       
  16.             {  
  17.                 //属性更改Or不变   
  18.             }  
  19.         }  
  20.     }  
  21.     //下一轮   
  22.     bfs();  
  23. }  

 

3.3 变化的队列

    BFS的主体循环依赖于队列的head与tail，但是对新节点的push操作改变了tail的值，所以我们需要在循环开始前将此时（上一轮BFS的结果）的队列状态保存下来，避免队列变化对BFS的影响。

  1. int head = que.head;  
  2. int tail = que.tail;  
  3. //当前队列  
  4. for(int i = head;i<=tail;i++)  
  5. {  
  6.     // TODO...   
  7. }   

 

3.4 节点的坐标

    在原来写的BFS中，要获取一个节点的下标需要将一个结构体层层剥开，数组的下标是一个结构体某元素的某元素，绕来绕去，可读性早已被献祭了。

所以这次我吸取了教训，在内循环，也就是处理周围节点时，将其坐标先存储在变量中，用来确保程序的可读性。

  1. for(int i = head;i<=tail;i++)  
  2. {  
  3.         int base_x = que.queue[i].x;  
  4.         int base_y = que.queue[i].y;  
  5.             
  6.         //  四个方向   
  7.         for(int j = 0;j<4;j++)  
  8.         {  
  9.             int new_x = base_x + direct[j][0];  
  10.             int new_y = base_y + direct[j][1];  
  11.                 
  12.             // TODO...   
  13.         }   
  14. }  

 

所以我们可以构建出这样一个移动的二维数组：

  1. //          方向， 上       下       左   右   
  2. int direct[4][2] = {{0,-1},{0,1},{-1,0},{1,0}};  

 

3.4.1 数组越界的处理

    在得到了待处理节点的坐标后，需要对其进行判断，确保它在数组内部。

  1. if(stepRight(new_x,new_y) == false)  
  2.     continue;  

 

函数细节如下：

  1. bool stepRight(int x,int y)  
  2. {  
  3.     if(x >= N || y >= N ||  
  4.         x < 0 || y < 0)  
  5.         return false;  
  6.     return true;  
  7. }  

 

 

3.5 新节点的处理

    终于到了访问邻接坐标的时候。一个节点四周的节点，有可能没有被访问过，也可能以及被访问过。我们在初始化时就将所有节点的值设为了一个MAX，通过对值得判断，可以推断出其是否为新节点。

  1. if(mapUnit[new_x][new_y].value == N*N)  
  2. {  
  3.     // ...  
  4. }  
  5. else    //取小值   
  6. {  
  7.     // ...  
  8. }  

3.5.1 未处理节点的处理

    对于未处理的节点，对其的操作有两部。一是初始化，值的初始化与指针的初始化。由于两点间的距离为1，所以该节点的值为前一个节点的值+1，当然，他的pre指针也指向前一个节点。

  1. mapUnit[new_x][new_y].value = mapUnit[base_x][base_y].value +1;  
  2. mapUnit[new_x][new_y].pre = &mapUnit[base_x][base_y];  
  3. push(new_x,new_y);  

 

3.5.2 已处理节点的处理

    对于已处理过的节点，需要先将其做一个判断，即寻找最短路径，将其自身的value与前一节点value+1比较，再处理。

  1. mapUnit[new_x][new_y].value = MIN(mapUnit[new_x][new_y].value,mapUnit[base_x][base_y].value +1);  
  2. if(mapUnit[new_x][new_y].value != mapUnit[new_x][new_y].value)  
  3. mapUnit[new_x][new_y].pre = &mapUnit[base_x][base_y];  

 

3.6 队列的刷新

    在处理完一层节点后，新的节点导致了队列中tail的增加，但是head并没有减少，所以在新一轮BFS前，需要将队列的head移动到真正的头部去。

  1. for(int i = head;i<=tail;i++)  
  2.     pop();  

 

在这儿也需要当前BFS轮数前的队列数据。

 

3.7 最短路径

    在地图的遍历完成之后，我们就可以任取一点，得到起点到该点的最短路径。

  1. void getStep(int x,int y)  
  2. {  
  3.     Unit *scan = &mapUnit[x][y];  
  4.     if(scan->pre!= NULL)  
  5.     {  
  6.         int x = scan->local.x;  
  7.         int y = scan->local.y;  
  8.         scan = scan->pre;  
  9.         getStep(scan->local.x,scan->local.y);  
  10.         printf(" -> ");  
  11.     }  
  12.     printf("(%d,%d)",x,y);  
  13. }  

 

四、此路不通——障碍的引入

    在贪吃蛇中，由于蛇身长度的存在，以及蛇头咬到自身就结束的特例，我们需要在算法中加入障碍的元素。

    对于这个新加入的元素，我们设置一个坐标结构体的数组，来存储所有的障碍。

  1. #define WALL_CNT 3   
  2. Local Wall[WALL_CNT];  

 

    用一个函数来设置障碍：

  1. void setWall(void)  
  2. {  
  3.     Wall[0].x = 1;  
  4.     Wall[0].y = 1;  
  5.         
  6.     Wall[1].x = 1;  
  7.     Wall[1].y = 2;  
  8.         
  9.     Wall[2].x = 2;  
  10.     Wall[2].y = 1;  
  11. }  

 

    由于这个项目里数据用于模块测试的随机性，所以手动设置每一个坐标。在之后的贪吃蛇AI中，将接受一个数组——蛇身，来自动完成赋值。

    如果将障碍与地图边界等同来看，就能将障碍的判断整合进stepRight()函数。

  1. bool stepRight(int x,int y)  
  2. {  
  3. //  out of map   
  4.     if(x >= N || y >= N ||  
  5.         x < 0 || y < 0)  
  6.         return false;  
  7. //  wall  
  8.     for(int i = 0;i<WALL_CNT;i++)  
  9.         if(Wall[i].x == x && Wall[i].y == y)  
  10.             return false;  
  11.         
  12.     return true;  
  13. }  

 

五、简单版本的测试

    完成了上诉的模块后，项目就可以无BUG但是低效的跑了。我们来试一试，在一个5*5的地图中，起点在中间，为（2，2），终点在起点的上上方，为（2，0），设置三面围墙，分别是（1，1），（2，1），（3，1）。如下：

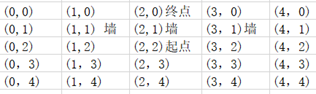
    看看效果。

    图中二维数组打印了各个坐标点的value，即该点到起点的最短路径。25为墙，0为起点。可以看到到终点需要六步，路径是先往左，再往上，左后向右到终点。

    任务完成，看似不错。把终点换近一些看看，就（1，4）吧。

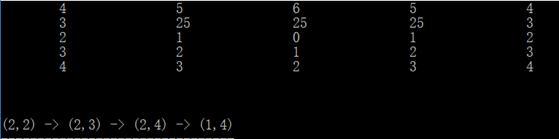
    喔，问题出来了。我取一个非常近的点，但是整张图都被遍历了，效率太低了，要改进。

    还有一个问题，如果将起点周围四个点都设置为墙，结果应该是无法得到其余点的最短路径，但现阶段的结果还不尽如人意：

 

六、优化

6.1 遍历的半途结束

    在BFS中，如果找到了终点，那就可以退出遍历，直接输出结果。不过这样的一个递归树，要随时终止可不容易。我一开始想到了"万恶之源"goto，不过goto不能跨函数跳转，随后又想到了非本地跳转setjmp与longjmp。

"与刺激的abort()和exit()相比,goto语句看起来是处理异常的更可行方案。不幸的是，goto是本地的：它只能跳到所在函数内部的标号上，而不能将控制权转移到所在程序的任意地点（当然，除非你的所有代码都在main体中）。

为了解决这个限制，C函数库提供了setjmp()和longjmp()函数，它们分别承担非局部标号和goto作用。头文件<setjmp.h>申明了这些函数及同时所需的jmp_buf数据类型。"

 

    有了这随时能走的"闪现"功能，跳出复杂嵌套函数还是事儿嘛？

  1. #include <setjmp.h>  
  2. jmp_buf jump_buffer;  
  3.     
  4. int main (void)  
  5. {  
  6.     //...  
  7.     if(setjmp(jump_buffer) == 0)  
  8.         bfs(finishing_x,finishing_y);  
  9.     //...  
  10. }  

    由于跳转需要判断当前节点是否为终点，而终点又是一个局部变量，所以需要改变bfs函数，使其携带终点参数。

    再在处理完一个节点后，判断其是否为终点，是则退出。

  11. for(int i = head;i<=tail;i++)  
  12. {  
  13.     //...  
  14.     //  四个方向   
  15.     for(int j = 0;j<4;j++)  
  16.     {  
  17.         //...  
  18.         if(mapUnit[new_x][new_y].value == N*N)  
  19.         {  
  20.             //...  
  21.         }  
  22.         else    //取小值   
  23.         {  
  24.             //...  
  25.         }  
  26.         if(new_x == end_x && new_y == end_y)  
  27.         {  
  28.             longjmp(jump_buffer, 1);  
  29.         }  
  30.     }  
  31. }  

 

6.2 无最短路径时的处理

    在判断某一点的路径时，可先判断其是否存在最短路径，存在则输出，否则给出提示信息。

  1. void getStepNext(int x,int y)  
  2. {  
  3.     Unit *scan = &mapUnit[x][y];  
  4.     if(scan->pre!= NULL)  
  5.     {  
  6.         int x = scan->local.x;  
  7.         int y = scan->local.y;  
  8.         scan = scan->pre;  
  9.         getStepNext(scan->local.x,scan->local.y);  
  10.         printf(" -> ");  
  11.     }  
  12.     printf("(%d,%d)",x,y);  
  13. }  
  14.     
  15. void getStep(int x,int y,int orgin_x,int orgin_y)  
  16. {  
  17.     Unit *scan = &mapUnit[x][y];  
  18.     Pos(0,10);  
  19.         
  20.     if(scan->pre == NULL)  
  21.     {  
  22.         printf("NO Path To Point (%d,%d) From Point (%d,%d)!\n",x,y,orgin_x,orgin_y);  
  23.     }  
  24.     else  
  25.     {  
  26.         getStepNext(x,y);  
  27.     }  
  28. }  

 

七、优化后效果

 

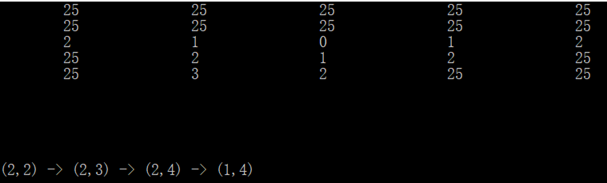
八、写在后面

    算法大体上完成了，将其改为贪吃蛇AI也只需做少量修改。尽量抽个时间把AI写完，不过可能需要一段时间。

    在最短路径的解法上，Dijkstra算法并不是最理想的解法。盲目搜索的效率很低。考虑到地图上存在着两点间距离等信息，可以使用一种启发式搜索算法，如BFS(Best-First Search)，以及大名鼎鼎的A*算法。在中文互联网我能找到的有关于A*算法的资料不多，将来得花些时间好好研究下。

    源码地址：https://github.com/MagicXyxxx/Algorithms    

 

posted on 2019-02-28 23:03  Magic激流  阅读(2045)  评论(0)  编辑  收藏  举报

导航