海明码
海明码学习前提
学习海明码之前，我们要约定3个原则：
- 海明码只能检测出2位错，纠1位错(因此不要问如果3位错怎么办等幼稚问题)。
- 海明码默认进行偶校验(除非特殊说明使用奇校验)。
- 海明码是一串由0和1组成的序列(除01外没有其他的值，记住了！这是重点)
如果下面有任何无法理解的问题，反复看上面三个原则，下面再也不赘述。
前提：奇偶校验
奇校验：这串序列1的个数如果为偶数则在前面加个1，使1的个数变成奇数，否则加0。
偶校验：这串序列1的个数如果为奇数则在前面加个1，使1的个数变成偶数，否则加0。
例子：1111 奇校验就是 11111 偶校验就是 011111110 奇校验就是 01110 偶校验就是 11110
特性是检测一位错，无法纠错。
概述：海明码的构成
例如如下序列：1100
我们想要让其变成海明码只需如下操作
1.算出校验位数k
正常情况下我们需要如下此操作：
2^k >= k + 数据位数 + 1
这里等于3
2.确定校验位在海明码中的位置
这里按2^k次幂留出来，就像1，2，4，8，16，32。（如果问有5位等其他烦人的数据位怎么办后面我会说，先按4位数做）
| H7 | H6 | H5 | H4 | H3 | H2 | H1 |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 |
3.分组（重点，很多人蒙圈就在此）
我们需要确认H1,H2,H4这三个校验位都来校验哪些位置。
我们按这个规则进行分配。
将1,2,4（海明码下标为1,2,4）
的二进制码写出来，并且最高位补到3位(前面算的K数)
如下所示：
| 1 | 2 | 4 |
|---|---|---|
| 001 | 010 | 100 |
然后我们将0替换为*，作为通配表。
| 1 | 2 | 4 |
|---|---|---|
| **1 | *1* | 1** |
我们将1到7的二进制序列，列出来如下表
| 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|
| 111 | 110 | 101 | 100 | 011 | 010 | 001 |
！！！重点！！！！
我们将7->1依次与上面的通配表进行匹配
| 1 | 2 | 4 |
|---|---|---|
| **1 | *1* | 1** |
| 001（1） | 010（2） | 100（4） |
| 011（3） | 011（3） | 101（5） |
| 101（5） | 110（6） | 110（6） |
| 111（7） | 111（7） | 111（7） |
因此我们可以确定
H1 负责 1 3 5 7 位数的校验
H2 负责 2 3 6 7 位数的校验
H4 负责 4 5 6 7 位数的校验
4.求出校验位是0还是1
因为上面我们得出以下结论：
H1 负责 1 3 5 7 位数的校验
H2 负责 2 3 6 7 位数的校验
H4 负责 4 5 6 7 位数的校验
那 根据
| H7 | H6 | H5 | H4 | H3 | H2 | H1 |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | |||
| 这张表，我们根据偶校验很容易就求出以下结论： | ||||||
| H3,H5,H7 1的个数为奇数 因此H1=1 | ||||||
| H3,H6,H7 1的个数为偶数 因此H2=0 | ||||||
| H5,H6,H7 1的个数为偶数 因此H4=0 | ||||||
| 至此我们得出了完整的汉明码 |
| H7 | H6 | H5 | H4 | H3 | H2 | H1 |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
5.查错
查错比较简单，如果以下三组
既
H1,H3,H5,H7
或者
H2,H3,H6,H7
或者
H4,H5,H6,H7
偶校验出错，则出错。
比方说 如果 H1,H3,H5,H7由1100 变成了 1110 （1的个数为偶数）就是出错了
这里该不赘述
6.纠错
首先我们先理解以下为什么海明码能纠错。
首先我们先画个圆。然后按如下形式做交叉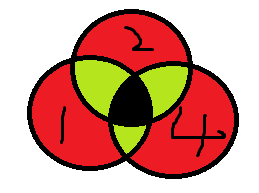
在每个相邻部位，我们做相加处理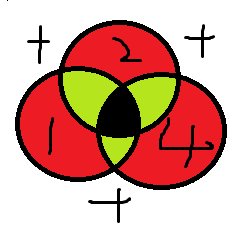
变成了如下形式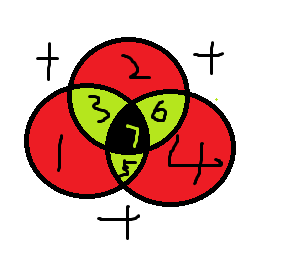
当我们如果发现偶校验出错，
比方说在 1 3 7 5 这个区域出错。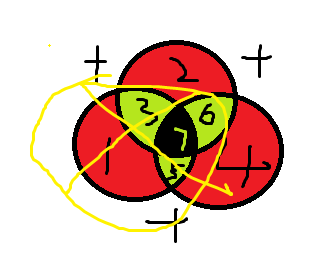
如果这个位置出错了，那么一定是 1 3 7 5 这四个位置中的一个位置出错(如果俩位出错则无法纠错，这个点一定要记住)
如果此时其他的俩个组 即：2，3，6，7 和 4，5，6，7偶校验都通过了的话。
也就证明只可能是1出错
所以我们可以将 1 的位数 做修改。如果是0变为1，如果是1变为。来达到纠错的目的。
但是如果2，3，5，7这个位置也出错了，4，5，6，7这个位置没有出错。
我们很容易就推导出，是 3 这个位置出错了。
我们就可以修改3的值，如果是0变为1或者如果是1变为0.
在此时我们会发现一个巧妙的规则！
当我们把1，3，5，7 设为P1,
2,3,6,7设为P2
4,5,6,7设为P3时
当如果哪组校验失败就为1
| P3 | P2 | P1 | 出错(第几)位数 |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 2 |
| 0 | 1 | 1 | 3 |
| 1 | 0 | 0 | 4 |
| 1 | 0 | 1 | 5 |
| 1 | 1 | 0 | 6 |
| 1 | 1 | 1 | 7 |
刚好是对应的二进制编码。就是这么绝。
其实学完海明码之后，我真的觉得人家实在是太聪明了。
5位数数据
至此，其实如果认真看上面的部分，大家已经可以理解海明码是如何实现的了。
但是我还是再带大家写一次。这种5位数的。关键在于如何分组！！！！！
比方说10001
先求出校验位数：
2 ^ k > = k + 5 + 1
则 k = 4
画出表格
将1，2，4，8位置空出来，再将数据位填进去
| H9 | H8 | H7 | H6 | H5 | H4 | H3 | H2 | H1 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 |
分组(*为通配符)
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1*** | *1** | **1* | ***1 |
| 8,9 | 4,5,6,7 | 2,3,6,7 | 1,3,5,7,9 |
偶校验每个分组得出结果
| H9 | H8 | H7 | H6 | H5 | H4 | H3 | H2 | H1 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
总结
如果还有人不懂，请仔仔细细跟着我走一遍。本人保证此思路是绝对正确的。
