谜题：在25匹马中找到最快的3匹马

谜题：

　　有 25 匹马，你需要找出最快的 3 匹马，现有最多 5 个赛道给马进行比赛，以便分出出它们之间的相对速度。在任何时候，你都无法找到得到赛马的实际速度（没有计时器等工具）。找出获得前三名的马需要进行多少场比赛。 

解答：

　　首先，我们将马匹分为 5 组，并在赛道上对每组进行比赛。

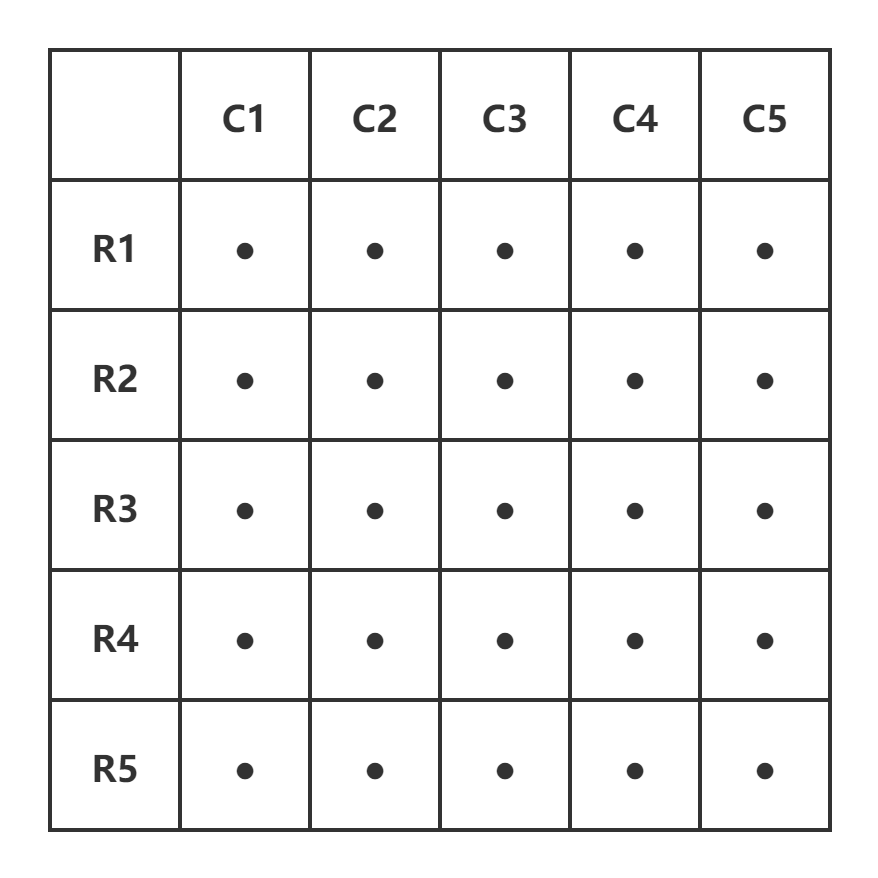
　　在上面的表格中，每一行代表 5 匹马的一场比赛。方便起见，利用坐标（Row，Col）为每一匹马命名。因此，第一场比赛（第 1 行）在（1，1）、（1，2）、（1，3）、（1，4）和（1，5）这 5 匹马之间进行比赛。第二场（第 2 行）在（2，1）、（2，2）等马匹之间进行比赛。

　　假设每行的第 5 匹马赢得了比赛（（1，5）赢得第一场比赛，（2，5）赢得了第二场比赛，以此类推），每行的第 4 匹马赢得了第 2 名（和前面冠军的方式类推），每行的第 3 匹马赢得了第 3 名。当然这些假设是其中一个可能，方便理解。

 

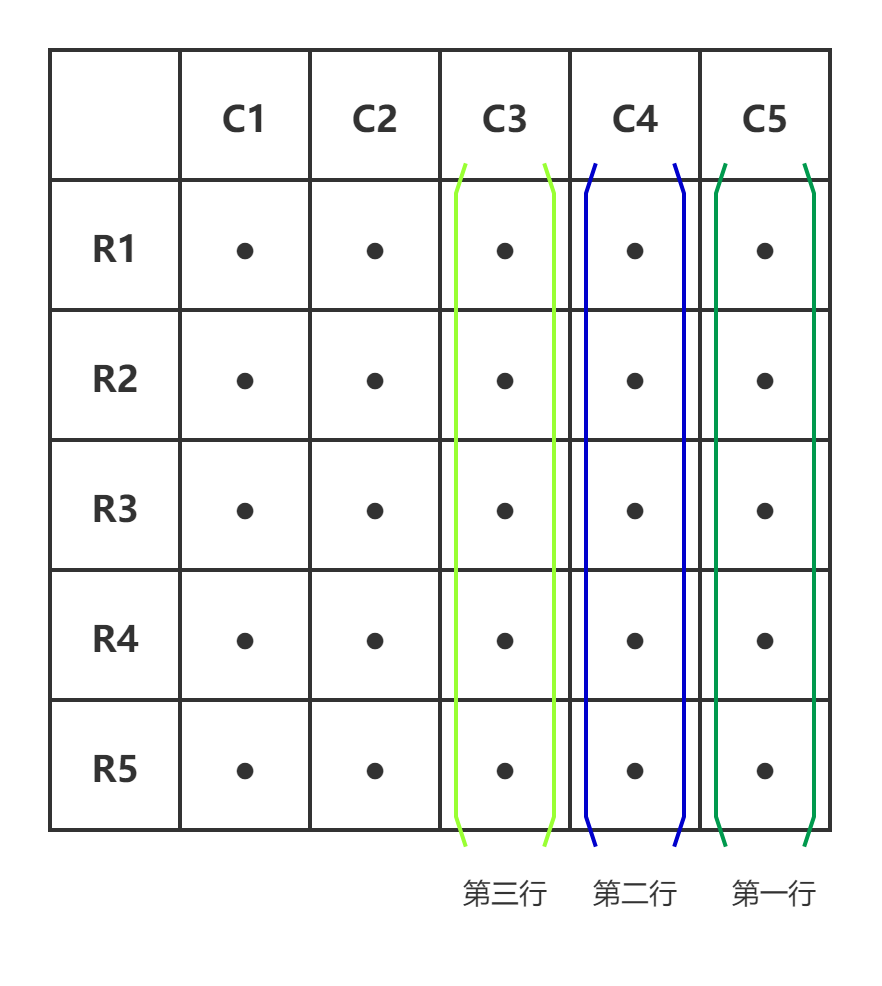
　　接下来，让每行（组）冠军（1，5）、（2，5）等 5 匹马进行对决。假设（1，5）位居第一，（2，5）位居第二，（3，5）位居第三。

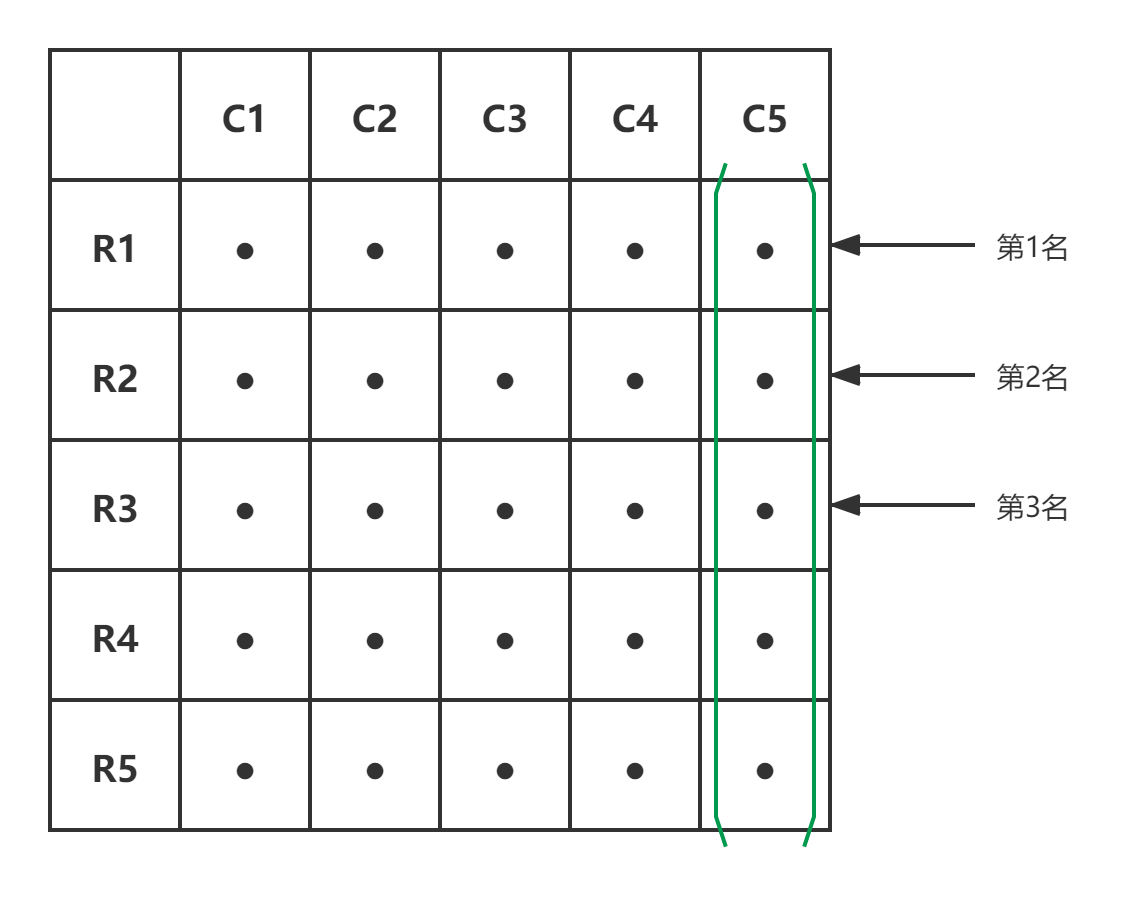
　　这场比赛在团体中最快的马是（1，5）。整体排名第 2 的马可能是是（2，5）或（1，4），在整个组中排在第三的马是可以是（3，5）、（2，4）或（1，3）。因此将对 5 匹马进行比赛。

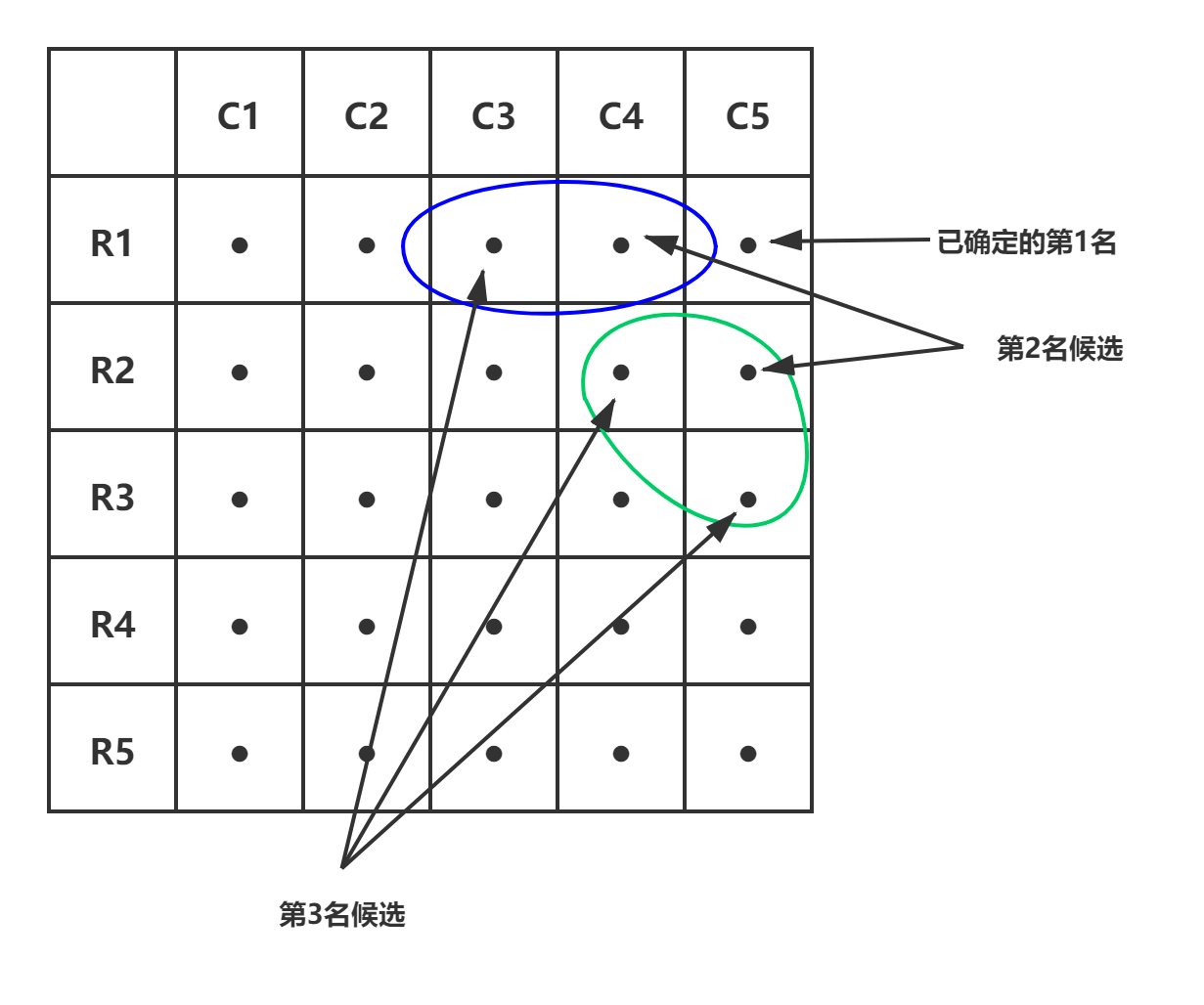
　　因此，最快的马是（1，5）。在最后一场比赛中排名第 2 和第 3 的马分别是整个组中第 2 和第 3 的马。这样，确定整个组中最快的第 1、第 2 和第 3 匹马所需最少比赛数目为 7。