算法:Z字型(Zigzag)编排
问题:给定 n 行和 m 列的二维数组矩阵。如图所示,以 ZIG-ZAG 方式打印此矩阵。
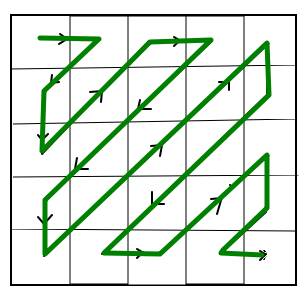
从对称的角度来看,通过反复施加滑行反射可以从简单的图案如线段产生规则的之字形。
主要思想:算法从(0, 0)位置开始水平向右遍历,当到达(0, 1)时沿着反对角线方向左下遍历(利用一个变量控制左下右上方向),内层循环一直遍历到碰到边缘时row++,方向改为右上,沿着反对角线碰到矩阵上边缘时col++,方向变为左下遍历,知道上半部分(包括反对角线遍历完);遍历完半个矩阵(可能是子方矩阵)后,根据当前 row 索引和 col 索引所在位置来判断延伸方向,若碰到边缘,则对应行列索引数加一,没碰到边缘,则按内层循环的思路延伸,然后相同的思路遍历完矩阵剩下部分。
算法的时间复杂度为 O(n*m),其中 n, m 为输入矩阵的行数和列数,空间复杂度为 O(1)。
1 package algorithm; 2 3 public class ZArrangement { 4 5
6 7 /** 8 * Z字型编排打印矩阵 9 * 10 * @param arr 矩阵 11 * @param n 指定子矩阵的行 12 * @param m 指定子矩阵的列 13 */ 14 private static void zigzagMatrix(int[][] arr, int n, int m) { 15 int row = 0, col = 0; 16 17 /* 行增长变量,控制↙和↗的布尔型变量*/ 18 boolean row_inc = false; 19 20 // 打印上半(包括反对角线)Z字形图案的矩阵 21 int mn = Math.min(m, n); 22 for (int len = 1; len <= mn; ++len) { 23 for (int i = 0; i < len; ++i) { 24 System.out.print(arr[row][col] + " "); 25 26 if (i + 1 == len) { 27 break; 28 } 29 30 // 如果row_increment值为true,增加行并减少列, 否则递减行并递增列 31 if (row_inc) { 32 // ↙ 33 ++row; 34 --col; 35 } else { 36 // ↗ 37 --row; 38 ++col; 39 } 40 } 41 42 if (len == mn) { 43 break; 44 } 45 46 // 根据最后的增量更新行或列的值 47 if (row_inc) { 48 ++row; 49 row_inc = false; 50 } else { 51 ++col; 52 row_inc = true; 53 } 54 } 55 56 57 // 更新row和col变量的索引 58 if (row == 0) { 59 if (col == m-1) 60 ++row; 61 else 62 ++col; 63 row_inc = true; 64 } else { 65 if (row == n-1) 66 ++col; 67 else 68 ++row; 69 row_inc = false; 70 } 71 72 // 打印剩下的Z字型图案矩阵 73 int MAX = Math.max(m, n) - 1; 74 for (int len, diag = MAX; diag > 0; --diag) { 75 if (diag > mn) 76 len = mn; 77 else 78 len = diag; 79 80 for (int i = 0; i < len; ++i) { 81 System.out.print(arr[row][col] + " "); 82 83 if (i + 1 == len) 84 break; 85 86 // 根据最后的增量更新行或列的值 87 if (row_inc) { 88 ++row; 89 --col; 90 } else { 91 ++col; 92 --row; 93 } 94 } 95 96 // 更新row和col变量的索引 97 if (row == 0 || col == m-1) { 98 if (col == m-1) 99 ++row; 100 else 101 ++col; 102 row_inc = true; 103 } 104 105 else if (col == 0 || row == n-1) { 106 if (row == n-1) 107 ++col; 108 else 109 ++row; 110 row_inc = false; 111 } 112 } 113 } 114 115 public static void main(String[] args) { 116 int[][] matrix = { 117 {1, 2, 3}, 118 {4, 5, 6}, 119 {7, 8, 9} 120 }; 121 zigzagMatrix(matrix, 3, 3); 122 } 123 }




