Huffman算法
一、Huffman算法介绍
霍夫曼编码(英语:Huffman Coding),又译为哈夫曼编码、赫夫曼编码,是一种用于无损数据压缩的熵编码(权编码)算法。在计算机数据处理中,霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现几率的方法得到的,出现几率高的字母使用较短的编码,反之出现几率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
霍夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。
前缀代码表示以一种方式分配代码(位序列),以使分配给一个字符的代码不是分配给任何其他字符的代码的前缀。这就是霍夫曼编码如何确保在解码生成的比特流时没有歧义的地方。
让我们通过一个反例来了解前缀代码。假设有四个字符a,b,c和d,它们对应的可变长度代码分别为00、01、0和1。由于分配给c的代码是分配给a和b的代码的前缀,因此这种编码会产生歧义。如果压缩的比特流是0001,则解压缩的输出可以是“ cccd”或“ ccb”或“ acd”或“ ab”。
霍夫曼编码主要包括两个主要部分:
1)根据输入字符构建霍夫曼树。
2)遍历霍夫曼树并将代码分配给字符。
二、构建霍夫曼树的步骤
输入是唯一字符及其出现频率的数组,输出是霍夫曼树。
1. 为每个唯一字符创建一个叶节点,并为所有叶节点建立一个最小堆(Min Heap用作优先级队列。frequency字段的值用于比较最小堆中的两个节点。最初,把最不频繁的字符作为根)
2. 从最小堆中提取频率最小的两个节点。
3. 创建一个频率等于两个节点频率之和的新内部节点。使第一个提取的节点为其左子节点,另一个提取的节点为其右子节点。将此节点添加到最小堆中。
4. 重复步骤2和3,直到堆仅包含一个节点。其余节点是根节点,树已完成。
一个例子:
| 字符 | A | B | C | D | E |
| 频率 | 1 | 7 | 6 | 5 | 2 |
步骤1:构建一个包含5个节点的最小堆,其中每个节点代表具有单个节点的树的根。
步骤2:从最小堆中提取两个最小频率节点。添加一个频率为1 + 2 = 3的新内部节点。
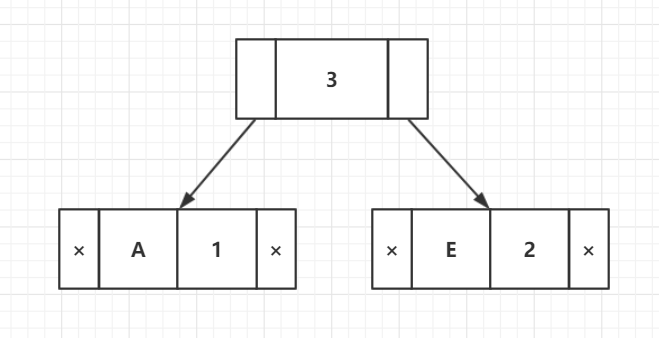
现在最小堆包含4个节点,其中3个节点是每个具有单个元素的结点,一个堆节点是具有3个元素。
| 字符 | 频率 |
| 内部节点 | 3 |
| D | 5 |
| C | 6 |
| B | 7 |
步骤3:从堆中提取两个最低频率节点。添加频率为12 + 13 = 25的新内部节点

现在最小堆包含3个节点,其中2个节点是每个具有单个元素的节点,两个堆节点是具有多个节点的子树。
| 字符 | 频率 |
| 内部节点 | 8 |
| C | 6 |
| B | 7 |
步骤4:提取两个最低频率节点。添加频率为6 + 7 = 13的新内部节点
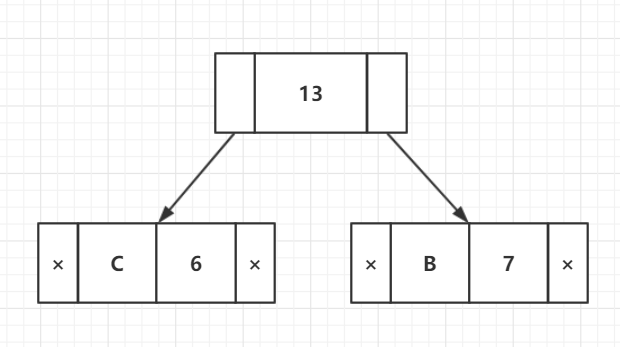
现在,最小堆包含2个节点。
| 字符 | 频率 |
| 内部节点 | 8 |
| 内部节点 | 13 |
步骤6:提取两个最低频率节点。添加频率为8 + 13 = 21的新内部节点
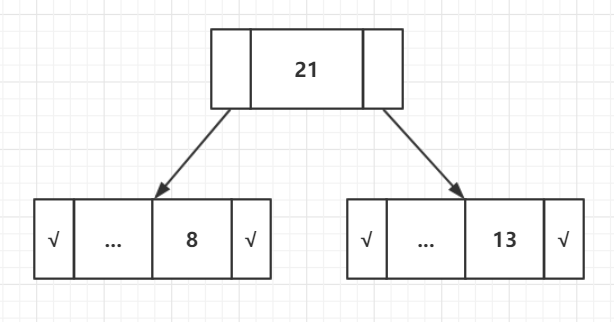
现在最小堆中只剩下一个节点,因此算法在此处停止。
从霍夫曼树打印代码的步骤:
遍历从根开始形成的树。维护一个辅助阵列。当移到左孩子时,将0写入数组。当移动到正确的孩子时,将1写入数组。遇到叶节点时打印阵列。
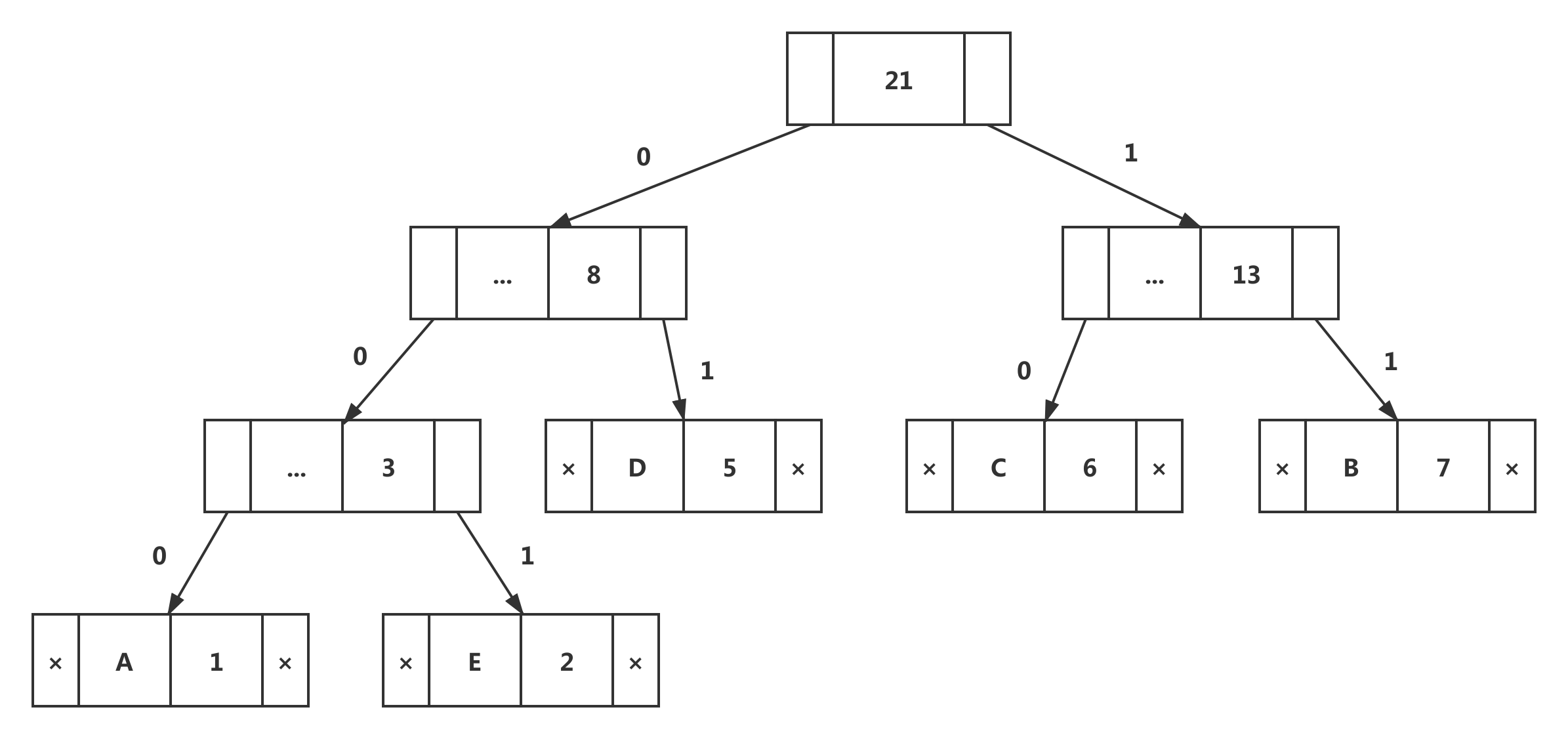
输出如下:
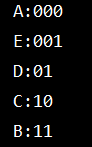
源代码:

1 package tree; 2 3 import java.util.Comparator; 4 import java.util.PriorityQueue; 5 6 /** 7 * 这是一个哈夫曼树 (Huffman Tree),用于无损数据压缩的熵编码算法 8 * 哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。 9 */ 10 public class HuffmanTree { 11 12 /** 13 * 通过树遍历的霍夫曼代码 14 * @param root 15 * @param s 16 */ 17 public static void printCode(HuffmanNode root, String s) { 18 /* 如果左右为空,那么这就是一个叶子结点 */ 19 if (root.left == null && root.right == null && Character.isLetter(root.c)) { 20 System.out.println(root.c + ":" + s); 21 return; 22 } 23 assert root.left != null; 24 printCode(root.left, s + "0"); 25 printCode(root.right, s + "1"); 26 } 27 28 public static void main(String[] args) { 29 30 int n = 5; // 字符数量 31 32 /* 下面那个例子的最后结果: 33 A:000 34 E:001 35 D:01 36 C:10 37 B:11 38 */ 39 char[] charArray = {'A', 'B', 'C', 'D', 'E'}; 40 int[] charfreq = {1, 7, 6, 5, 2}; 41 42 /* 创建优先级队列q,创建一个最低优先级队列(min-heap)。*/ 43 PriorityQueue<HuffmanNode> q = new PriorityQueue<>(n, new MyComparator()); 44 45 /* 为每个字符创建一个Huffman树的叶子结点,并 */ 46 for (int i = 0; i < n; i++) { 47 /* 创建一个Huffman节点对象,并将其添加到优先级队列。*/ 48 HuffmanNode hn = new HuffmanNode(); 49 50 hn.c = charArray[i]; 51 hn.data = charfreq[i]; 52 53 hn.left = null; 54 hn.right = null; 55 56 q.add(hn); 57 } 58 59 /* 创建一个Huffman根节点 */ 60 HuffmanNode root = null; 61 62 while (q.size() > 1) { 63 /* 提取第一个最小的。*/ 64 HuffmanNode x = q.peek(); 65 q.poll(); 66 67 /* 提取第二个最小的。*/ 68 HuffmanNode y = q.peek(); 69 q.poll(); 70 71 /* 新建一个新结点,将两个节点的频率之和分配给f节点 */ 72 HuffmanNode f = new HuffmanNode(); 73 f.data = x.data + y.data; 74 f.c = '-'; 75 76 f.left = x; 77 f.right = y; 78 79 root = f; 80 81 q.add(f); 82 } 83 84 printCode(root, ""); 85 } 86 } 87 88 /** 89 * 哈夫曼节点 90 */ 91 class HuffmanNode { 92 int data; 93 char c; 94 95 HuffmanNode left; 96 HuffmanNode right; 97 } 98 99 /** 100 * 用于比较哈夫曼节点值的大小 101 */ 102 class MyComparator implements Comparator<HuffmanNode> { 103 104 @Override 105 public int compare(HuffmanNode o1, HuffmanNode o2) { 106 return o1.data - o2.data; 107 } 108 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号