字符串与模式匹配算法(三):KMP算法
一、KMP算法介绍
KMP算法与前面的MP算法一脉相承,都是充分利用先前匹配的过程中已经得到的结果来避免频繁回溯。回顾一下MP算法,如下图的模式串偏移,当前模式字符串P的左端的p0与目标字符串T中tj位置对齐。从左向右逐个进行比较,发现 pi 处的字符a 与 tj+1 处字符b发生失配。同时也表明 P(p0,p1,...,pi-1) 与 T'(tj,tj+1,...,tj+i-1) 是完全匹配的,这一部分子串在图中用字母u标示出。由于发生失配,随即移动模式字符串并进行下一轮的比较。此时,很自然地希望移动之后的结果可以使得模式字符串P中的一个前缀v,可以匹配到子串u的某一部分后缀。所以MP算法引入一个mpNext数组,并用它来对P中最长前缀进行标记。然后根据PmpNext[i] = c 和 Ti+j = b 之间展开下一轮比较。
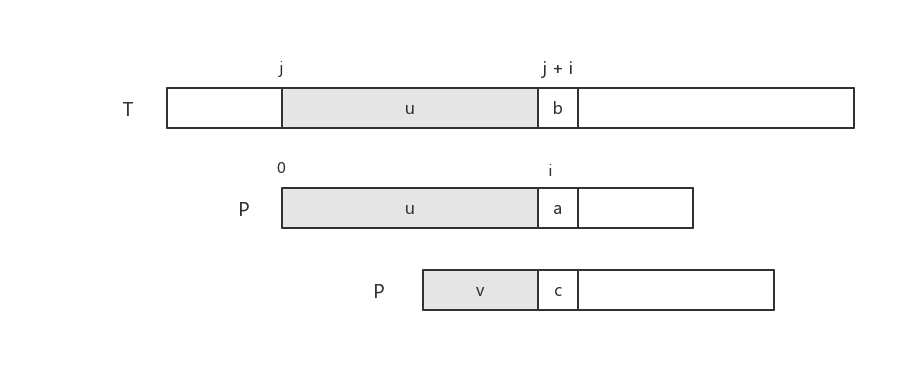
在MP算法的基础上再推进一步,继续前面的过程,当模式字符串P完成一次移动后,接下来马上要进行的工作是比较字符 b 和 c,为了避免随之而来的一次失配,在仅仅知道模式字符串P的情况下,保证一次移动后,紧随着前缀字符串v之后的那个字符c不等于原来失配的字符a(满足这个条件的最长前缀v是字符串u的加标边际)。KMP算法需要对mpNext表中符合要求的加标边际进行标识,符合要求指的是:① v可以匹配到u中某个后缀的最长前缀; ② 紧跟在v后面的字符c不同于紧跟在u后面的字符a。
二、kmpNext表的规则
在mpNext表生成的基础上,建立kmpNext表的规则分为4种情况,其中 1≤j≤m-1:
-
如果 mpNext[j] = 0 且 pj = p0,则令kmpNext[j] = -1;
-
如果 mpNext[j] = 0 且 pj ≠ p0,则令kmpNext[j] = 0;
-
如果 mpNext[j] ≠ 0 且 pj ≠ pmpNext[j],则令kmpNext[j] = mpNext[j];
-
如果 mpNext[j] ≠ 0 且 pj = pmpNext[j],则用mpNext[j]中的值替换原来mpNext[j]中的j值,直到情况转换为前面3种情况的一种,从而递归求解kmpNext[j]。
在 j =0 的位置同样是 -1,并令kmpNext[m] = mpNext[m],m是模式串P的长度。kmpNext[m]的值也是指示了后续进行匹配而需要将模式字符串移动的位数。
kmpNext表:
|
j |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
p(j) |
c |
a |
a |
t |
c |
a |
t |
|
|
mpNext[j] |
-1 |
0 |
0 |
0 |
0 |
1 |
2 |
0 |
|
kmpNext[j] |
-1 |
0 |
0 |
0 |
-1 |
0 |
2 |
0 |
三、代码
1 public void preKmp(char[] x, int m, int[] kmpNext) { 2 int i, j; 3 i = 0; 4 j = kmpNext[0] = -1; 5 while(i < m-1) { 6 while (j > -1 && x[i] != x[j]) 7 j = kmpNext[j]; 8 i++; 9 j++; 10 if (x[i] == x[j]) 11 kmpNext[i] = kmpNext[j]; 12 else 13 kmpNext[i] = j; 14 } 15 } 16 17 public void kmp(String p, String t) { 18 int m = p.length(); 19 int n = t.length(); 20 21 if (m > n) { 22 System.err.println("Unsuccessful match!"); 23 return; 24 } 25 26 char[] x = p.toCharArray(); 27 char[] y = t.toCharArray(); 28 29 int i = 0; 30 int j = 0; 31 int[] kmpNext = new int[m+1]; 32 preKmp(x, m, kmpNext); 33 34 while (j < n) { 35 while (i > -1 && x[i] != y[j]) 36 i = kmpNext[i]; 37 i++; 38 j++; 39 if (i >= m) { 40 System.out.println("Matching index found at: " + (j - i + 1)); 41 i = kmpNext[i]; 42 } 43 } 44 }



