字符串与模式匹配算法（二）：MP算法

一、MP算法介绍

　　MP 算法（Morris-Pratt算法）是一种快速串匹配算法，它是詹姆斯·莫里斯（James Morris）和沃恩·普莱特（Vaughan Pratt）在1970年提出的一种快速匹配算法，这个算法对 BF 算法的改进很大，主要体现在匹配失败时，目标指针不用回溯，而是利用已经得到的“部分匹配”结果，将模式向右“滑动”若干位置后继续比较，避免了频繁回溯，普遍提高了匹配的工作效率，因此又被称为不回溯的字符串搜索算法。

　　假设有目标串T(t₀,t₁,t₂,t₃,……,t_n-1)和模式串P(p₀,p₁,p₂,p₃,……,p_m-1)，若使用BF算法进行模式匹配，第一轮比较时，若t_k≠p_k，则算法结束这轮比较_。

　　字符串T和P中第一个不相等的字符位置出现在位置k处，所以两串前k个字符是相等的，可以用字符串P(p₀,p₁,p₂,p₃,……,p_k-1)代替字符串T'(t₀,t₁,t₂,t₃,……,t_k-1)，于是原目标串可转化为T(p₀,p₁,p₂,p₃,……,p_k-1,t_k,...,t_n-1)。在进行第二次比较之前，算法同样把字符串P整体向后移动一个字符，此时，T与P的关系：

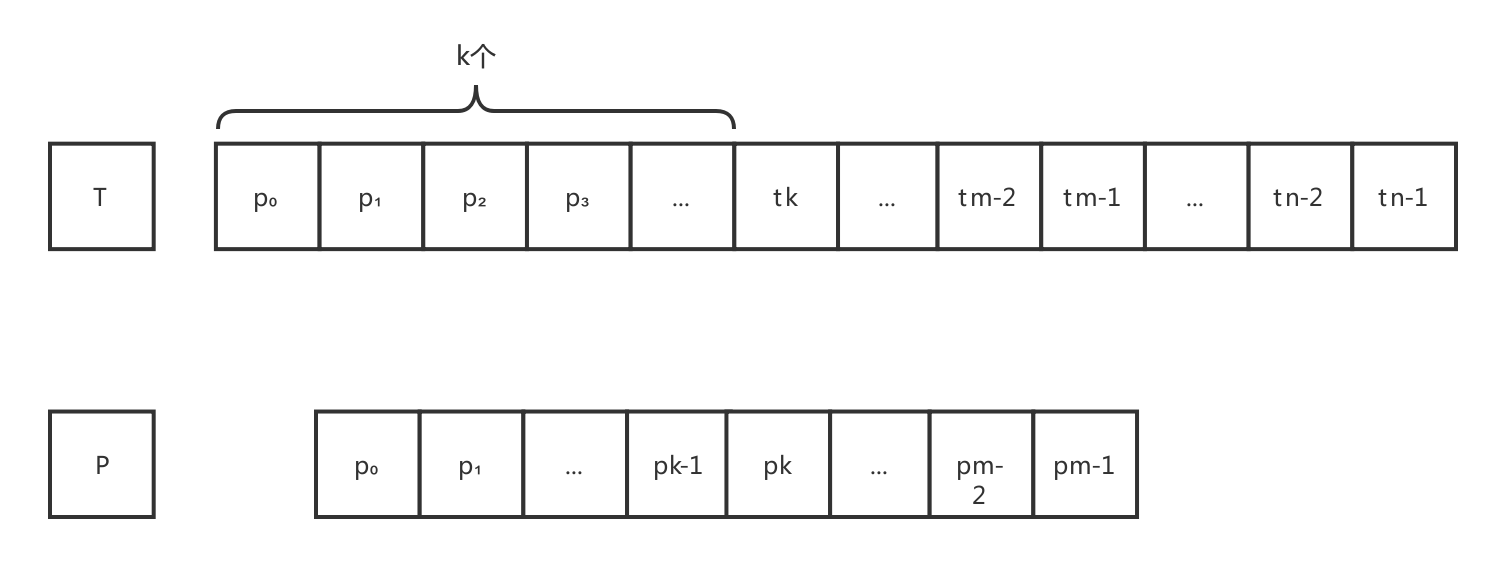
　　在上面的比较中，首先比较的是 P中的首字符p₀ 与 T中的第2个字符p₁，若与相等，则算法顺序比较 P中第2个字符P₁ 与 T中第3个字符P₂，若不相等，则算法将模式串P整体向后移动一个字符，此时T与P之间的关系：

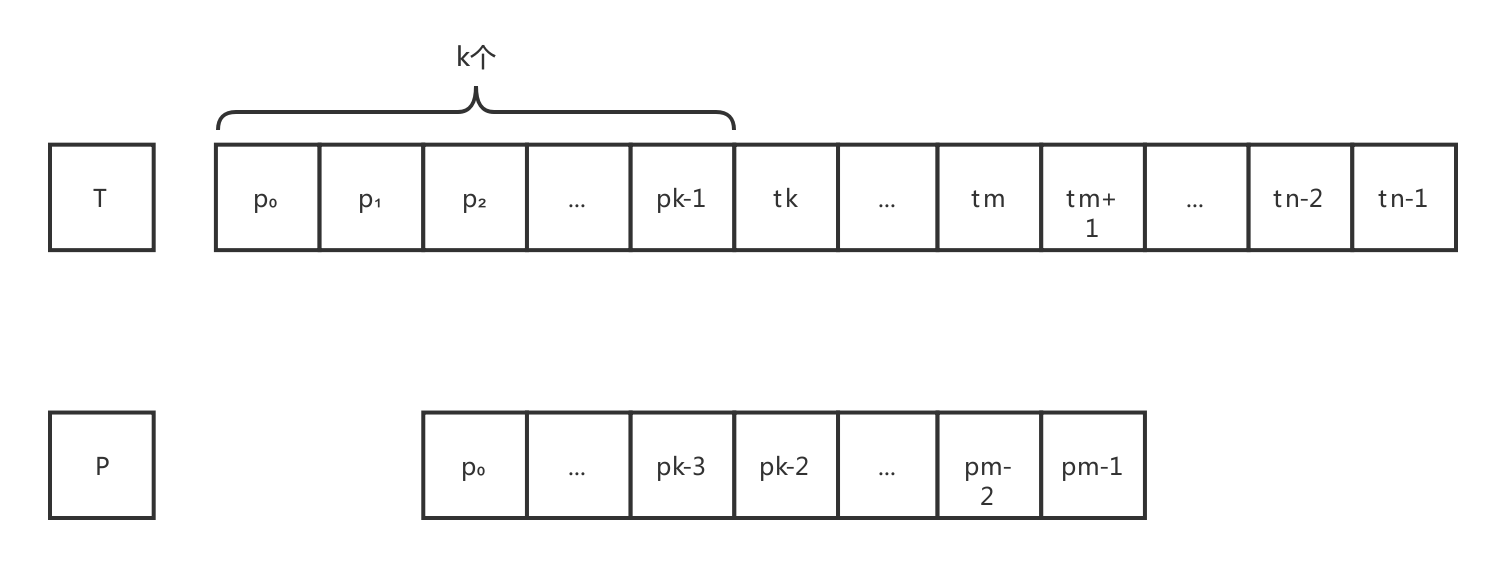
　　算法依照相同的次序，首先对 P中字符p₀ 与 T中字符p₂ 进行比较，若相等则顺序比较后续字符，若不相等，则把P整体向后移动一个字符。

　　从上面的流程描述，都是对模式串的字符作比较，所以MP算法先是计算出模式字符串（串P）中各个字符之间的关系，然后再依据此关系与目标字符串（串T）进行匹配。记录串P中各个字符之间的关系的函数也被称为字符串P的失效函数。

二、MP算法中模式串的失效函数

　　失效函数的定义域为 j∈{0, 1, 2, 3, 4, 5, 6}，也就是 0~Len(P)-1，Len(P)为串P的长度。

　　失效函数的值域的计算：对于 k∈{x | 0≤x<j}，且 k 满足 p₀ p_{1 …} p_k = p_j-k p_j-k+1 … p_j 的最大正整数。

　　对于模式串P“caatcat”的失效函数实例（不能满足条件的k不存在则为-1）：

j	0	1	2	3	4	5	6
p(j)	c	a	a	t	c	a	t
f(j)	-1	-1	-1	-1	0	1	-1

　　：

　　① 当 j = 0，由于 0≤k<0，所以满足条件的 k 并不存在，所以 j 取 0，f(0) = -1。

　　② 当 j = 4，k 的可能取值有 0,1,2,3，由于 p₀ = p₄，p₀p₁ ≠ p₃p₄，p₀p₁p₂ ≠ p₂p₃p₄ 以及 p₀p₁p₂p₃ ≠ p₁p₂p₃p₄，所以 f(4) = 0。

　　③ 当 j = 5，k 的可能取值有 0,1,2,3,4，同理 p₀ ≠ p₅，p₀p₁ = p₄p₅，p₀p₁p₂ ≠ p₃p₄p₅ ，p₀p₁p₂p₃ ≠ p₂p₃p₄p₅ 以及 p₀p₁p₂p₃p₄ ≠ p₁p₂p₃p₄p₅，所以 f(5) = 1。

　　得到字符串P的失效函数后，就可以应用 MP 算法对它进行匹配。

　　总结一下，上面所述的是在求字符串前缀后缀的部分匹配值，如例子②： j = 4，字符串的子串“caatc”，它的前缀表达式为{“c”，“ca”，“caa”，“caat”}，后缀表达式为{“aatc”，“atc”，“tc”，“c”}，所以由“caatc”的前缀后缀得到的部分匹配值为 “c”，对应的就是上面说的 0。

　　"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。模式串移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

三、MP函数使用失效函数对字符串进行匹配

　　假设模式串 P = “caatcat”，目标字符串 T = “ctcaatcacaatcat”。

　　在第一轮匹配前，首先把模式字符串P与目标字符串T从各自第一个字符起对齐。

　　有第一轮结果可知，模式字符串与目标字符串在第2个字符处发生失配。检测到适配后本轮结束，目标指针不发生回溯，仍指向失配的位置。由于失配发生在第2个字符处，此时 j = 1。所以模式P在下一轮匹配时的起始地址为 p_f(1-1)+1， 即P₀。

　　在第二轮比较中，由于模式字符串P在的第1个字符处发生失配，此时 j = 0，所以让目标的指针前进一位，模式的起始比较地址回到p_0。

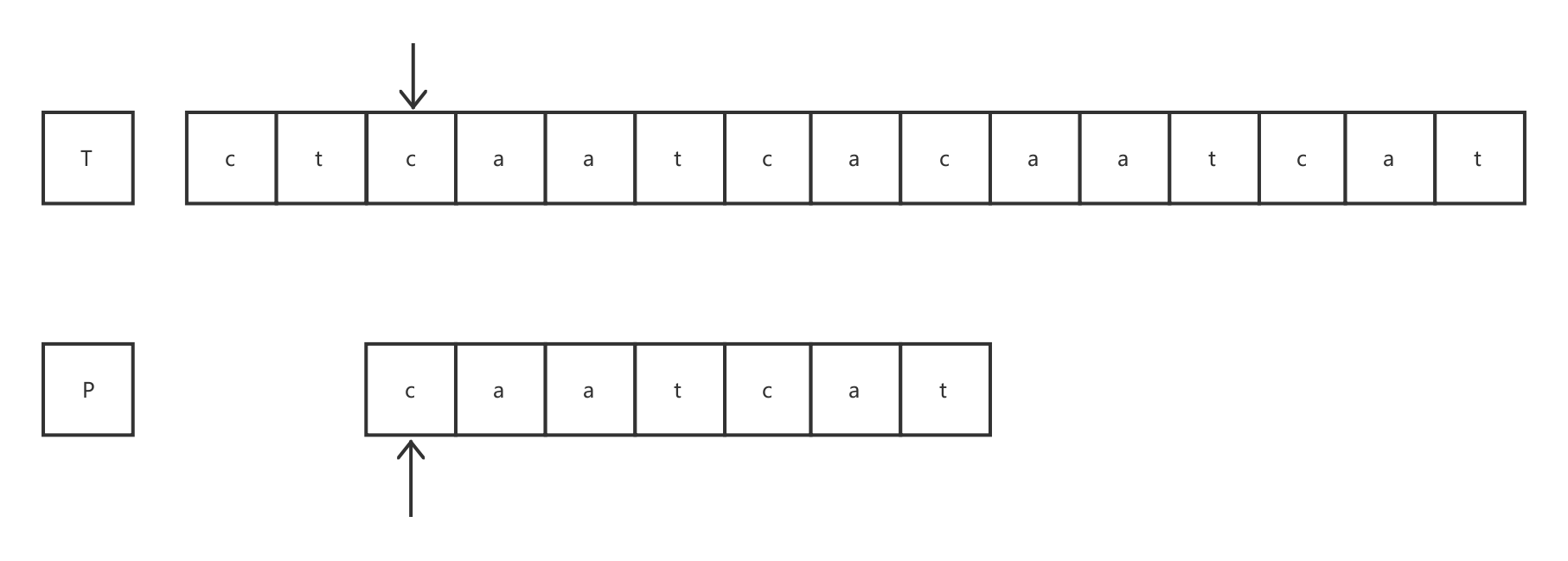
　　发现模式字符串P中的第7个字符处发生失配，此时 j = 6。可知模式字符串P在下一轮匹配时的起始比较地址为p_f(6-1)+1，即p₂。目标指针同样不发生回溯，仍指向发生失配的位置。

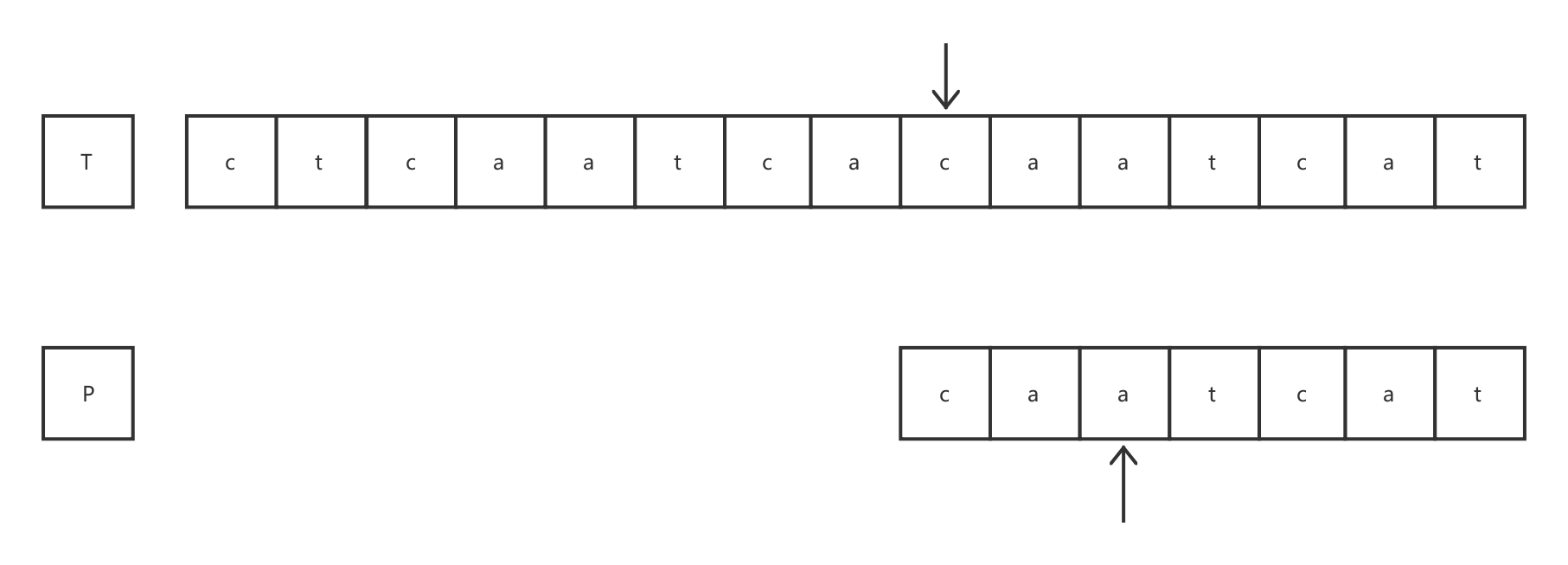
　　经过第4轮比较后，匹配成功。通过简单分析，MP算法的时间复杂度大致为O(m+n)，计算模式串的失效函数O(m)，利用失效函数进行匹配O(n)，m为模式串P的长度，n为目标串的长度。

　　MP算法利用模式串P的前缀后缀的部分匹配值，mpNext[j] 是下面代码用到的。这个数组存的是在失配的时候，目标指针不用变，模式串P指针的位置就存在mpNext数组中，因为在失配前的主串和模式串所对比那一段都是相同的，所以从计算的mpNext数组中找出下一次需要比较的模式串P中第几个位置字符，并和主串中发生失配的那个地方的字符作对比，这就是为什么MP算法利用先前计算的结果来避免频繁的回溯，加速匹配过程，mpNext数组的初衷就是找到模式串的某一部分前缀匹配到某一部分后缀。举个例子，比如上面那个j=6匹配过程图片中，失配发生在模式串P的第6位，主串在第8位（注意是从0开始），然后去从mpNext表中找到主串中第8个字符应该和模式串P的第2个字符比较，由上面那张图可见，主串失配前的两个字符都和模式串P的前两个字符相同，然后P(2)和T(8)比较，依然失配，然后再从mpNext找下一次P比较的位置，所以T(8)和P(0)比较。

　　”caatcat“的 mpNext 表如下：

 

j	0	1	2	3	4	5	6	7
p(j)	c	a	a	t	c	a	t
mpNext[j]	-1	0	0	0	0	1	2	0

 

四、代码

    /**
     * MP算法的失效函数
     *
     * @param x
     * @param m
     * @param mpNext 发生实配时，进行下一轮比较过程中模式P的起始比较地址
     */
    void preMp(char x[], int m, int mpNext[]) {
        int i, j;
        i = 0;
        j = mpNext[0] = -1;
        while (i < m) {
            while (j > -1 && x[i] != x[j])
                j = mpNext[j];
            mpNext[++i] = ++j;
        }
    }

    /**
     * MP算法
     * @param p 模式串
     * @param t 目标串
     */
    void mp(String p, String t) {
        int m = p.length();
        int n = t.length();
        if (m > n) {
            System.err.println("Unsuccessful match!");
            return;
        }

        char[] x = p.toCharArray();
        char[] y = t.toCharArray();

        int i = 0;
        int j = 0;
        int[] mpNext = new int[m+1];
        preMp(x, m, mpNext);

        while (j < n) {
            while (i > -1 && x[i] != y[j])
                i = mpNext[i];
            i++;
            j++;
            if (i >= m) {
                System.out.println("Matching index found at: " + (j - i + 1));
                i = mpNext[i];
            }
        }
    }