常见的查找算法(五):树表查找之二 ---- 红黑树
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为 红色 或 黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
下面是一个具体的红黑树的图例:

旋转
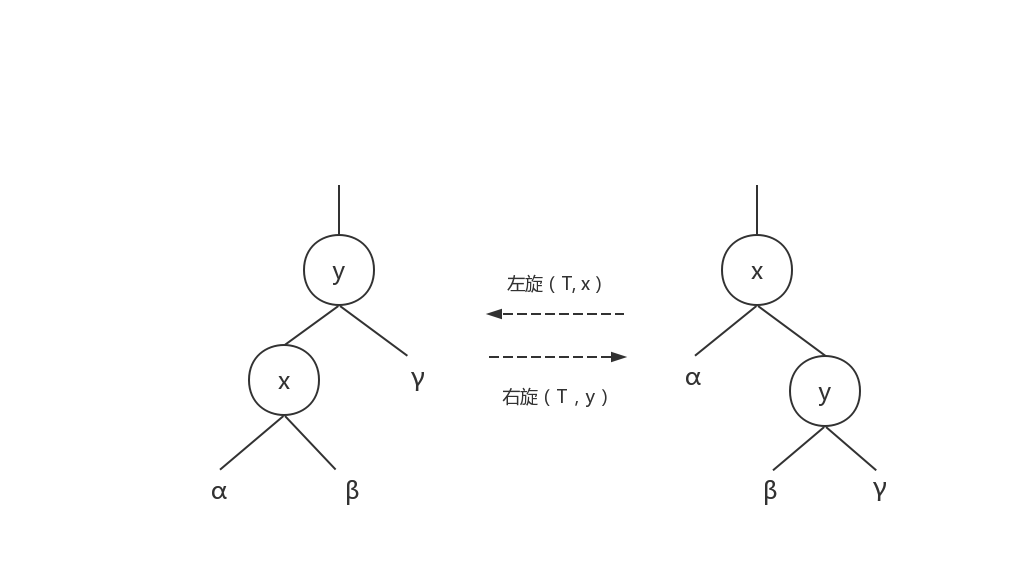
旋转是一种能保持二叉搜索树性质的搜索树局部操作。其中两种旋转分别为左旋和右旋:
在某个结点 x 上进行左旋时,假设它的右孩子为y而不是树的 T.nil 结点;x为其右孩子而不是 T.nil 结点的树内任意节点。
左旋以 x 到 y 的链为“支轴”进行,使得 y 成为该子树的新的根节点,x 成为 y 的左孩子,y 的左孩子变成 x 的右孩子;右旋与此相反。
左旋代码:
1 /** 2 * 左旋 3 * 左旋示意图(对节点x进行左旋): 4 * px px 5 * / / 6 * x y 7 * / \ --(左旋)--> / \ 8 * lx y x ry 9 * / \ / \ 10 * ly ry lx ly 11 * 12 * @param x 13 */ 14 private void leftRotate(RBTNode<T> x) { 15 RBTNode<T> y = x.right; // y是x的右节点 16 17 x.right = y.left; // 把x的左节点变为y的右节点 18 // 若y有左子节点,把y的左节点的父节点换成x 19 if (y.left != null) { 20 y.left.parent = x; 21 } 22 23 y.parent = x.parent; // y的父节点(原来是x)设为x的父节点 24 25 // 若x是根节点,y直接变根节点 26 if (x.parent == null) { 27 this.mRoot = y; 28 } else { 29 if (x.parent.left == x) { 30 x.parent.left = y; // 如果x是x父节点的左孩子,把x的父节点的左孩子指向y 31 } else { 32 x.parent.right = y; // 如果x是x父节点的右孩子,把x的父节点的右孩子指向y 33 } 34 } 35 36 y.left = x; // 将y的左节点指向x 37 x.parent = y; // 将x的父节点设为y 38 }
右旋代码:
1 /** 2 * 右旋,操作和左旋相反 3 * 右旋示意图(对节点y进行左旋): 4 * py py 5 * / / 6 * y x 7 * / \ --(右旋)--> / \ 8 * x ry lx y 9 * / \ / \ 10 * lx rx rx ry 11 * 12 * @param y 13 */ 14 private void rightRotate(RBTNode<T> y) { 15 RBTNode<T> x = y.left; // y的左孩子 16 17 y.left = x.right; 18 if (x.right != null) { 19 x.right.parent = y; 20 } 21 22 x.parent = y.parent; 23 24 if (y.parent == null) { 25 this.mRoot = x; 26 } else { 27 if (y.parent.left == y) { 28 y.parent.left = x; 29 } else { 30 y.parent.right = x; 31 } 32 } 33 34 x.right = y; 35 y.parent = x; 36 }
红黑树新结点插入代码:
就像一个普通的二叉搜索树一样,将新结点插入树中,并将其着为红色。之后为了能保证红黑的性质,还需要一个辅助代码对结点重新着色并且旋转。
1 /** 2 * 插入操作 3 * 4 * @param node 5 */ 6 private void insert(RBTNode<T> node) { 7 int result; 8 RBTNode<T> y = null; 9 RBTNode<T> x = this.mRoot; 10 11 // 查找树中插入点的父结点y的位置 12 while (x != null) { 13 y = x; // 注意这里,y不是空的 14 result = node.key.compareTo(x.key); 15 if (result < 0) { 16 x = x.left; 17 } else { 18 x = x.right; 19 } 20 } 21 22 node.parent = y; 23 if (y != null) { 24 result = node.key.compareTo(y.key); 25 if (result < 0) { 26 y.left = node; 27 } else { 28 y.right = node; 29 } 30 } else { 31 this.mRoot = node; 32 } 33 34 node.color = RED; 35 36 // 插入后修正树 37 insertFixUp(node); 38 }
辅助修正函数:
1 /** 2 * 红黑树插入修正函数 3 * 4 * @param node 5 */ 6 private void insertFixUp(RBTNode<T> node) { 7 RBTNode<T> parent, gparent; // 父节点,祖父节点 8 9 while (((parent = parentOf(node)) != null) && isRed(parent)) { 10 gparent = parentOf(parent); 11 12 // 父节点是祖父节点的左孩子 13 if (parent == gparent.left) { 14 RBTNode<T> uncle = gparent.right; // 叔叔节点,祖父的右节点 15 16 // ① 叔叔节点是红色的 17 if ((uncle != null) && isRed(uncle)) { 18 node.setColor(BLACK); 19 parent.setColor(BLACK); 20 gparent.setColor(RED); 21 node = gparent; 22 continue; 23 } 24 25 // ② 叔叔是黑色,且当前节点是右孩子 26 if (parent.right == node) { 27 RBTNode<T> tmp; 28 leftRotate(parent); 29 tmp = parent; 30 parent = node; 31 node = tmp; 32 } 33 34 // ③ 叔叔是黑色,且当前节点是左孩子 35 parent.setColor(BLACK); 36 gparent.setColor(RED); 37 rightRotate(gparent); 38 39 } else { // 父节点是祖父节点的右孩子 40 41 RBTNode<T> uncle = gparent.left; // 叔叔节点,祖父的左节点 42 43 // ① 叔叔节点是红色的 44 if ((uncle != null) && isRed(uncle)) { 45 uncle.setColor(BLACK); 46 parent.setColor(BLACK); 47 gparent.setColor(RED); 48 node = gparent; 49 continue; 50 } 51 52 // ② 叔叔是黑色,且当前节点是左孩子 53 if (parent.left == node) { 54 RBTNode<T> tmp; 55 rightRotate(parent); 56 tmp = parent; 57 parent = node; 58 node = tmp; 59 } 60 61 // ③ 叔叔是黑色,且当前节点是右孩子 62 parent.setColor(BLACK); 63 gparent.setColor(RED); 64 leftRotate(gparent); 65 } 66 } 67 68 this.mRoot.setColor(BLACK); 69 }
修正过程实例:
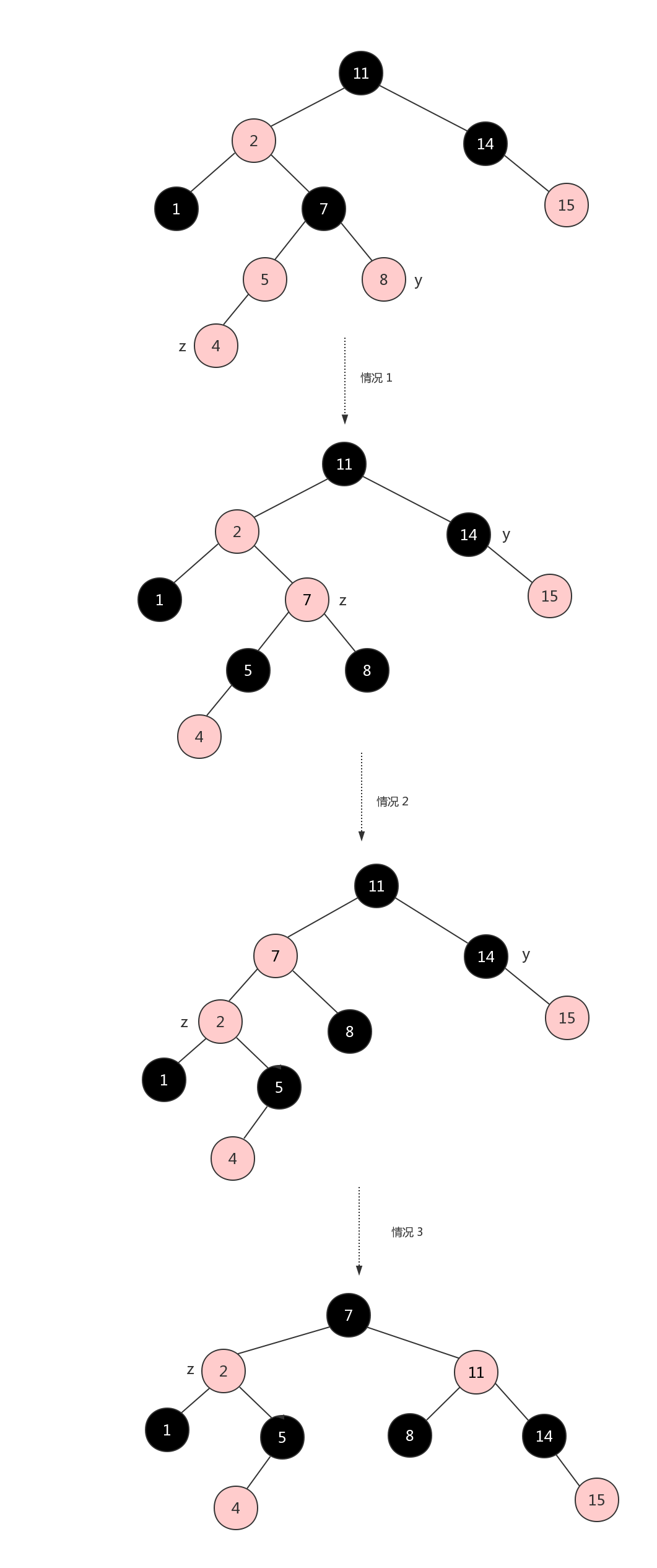
以下图中的 z 为插入后的结点,y 表示叔结点uncle,图中的每个子树的低端的节点是红黑树代码中的边界,边界中每个节点有黑色的哨兵没有画出来。
下面是介绍的是上面代码中 父节点是祖父节点的左孩子 的代码。
先看图中的第一个树,插入的 z 结点和 z.parent 父节点都是 RED,这违反了性质四。
情况 1(得到的是图中的第二个树):由于图中的第一个树中叔结点是红色,z 结点和 z.parent 父节点都是 RED,结点都要被重新着色,并沿着指针 z 上升;
情况 2(得到的是图中的第三个树):由于图中的第二个树中 z 及其父节点 z.parent 都为红色,其叔结点为黑色,左旋父节点 z.parent后得到;
情况 3(得到的是图中的第四个树):z 是其父节点的左孩子,重新着色后右旋的到图中的第四个树,这样之后就是合法的红黑树了。
分析红黑树的插入时间复杂度:
一颗具有 n 个节点的红黑树高度为O(log n),则按照一个普通的二叉查找树的方式插入结点需要花费 O(log n);修正代码中,当情况 1发生,指针 z沿着树上升2层,才会执行 while 循环,while 循环可能执行的总次数为 O(log n)。所以红黑树的插入的总的时间复杂度为 O(log n)。此外,插入算法中总的来说旋转次数不超过 2 次。
红黑树的删除:

1 /** 2 * 删除树中某个节点 3 * 4 * @param node 要删除的结点 5 */ 6 private void remove(RBTNode<T> node) { 7 RBTNode<T> child, parent; 8 boolean color; 9 10 // 要删除的结点node有2个子结点 11 if ((node.left != null) && (node.right != null)) { 12 RBTNode<T> replace = node; 13 14 // 寻找后继结点 15 replace = replace.right; 16 while (replace.left != null) { 17 replace = replace.left; 18 } 19 20 // 判断删除的结点是不是根结点 21 if (parentOf(node) != null) { 22 if (parentOf(node).left == node) { 23 parentOf(node).left = replace; 24 } else { 25 parentOf(node).right = replace; 26 } 27 } else { 28 this.mRoot = replace; 29 } 30 31 32 child = replace.right; // 后继结点的右孩子?左孩子呢?左孩子有早就是后继结点了,所以直接看后继结点还有没有右孩子 33 parent = parentOf(replace); // 后继结点的父结点 34 color = replace.color; // 后继结点的颜色 35 36 // 要删除的结点node是后继结点的父结点 37 if (parent == node) { 38 parent = replace; // 这里应该后继结点直接替换node,留下后继结点的右子树 39 } else { // 后继结点的父结点不是要删除的结点node 40 // 后继结点的孩子不为空 41 if (child != null) 42 child.setParent(parent); // 把<后继结点的右孩子>的<父结点>设为<后继结点的父结点> 43 parent.left = child; // <后继结点的父结点>的<左孩子>指向<后继结点的右孩子> 44 45 replace.right = node.right; // 后继结点的右孩子指向删除结点的右子树 46 node.right.setParent(replace); //删除结点的右子树的父结点设置为后继结点 47 } 48 49 replace.parent = node.parent; 50 replace.color = node.color; 51 replace.left = node.left; 52 node.left.parent = replace; 53 54 if (color == BLACK) 55 removeFixup(child, parent); 56 57 node = null; 58 59 return; 60 } 61 62 // 选一个要删除的结点的孩子 63 if (node.left != null) { 64 child = node.left; 65 } else { 66 child = node.right; 67 } 68 69 parent = node.parent; 70 color = node.color; 71 72 // 要删除的结点的孩子不为空 73 if (child != null) 74 child.parent = parent; 75 76 // 要删除的结点的父结点是不是树根 77 if (parent != null) { 78 if (parent.left == node) { 79 parent.left = child; 80 } else { 81 parent.right = child; 82 } 83 } else { 84 this.mRoot = child; 85 } 86 87 if (color == BLACK) 88 removeFixup(child, parent); 89 90 node = null; 91 }
删除修正函数:

1 /** 2 * 删除修正函数 3 * 4 * @param x 5 * @param parent 6 */ 7 private void removeFixup(RBTNode<T> x, RBTNode<T> parent) { 8 RBTNode<T> w; 9 10 while ((x == null || isBlack(x)) && (x != this.mRoot)) { 11 if (parent.left == x) { 12 w = parent.right; 13 14 // ① x的兄弟结点w是红色的 15 if (isRed(w)) { 16 w.setColor(BLACK); // w染黑 17 parent.setColor(RED); 18 leftRotate(parent); 19 w = parent.right; 20 } 21 22 // ② x的兄弟结点w是黑色的,而且w的两个孩子结点都是黑色的 23 if ((w.left == null || isBlack(w.left)) && 24 (w.right == null || isBlack(w.right))) { 25 w.setColor(RED); 26 x = parent; 27 parent = parentOf(x); 28 29 } else { 30 31 // ③ x的兄弟结点w是黑色的,w的右孩子是黑色的,w的左孩子是红色的 32 if ((w.right == null || isBlack(w.right)) && 33 (w.left == null || isBlack(w.left))) { 34 w.left.setColor(BLACK); 35 w.setColor(RED); 36 rightRotate(w); 37 w = parent.right; 38 } 39 40 // ④ x的兄弟结点w是黑色的,w的右孩子是红色的 41 w.setColor(parent.color); 42 parent.setColor(BLACK); 43 w.right.setColor(BLACK); 44 leftRotate(parent); 45 x = this.mRoot; 46 47 break; 48 } 49 50 } else { 51 52 w = parent.left; 53 // ① x的兄弟结点w是红色的 54 if (isRed(w)) { 55 w.setColor(BLACK); 56 parent.setColor(RED); 57 rightRotate(parent); 58 w = parent.left; 59 } 60 61 // ② x的兄弟结点w是黑色的,而且w的两个孩子结点都是黑色的 62 if ((w.left == null || isBlack(w.left)) && 63 (w.right == null || isBlack(w.right))) { 64 w.setColor(RED); 65 x = parent; 66 parent = parentOf(x); 67 } else { 68 69 // ③ x的兄弟结点w是黑色的,w的右孩子是黑色的,w的左孩子是红色的 70 if (w.left == null || isBlack(w.left)) { 71 w.right.setColor(BLACK); 72 w.setColor(RED); 73 leftRotate(w); 74 w = parent.left; 75 } 76 77 // ④ x的兄弟结点w是黑色的,w的右孩子是红色的 78 w.setColor(parent.color); 79 parent.setColor(BLACK); 80 w.left.setColor(BLACK); 81 rightRotate(parent); 82 x = this.mRoot; 83 84 break; 85 } 86 } 87 } 88 89 if (x != null) 90 x.setColor(BLACK); 91 }
红黑树总的代码(包含测试代码):

1 package tree; 2 3 /** 4 * @program: MyPractice 5 * @description: 红黑树 6 * @author: Mr.Wu 7 * @create: 2019-08-28 17:19 8 **/ 9 public class RBTree<T extends Comparable<T>> { 10 // 根节点 11 private RBTNode<T> mRoot; 12 13 private static final boolean RED = false; 14 private static final boolean BLACK = true; 15 16 private static final int a[] = {10, 40, 30, 60, 90, 70, 20, 50, 80}; 17 private static final boolean mDebugInsert = false; 18 private static final boolean mDebugDelete = true; 19 20 /** 21 * 左旋 22 * 左旋示意图(对节点x进行左旋): 23 * px px 24 * / / 25 * x y 26 * / \ --(左旋)--> / \ 27 * lx y x ry 28 * / \ / \ 29 * ly ry lx ly 30 * 31 * @param x 32 */ 33 private void leftRotate(RBTNode<T> x) { 34 RBTNode<T> y = x.right; // y是x的右节点 35 36 x.right = y.left; // 把y的左节点变为x的右节点 37 // 若y有左子节点,把y的左节点的父节点换成x 38 if (y.left != null) { 39 y.left.parent = x; 40 } 41 42 y.parent = x.parent; // y的父节点(原来是x)设为x的父节点 43 44 // 若x是根节点,y直接变根节点 45 if (x.parent == null) { 46 this.mRoot = y; 47 } else { 48 if (x.parent.left == x) { 49 x.parent.left = y; // 如果x是x父节点的左孩子,把x的父节点的左孩子指向y 50 } else { 51 x.parent.right = y; // 如果x是x父节点的右孩子,把x的父节点的右孩子指向y 52 } 53 } 54 55 y.left = x; // 将y的左节点指向x 56 x.parent = y; // 将x的父节点设为y 57 } 58 59 /** 60 * 右旋,操作和左旋相反 61 * 右旋示意图(对节点y进行左旋): 62 * py py 63 * / / 64 * y x 65 * / \ --(右旋)--> / \ 66 * x ry lx y 67 * / \ / \ 68 * lx rx rx ry 69 * 70 * @param y 71 */ 72 private void rightRotate(RBTNode<T> y) { 73 RBTNode<T> x = y.left; // y的左孩子 74 75 y.left = x.right; 76 if (x.right != null) { 77 x.right.parent = y; 78 } 79 80 x.parent = y.parent; 81 82 if (y.parent == null) { 83 this.mRoot = x; 84 } else { 85 if (y.parent.left == y) { 86 y.parent.left = x; 87 } else { 88 y.parent.right = x; 89 } 90 } 91 92 x.right = y; 93 y.parent = x; 94 } 95 96 /** 97 * 插入结点 98 * 99 * @param key 100 */ 101 public void insert(T key) { 102 RBTNode<T> node = new RBTNode<>(BLACK, key, null, null, null); 103 if (node != null) { 104 insert(node); 105 } 106 } 107 108 /** 109 * 插入操作 110 * 111 * @param node 112 */ 113 private void insert(RBTNode<T> node) { 114 int result; 115 RBTNode<T> y = null; 116 RBTNode<T> x = this.mRoot; 117 118 // 查找树中插入点的父结点y的位置 119 while (x != null) { 120 y = x; // 注意这里,y不是空的 121 result = node.key.compareTo(x.key); 122 if (result < 0) { 123 x = x.left; 124 } else { 125 x = x.right; 126 } 127 } 128 129 node.parent = y; 130 if (y != null) { 131 result = node.key.compareTo(y.key); 132 if (result < 0) { 133 y.left = node; 134 } else { 135 y.right = node; 136 } 137 } else { 138 this.mRoot = node; 139 } 140 141 node.color = RED; 142 143 // 插入后修正树 144 insertFixUp(node); 145 } 146 147 /** 148 * 红黑树插入修正函数 149 * 150 * @param node 151 */ 152 private void insertFixUp(RBTNode<T> node) { 153 RBTNode<T> parent, gparent; // 父节点 与 祖父节点 154 155 while (((parent = parentOf(node)) != null) && isRed(parent)) { 156 gparent = parentOf(parent); 157 158 // 父节点是祖父节点的左孩子 159 if (parent == gparent.left) { 160 RBTNode<T> uncle = gparent.right; // 叔叔节点,祖父的右节点 161 162 // ① 叔叔节点是红色的 163 if ((uncle != null) && isRed(uncle)) { 164 node.setColor(BLACK); 165 parent.setColor(BLACK); 166 gparent.setColor(RED); 167 node = gparent; 168 continue; 169 } 170 171 // ② 叔叔是黑色,且当前节点是右孩子 172 if (parent.right == node) { 173 RBTNode<T> tmp; 174 leftRotate(parent); 175 tmp = parent; 176 parent = node; 177 node = tmp; 178 } 179 180 // ③ 叔叔是黑色,且当前节点是左孩子 181 parent.setColor(BLACK); 182 gparent.setColor(RED); 183 rightRotate(gparent); 184 185 } else { // 父节点是祖父节点的右孩子 186 187 RBTNode<T> uncle = gparent.left; // 叔叔节点,祖父的左节点 188 189 // ① 叔叔节点是红色的 190 if ((uncle != null) && isRed(uncle)) { 191 uncle.setColor(BLACK); 192 parent.setColor(BLACK); 193 gparent.setColor(RED); 194 node = gparent; 195 continue; 196 } 197 198 // ② 叔叔是黑色,且当前节点是左孩子 199 if (parent.left == node) { 200 RBTNode<T> tmp; 201 rightRotate(parent); 202 tmp = parent; 203 parent = node; 204 node = tmp; 205 } 206 207 // ③ 叔叔是黑色,且当前节点是右孩子 208 parent.setColor(BLACK); 209 gparent.setColor(RED); 210 leftRotate(gparent); 211 } 212 } 213 214 this.mRoot.setColor(BLACK); 215 } 216 217 /** 218 * 删除树中某个值 219 * 220 * @param key 221 */ 222 public void remove(T key) { 223 RBTNode<T> node; 224 225 if ((node = search(mRoot, key)) != null) 226 remove(node); 227 } 228 229 /** 230 * 删除树中某个节点 231 * 232 * @param node 要删除的结点 233 */ 234 private void remove(RBTNode<T> node) { 235 RBTNode<T> child, parent; 236 boolean color; 237 238 // 要删除的结点node有2个子结点 239 if ((node.left != null) && (node.right != null)) { 240 RBTNode<T> replace = node; 241 242 // 寻找后继结点 243 replace = replace.right; 244 while (replace.left != null) { 245 replace = replace.left; 246 } 247 248 // 判断删除的结点是不是根结点 249 if (parentOf(node) != null) { 250 if (parentOf(node).left == node) { 251 parentOf(node).left = replace; 252 } else { 253 parentOf(node).right = replace; 254 } 255 } else { 256 this.mRoot = replace; 257 } 258 259 260 child = replace.right; // 后继结点的右孩子?左孩子呢?左孩子有早就是后继结点了,所以直接看后继结点还有没有右孩子 261 parent = parentOf(replace); // 后继结点的父结点 262 color = replace.color; // 后继结点的颜色 263 264 // 要删除的结点node是后继结点的父结点 265 if (parent == node) { 266 parent = replace; // 这里应该后继结点直接替换node,留下后继结点的右子树 267 } else { // 后继结点的父结点不是要删除的结点node 268 // 后继结点的孩子不为空 269 if (child != null) 270 child.setParent(parent); // 把<后继结点的右孩子>的<父结点>设为<后继结点的父结点> 271 parent.left = child; // <后继结点的父结点>的<左孩子>指向<后继结点的右孩子> 272 273 replace.right = node.right; // 后继结点的右孩子指向删除结点的右子树 274 node.right.setParent(replace); //删除结点的右子树的父结点设置为后继结点 275 } 276 277 replace.parent = node.parent; 278 replace.color = node.color; 279 replace.left = node.left; 280 node.left.parent = replace; 281 282 if (color == BLACK) 283 removeFixup(child, parent); 284 285 node = null; 286 287 return; 288 } 289 290 // 选一个要删除的结点的孩子 291 if (node.left != null) { 292 child = node.left; 293 } else { 294 child = node.right; 295 } 296 297 parent = node.parent; 298 color = node.color; 299 300 // 要删除的结点的孩子不为空 301 if (child != null) 302 child.parent = parent; 303 304 // 要删除的结点的父结点是不是树根 305 if (parent != null) { 306 if (parent.left == node) { 307 parent.left = child; 308 } else { 309 parent.right = child; 310 } 311 } else { 312 this.mRoot = child; 313 } 314 315 if (color == BLACK) 316 removeFixup(child, parent); 317 318 node = null; 319 } 320 321 /** 322 * 删除修正函数 323 * 324 * @param x 325 * @param parent 326 */ 327 private void removeFixup(RBTNode<T> x, RBTNode<T> parent) { 328 RBTNode<T> w; 329 330 while ((x == null || isBlack(x)) && (x != this.mRoot)) { 331 if (parent.left == x) { 332 w = parent.right; 333 334 // ① x的兄弟结点w是红色的 335 if (isRed(w)) { 336 w.setColor(BLACK); // w染黑 337 parent.setColor(RED); 338 leftRotate(parent); 339 w = parent.right; 340 } 341 342 // ② x的兄弟结点w是黑色的,而且w的两个孩子结点都是黑色的 343 if ((w.left == null || isBlack(w.left)) && 344 (w.right == null || isBlack(w.right))) { 345 w.setColor(RED); 346 x = parent; 347 parent = parentOf(x); 348 349 } else { 350 351 // ③ x的兄弟结点w是黑色的,w的右孩子是黑色的,w的左孩子是红色的 352 if ((w.right == null || isBlack(w.right)) && 353 (w.left == null || isBlack(w.left))) { 354 w.left.setColor(BLACK); 355 w.setColor(RED); 356 rightRotate(w); 357 w = parent.right; 358 } 359 360 // ④ x的兄弟结点w是黑色的,w的右孩子是红色的 361 w.setColor(parent.color); 362 parent.setColor(BLACK); 363 w.right.setColor(BLACK); 364 leftRotate(parent); 365 x = this.mRoot; 366 367 break; 368 } 369 370 } else { 371 372 w = parent.left; 373 // ① x的兄弟结点w是红色的 374 if (isRed(w)) { 375 w.setColor(BLACK); 376 parent.setColor(RED); 377 rightRotate(parent); 378 w = parent.left; 379 } 380 381 // ② x的兄弟结点w是黑色的,而且w的两个孩子结点都是黑色的 382 if ((w.left == null || isBlack(w.left)) && 383 (w.right == null || isBlack(w.right))) { 384 w.setColor(RED); 385 x = parent; 386 parent = parentOf(x); 387 } else { 388 389 // ③ x的兄弟结点w是黑色的,w的右孩子是黑色的,w的左孩子是红色的 390 if (w.left == null || isBlack(w.left)) { 391 w.right.setColor(BLACK); 392 w.setColor(RED); 393 leftRotate(w); 394 w = parent.left; 395 } 396 397 // ④ x的兄弟结点w是黑色的,w的右孩子是红色的 398 w.setColor(parent.color); 399 parent.setColor(BLACK); 400 w.left.setColor(BLACK); 401 rightRotate(parent); 402 x = this.mRoot; 403 404 break; 405 } 406 } 407 } 408 409 if (x != null) 410 x.setColor(BLACK); 411 } 412 413 private boolean isRed(RBTNode<T> node) { 414 return (node != null) && (node.color == RED); 415 } 416 417 private boolean isBlack(RBTNode<T> node) { 418 return !isRed(node); 419 } 420 421 /** 422 * 二叉查找,递归 423 * 424 * @param x 425 * @param key 426 * @return 427 */ 428 private RBTNode<T> search(RBTNode<T> x, T key) { 429 if (x == null) 430 return x; 431 432 int result = key.compareTo(x.key); 433 if (result < 0) { 434 return search(x.left, key); 435 } else if (result > 0) { 436 return search(x.right, key); 437 } else { 438 return x; 439 } 440 } 441 442 /** 443 * 找结点的父节点 444 * 445 * @param node 446 * @return 447 */ 448 private RBTNode<T> parentOf(RBTNode<T> node) { 449 return (node != null) ? node.parent : null; 450 } 451 452 /** 453 * 置空树 454 */ 455 public void clear() { 456 destroy(mRoot); 457 mRoot = null; 458 } 459 460 /** 461 * 销毁树 462 * 463 * @param tree 464 */ 465 private void destroy(RBTNode<T> tree) { 466 if (tree == null) { 467 return; 468 } 469 if (tree.left != null) { 470 destroy(tree.left); 471 } 472 if (tree.right != null) { 473 destroy(tree.right); 474 } 475 476 tree = null; 477 } 478 479 /** 480 * 先序遍历 481 */ 482 public void preOrder() { 483 preOrder(mRoot); 484 } 485 486 /** 487 * 先序遍历 488 * 489 * @param tree 490 */ 491 private void preOrder(RBTNode<T> tree) { 492 if (tree != null) { 493 System.out.print(tree.key + " "); 494 preOrder(tree.left); 495 preOrder(tree.right); 496 } 497 } 498 499 public void inOrder() { 500 inOrder(mRoot); 501 } 502 503 /** 504 * 中序遍历 505 * 506 * @param tree 507 */ 508 private void inOrder(RBTNode<T> tree) { 509 if (tree != null) { 510 inOrder(tree.left); 511 System.out.print(tree.key + " "); 512 inOrder(tree.right); 513 } 514 } 515 516 /** 517 * 后序遍历 518 */ 519 public void postOrder() { 520 postOrder(mRoot); 521 } 522 523 /** 524 * 后序遍历 525 * 526 * @param tree 527 */ 528 private void postOrder(RBTNode<T> tree) { 529 if (tree != null) { 530 postOrder(tree.left); 531 postOrder(tree.right); 532 System.out.print(tree.key + " "); 533 } 534 } 535 536 /** 537 * 打印树的信息 538 */ 539 public void print() { 540 if (mRoot != null) { 541 print(mRoot, mRoot.key, 0); 542 } 543 } 544 545 /** 546 * 打印树的详细信息 547 * 548 * @param tree 549 * @param key 550 * @param direction 551 */ 552 private void print(RBTNode<T> tree, T key, int direction) { 553 if (tree != null) { 554 if (direction == 0) { 555 System.out.printf("%2d(B) is root\n", tree.key); 556 } else { 557 System.out.printf("%2d(%s) is %2d's %6s child\n", tree.key, isRed(tree) ? "R" : "B", 558 key, direction == 1 ? "right" : "left"); 559 } 560 print(tree.left, tree.key, -1); 561 print(tree.right, tree.key, 1); 562 } 563 } 564 565 /** 566 * 找树中值最大的结点 567 * 568 * @param tree 569 * @return 570 */ 571 private RBTNode<T> maximum(RBTNode<T> tree) { 572 if (tree == null) 573 return null; 574 while (tree.right != null) 575 tree = tree.right; 576 return null; 577 } 578 579 /** 580 * 找树中值最大的结点 581 * 582 * @return 583 */ 584 public T maximum() { 585 RBTNode<T> p = maximum(mRoot); 586 if (p != null) 587 return p.key; 588 return null; 589 } 590 591 /** 592 * 找树中值最小的结点 593 * 594 * @param tree 595 * @return 596 */ 597 private RBTNode<T> minimum(RBTNode<T> tree) { 598 if (tree == null) 599 return null; 600 while (tree.left != null) 601 tree = tree.left; 602 return tree; 603 } 604 605 /** 606 * 找树中值最小的结点 607 */ 608 public T minimum() { 609 RBTNode<T> p = minimum(mRoot); 610 if (p != null) 611 return p.key; 612 return null; 613 } 614 615 /** 616 * 测试主函数 617 * @param args 618 */ 619 public static void main(String[] args) { 620 int i, length = a.length; 621 RBTree<Integer> tree = new RBTree<>(); 622 623 System.out.printf("== 原始数据: "); 624 for (i = 0; i < length; i++) 625 System.out.printf("%d ", a[i]); 626 System.out.printf("\n"); 627 628 for (i = 0; i < length; i++) { 629 tree.insert(a[i]); 630 // 设置mDebugInsert=true,测试"添加函数" 631 if (mDebugInsert) { 632 System.out.printf("== 添加节点: %d\n", a[i]); 633 System.out.printf("== 树的详细信息: \n"); 634 tree.print(); 635 System.out.printf("\n"); 636 } 637 } 638 639 System.out.printf("== 前序遍历: "); 640 tree.preOrder(); 641 642 System.out.printf("\n== 中序遍历: "); 643 tree.inOrder(); 644 645 System.out.printf("\n== 后序遍历: "); 646 tree.postOrder(); 647 648 System.out.printf("\n"); 649 650 System.out.printf("== 最小值: %s\n", tree.minimum()); 651 System.out.printf("== 最大值: %s\n", tree.maximum()); 652 System.out.printf("== 树的详细信息: \n"); 653 tree.print(); 654 655 System.out.printf("\n"); 656 657 // 设置mDebugDelete=true,测试"删除函数" 658 if (mDebugDelete) { 659 for (i = 0; i < length; i++) { 660 tree.remove(a[i]); 661 662 System.out.printf("== 删除节点: %d\n", a[i]); 663 System.out.printf("== 树的详细信息: \n"); 664 tree.print(); 665 666 System.out.printf("\n"); 667 } 668 } 669 670 // 销毁二叉树 671 tree.clear(); 672 } 673 674 /** 红黑树结点 RBTNode **/ 675 public class RBTNode<T extends Comparable<T>> { 676 boolean color; // 颜色 677 T key; // 关键字 678 RBTNode<T> left; 679 RBTNode<T> right; 680 RBTNode<T> parent; 681 682 public RBTNode(boolean color, T key, RBTNode<T> left, RBTNode<T> right, RBTNode<T> parent) { 683 this.color = color; 684 this.key = key; 685 this.left = left; 686 this.right = right; 687 this.parent = parent; 688 } 689 690 public boolean isColor() { 691 return color; 692 } 693 694 public void setColor(boolean color) { 695 this.color = color; 696 } 697 698 public T getKey() { 699 return key; 700 } 701 702 public void setKey(T key) { 703 this.key = key; 704 } 705 706 public RBTNode<T> getLeft() { 707 return left; 708 } 709 710 public void setLeft(RBTNode<T> left) { 711 this.left = left; 712 } 713 714 public RBTNode<T> getRight() { 715 return right; 716 } 717 718 public void setRight(RBTNode<T> right) { 719 this.right = right; 720 } 721 722 public RBTNode<T> getParent() { 723 return parent; 724 } 725 726 public void setParent(RBTNode<T> parent) { 727 this.parent = parent; 728 } 729 } 730 }




