常见的排序算法（三）：快速排序

　　快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），简称快排，一种排序算法，使用了分治思想来进行数组排序，数组划分为两个子数组A[p, ..., q-1]和A[q+1, ..., r]，A[p, ..., q-1]中的每一个元素都小于A[q]，A[q+1, ..., r]中的每一个元素都大于A[q]，计算下标q对划分数组有很大影响。在平均状况下，排序n个项目要O(n·logn)次比较。在最坏状况下则需要O(n²)次比较，但这种状况并不常见。事实上，快速排序O(n·logn)通常明显比其他算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地达成。

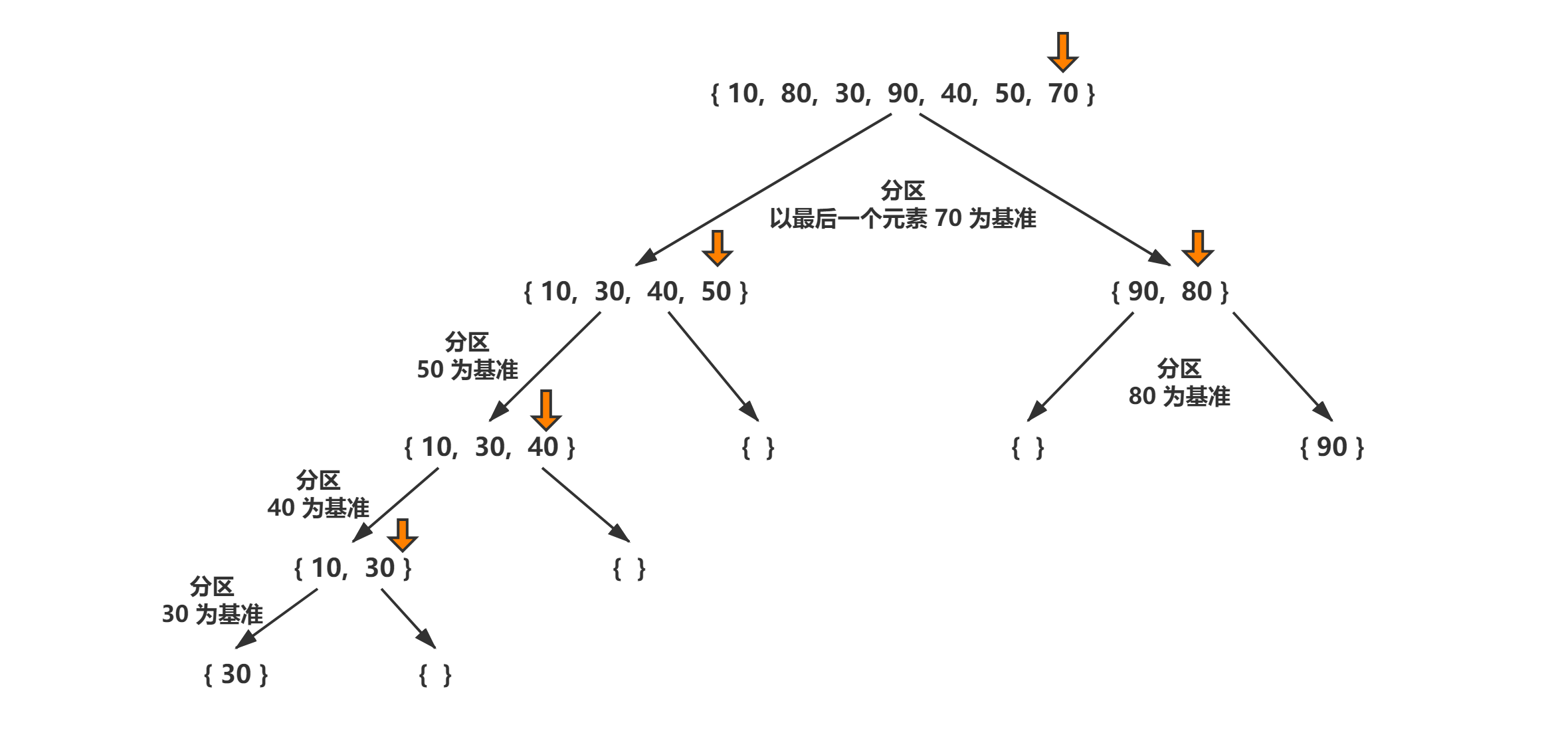
　　快排算法的主要思想是分治法，其关键过程就是分区。分区的目标是，给定一个数组和该数组的一个元素 pivot 作为主元（基准），之后都是围绕着主元来划分子数组。将 pivot 元素发在已排序数组中的正确位置，并将所有较小的元素（< pivot ）放在 pivot 之前，并把所有较大的元素（>pivot ）放在 pivot 之后。这些操作都在线性的时间内完成。

　　这里分区的方法是选取最后一个元素作为主元。注意，分区的实现有多种，不是一定要选最最后那个元素。

    /**
     * 快速排序的分区算法
     *
     * @param arrays 排序的数组
     * @param left 当前左边界
     * @param right 当前右边界
     * @return 分区索引
     */
    private static int partition(int[] arrays, int left, int right) {
        int pivot = arrays[right];  // 把当前数组最右边那个作为主元pivot element
        int i = left - 1;   // 记录较小元素的索引, 最后主元pivot element需要放到这个i下标的后一位
        // 把比主元大的元素放右边, 把比主元小的元素放左边
        for (int j = left; j < right; j++) {
            // 如果元素小于基准pivot, i的计数加1
            if (arrays[j] < pivot) {
                i++;
                // 当遇到比主元小的元素时, 前一位可能是比基准大的元素, 这时需要调整比基准大的元素和比基准小的元素之间的位置
                // 这就是为什么要记录较小元素的位置索引的原因
                swap(arrays, i, j);
            }
        }
        swap(arrays, i + 1, right);
        return i + 1;
    }

　　辅助交换函数swap()：

    public static void swap(int a[], int i, int j) {
        //所记录下的比主元大的位置（默认为0）当前比主元小的数的位置相同时跳过交换
        if (i == j)
            return;
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }

　　利用递归把数组一直分成两个小问题，直至分到数组只有一个元素。

    public static void quickSorts(int[] a, int left, int right) {
        if (left < right) {
            int q = partition(a, left, right);//返回初步筛选好的数组的主元的位置
            //根据主元的下标来递归调用，知道数组分为只有一个元素(left = right时)
            quickSorts(a, left, q - 1);
            quickSorts(a, q + 1, right);
        }
    }

　　通常，QuickSort 进行时间复杂度分析如下：

　　　　T(n) = T(k) + T(n - k - 1) + θ(n)

　　等号右边前两个是属于递归调用的，最后那一个是属于分区过程的。k 是小于主元的元素数。

　　QuickSort 花费的时间取决于输入阵列和分区策略。以下有三种情况：

　　① 最坏情况：最坏的情况是发生在分区过程中始终选择最大或者最小元素作为主元时。如果说考虑上面说的分区策略，总是选择最后一个元素作为主元，则最坏的情况发生在数组已经在按升序或降序排序时。则以下是最坏的情况：

　　T(n) = T(0) + T(n - 1) + θ(n)

　　　　 = T(n - 1) + θ(n)

　　上述的重复进行后的复杂度是 θ(n²)。

　　② 最佳情况：最佳情况发生在分区过程始终选择中间元素作为主元时。

　　T(n) = 2·T(n / 2) + θ(n)

　　上述的复杂度是 θ(n·logn)。

　　③ 平均用例情况：

　　要进行平均用例分析，我们需要考虑数组的所有可能排列，并计算不容易看出来的每种排列的时间。

　　通过考虑分区将 O(n / 10) 元素放在一个集合中而 O(9n / 10) 元素放在另一个集合中的情况，可以得到平均情况的想法。

　　T(n) = T(n / 10) + T(9n / 10) + θ(n)

　　上述的复杂度也是 O(n·Logn)。

　　尽管 QuickSort 在最坏情况下的时间复杂度为 O(n²)，这比许多其他排序算法（例如 Merge Sort 和 Heap Sort）的时间复杂度要多，但 QuickSort 在实践中却更快，因为它的内部循环可以在大多数体系结构上有效地实现，并且在大多数情况下真实数据。通过更改数据透视表的选择，可以以不同的方式实现 QuickSort，因此对于给定类型的数据，最坏的情况很少发生。但是，当数据量巨大并存储在外部存储中时，通常认为合并排序更好。

　　快速排序算法是不稳定的，在这里描述的快排是一种 原址（in-place）排序算法，因为是同过递归实现的，仅使用额外的空间来存储递归函数调用。

　　测试算法：

    public static void main(String[] args) {
        int[] arr = {1, 111, 211, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22};//size=13

        QuickSort.quickSorts(arr, 0, arr.length - 1);

        for (int a : arr) {
            System.out.print(a + " ");
        }
    }