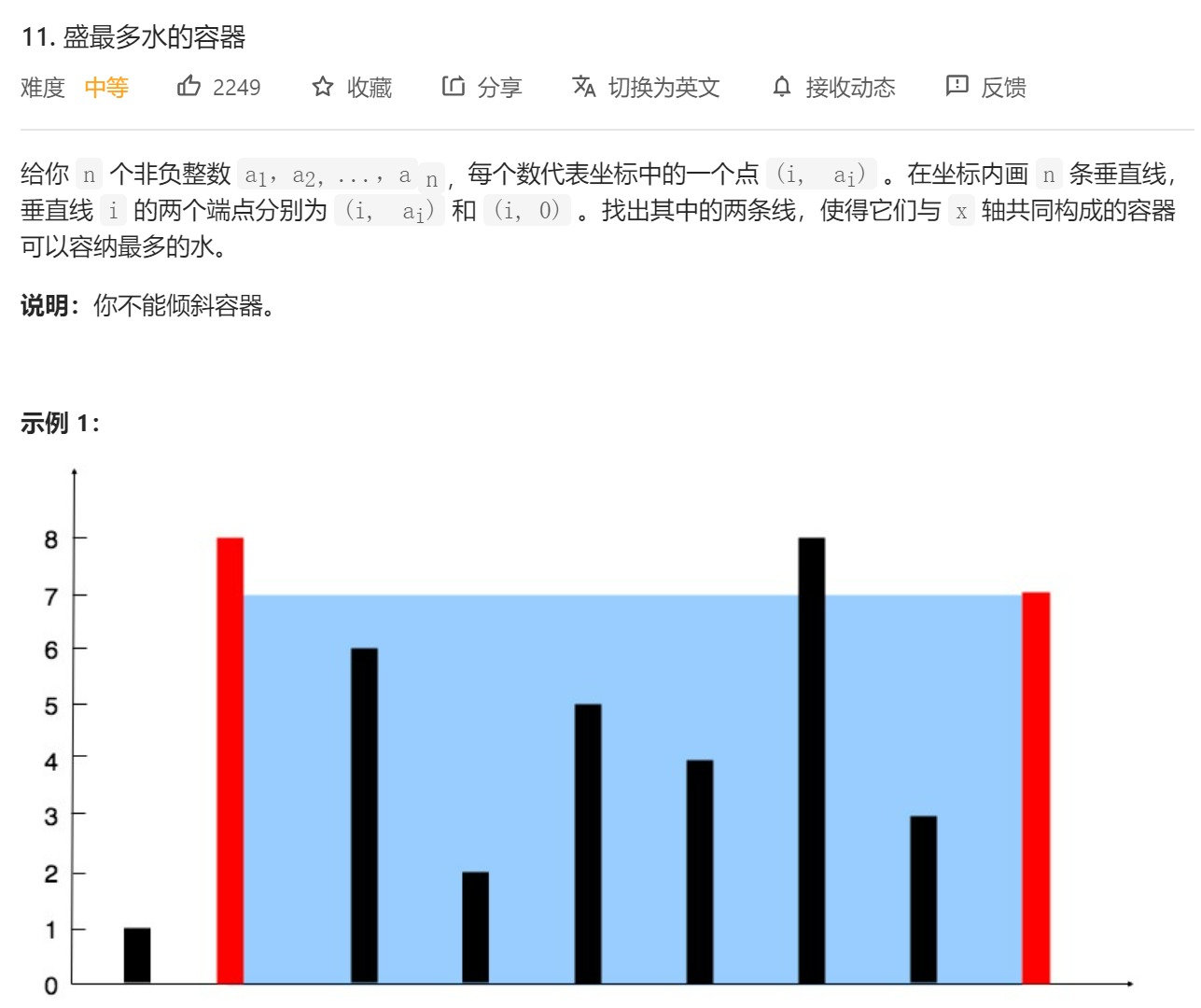
【LeetCode】11. 盛最多水的容器

木桶效应

一只木桶能盛多少水，并不取决于最长的那块木板，而是取决于最短的那块木板。

解题思路

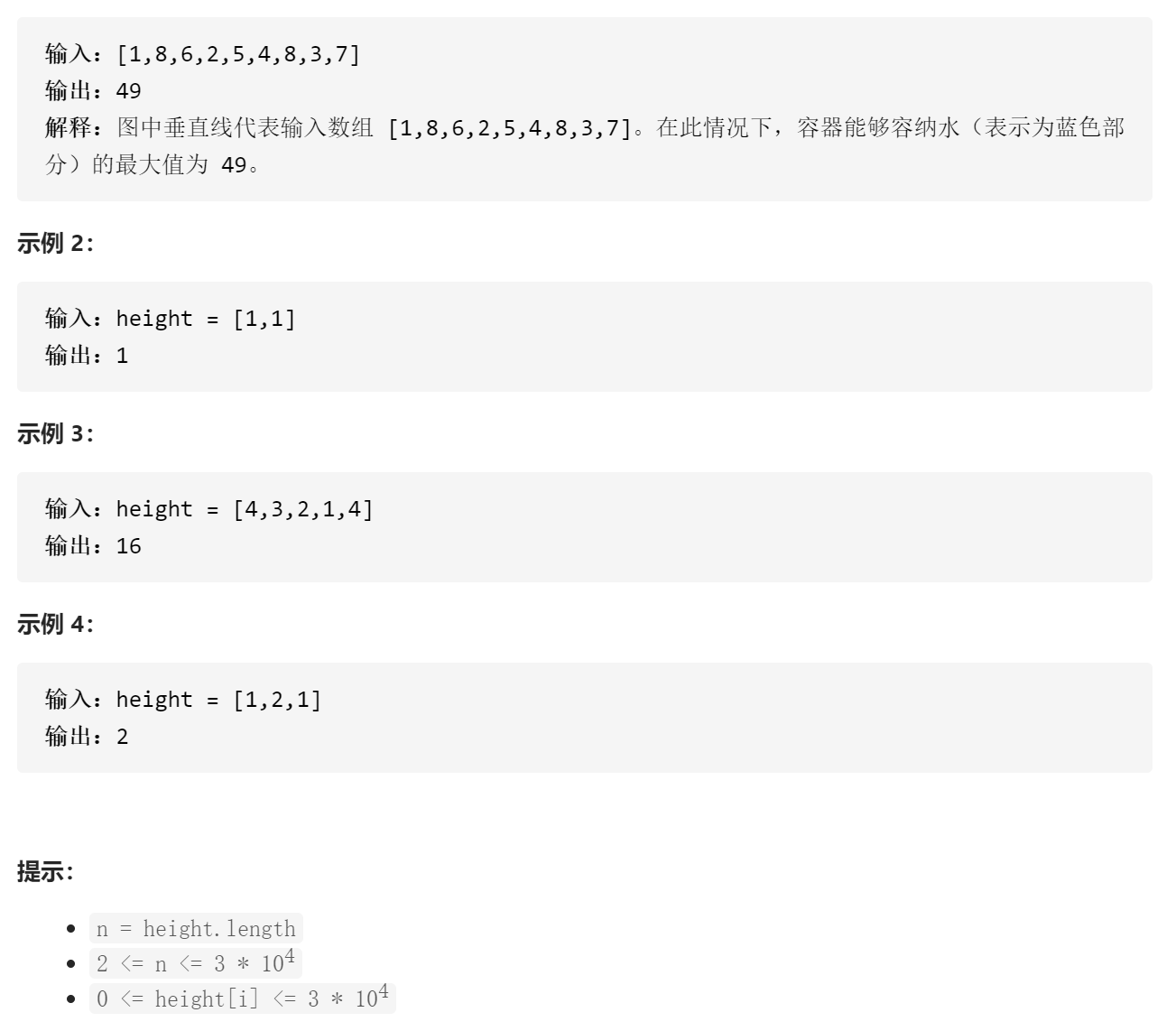
初始化left指针为左边界，right指针为右边界。首先获取短板的高度，即两个指针对应高度的较小值minHeight，由此计算容纳的水量为minHeight * (right - left)，然后更新最大值res，并将短板指针向内移动，重复这个过程直到双指针重合。

为什么移动短板指针

设容器最初可容纳的水量为x，短板指针为a，长板指针为b，宽度为w，则x = height[a] * w。
移动指针后，设容器可容纳的新水量为y，

1. 移动短板指针a，设移动后的指针为c。

• height[c] <= height[a]，则y = height[c] * (w - 1)，y一定小于x。
• height[c] > height[a]，则y = min(height[b], height[c]) * (w - 1)，y可能大于x。

2. 移动长板指针b，设移动后的指针为d。

• height[d] <= height[a]，则y = height[d] * (w - 1)，y一定小于x。
• height[d] > height[a]，则y = height[a] * (w - 1)，y一定小于x。

综上所述，只有移动短板指针才有可能得到最大值。

代码

class Solution {
    public int maxArea(int[] height) {
        int res = 0, left = 0, right = height.length - 1;
        while (left < right) {
            int minHeight = Math.min(height[left], height[right]);
            res = Math.max(res, minHeight * (right - left));
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return res;
    }
}

简化代码

class Solution {
    public int maxArea(int[] height) {
        int res = 0, left = 0, right = height.length - 1;
        while (left < right) {
            int minHeight = height[left] < height[right] ? height[left++] : height[right--];
            res = Math.max(res, minHeight * (right - left + 1));
        }
        return res;
    }
}

复杂度分析

• 时间复杂度：O(N)，其中N为数组的长度，最多遍历整个数组一次。
• 空间复杂度：O(1)，只需要额外的常数级别的空间。