算法---红黑树实现介绍（一）

一、概述

　　红黑树是一种经典的存储结构，就其本身来说是一个二叉查找树，只是在这个基础上，树的节点增加了一个属性用于表示颜色（红或黑）。通过限制从根节点到叶子的各个路径的节点着色的限制，来保证不会有哪个路径会比其它的路径长度超过2倍，从而红黑树是接近平衡的。

　　一直以来没有把红黑树完全理解，总觉得太难，望而生畏，最近下决心要弄清楚，也是花了很长时间，不过总算是明白了。记录下来以便更好的理解。

二、红黑树的特点

　　作为红黑树，需要有这5个限制，如下：

　　1）树中的每个节点，要么是红色，要么是黑色

　　2）树的根节点必须是黑色

　　3）叶子节点(NULL节点）的颜色为黑色

　　4）如果某个节点是红色，则其儿子节点必为黑色

　　5）从某节点到其子孙节点的所有路径上，黑节点的个数必须相同

 

　　这5个特点，也可以认为是约束条件，是判断树是否为红黑树的充要条件。看似不相关，其实都是为了达到控制路径长度的目标而设置的，对这些特点做下详细的解释。特点1就不解释了。

　　a）根节点为黑色及叶子节点为黑色:这个也是约定，当然我们也可以将这两个都规定为必须为红色，总之记住黑色是主旋律，红色是用来起间隔作用的。另外叶子节点指的最后一层节点，节点不包括数据，仅表示路径的结束。这样一来，所有的数据节点都有两个儿子，可能是两个数据节点，或者一个数据节点一个叶子节点，或者是两个叶子节点。而叶子节点则没有儿子了，它就是每个路径的最后一个节点。

　　b) 性质4和5具有递归性，通过这两个性质，则红黑树的任意子树都具备除了性质2）之外的其它红黑树特点，而根只有一个。所以这样限制后，为树的调整带来了便利，由于红节点的不连续性和黑节点个数的限制，使得任一两条路径的长度差不会超过2倍。最坏的两个路径差也是2倍（即一个路径上全是黑节点，另一个路径上红黑间隔）

三、树的旋转

　　树的旋转也是一个经典的算法了，不仅限于红黑树，是为了调整树的高度和平衡性而做的一种调整。分为左旋和右旋，这两种操作的逻辑是一样的，只是方向相反，所以我们这里只介绍一下左旋。

　　在对一个节点进行左旋时，我们要假定它是有非叶子节点的右孩子的，否则旋转没有意义，同样，在右旋时，我们认为它是有非叶子节点的左孩子的。

　　下面先给出一个左旋的直接示意图：

 

　　上图中，针对B节点进行左旋，其主要操作如下：

　　1）将B的右孩子设置为E的左孩子，对应E的左路孩子的父亲设置为B

　　2）将E的左孩子设置为B，E的父亲设置为B的父亲，B父亲原来指向B的孩子节点，指向E

　　3）B的父亲设置为E

 

　　我们再来看下Java代码的实现：

/**
 * 对节点P进行左旋，这里我们认为P就是上图的节点B
 **/
private void rotateLeft(Entry<K,V> p) {
        if (p != null) {
            Entry<K,V> r = p.right;//r为B的右孩子，即上图中的E
            p.right = r.left;//B的右孩子设置为E的左孩子，操作之后，B的右孩子由E变成了F
            if (r.left != null)
                r.left.parent = p;//对应，F的父亲由原来的E变成了B
            r.parent = p.parent;//E的父亲由原来的B变成B的父亲A
            if (p.parent == null)
                root = r; //B的父亲不为空，所以这一步不会执行
            else if (p.parent.left == p)
                p.parent.left = r; //如果B是其父亲的左孩子，则其父亲的左孩子指向E，上图中B为左孩子，所以走这个分支，A的左孩子变成E
            else
                p.parent.right = r;//B是其父亲的右孩子的话走这个分支
            r.left = p; //将E的左孩子（原来是F）变更为B
            p.parent = r; //将B的父亲（原来是A）变更为E
        }
    }

 

　　树的右旋也是类似，在此就不再说明了。

四、红黑树的添加

　　红黑树本身是一颗二叉查找树，即某个节点的值一定不小于其左孩子的值，且不大于其右孩子的值。当添加一个节点时，从根遍历，一定能找到一个合适的节点，使其成为当前节点的父节点，而当前节点则成为那个合适节点的左孩子或者是右孩子，取决于这两个节点的值之间的大小关系。

　　当添加一个节点时到一个已知的红黑树时，无论当前节点是什么颜色，红黑树的性质都可能被破坏，所以，添加完了之后，还需要通过一些步骤对树进行调整，使之重新成为一个红黑树。
　　所以，添加一个节点主要做这两件事：

　　1）从根遍历，找到一个合适的节点，作为新元素的父亲节点。

　　2）对树进行调整以使其重新满足红黑树的性质。

　　以下是在一个已有的红黑树中添加新节点23的情况，紫色的线表示查找路径。

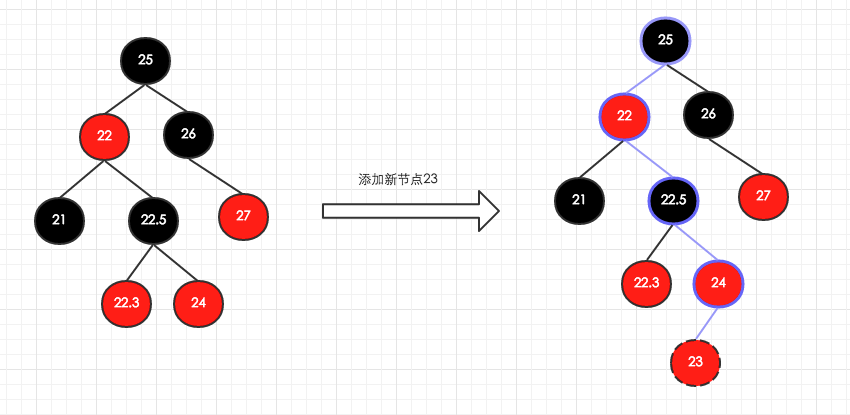
　　查找过程比较简单，就不列出代码了，接着看第二个问题，调整。

　　在添加一个新节点时，按约定，新节点的颜色为红色，既然要调整，我们必须要弄清楚添加了红节之后可能会导致哪些性质被破坏。很明显，新节点满足非红即黑的性质，叶子节点也是永远是黑色，且路径上的黑节点未增加，所以性质1，3，5不会被破坏，2，4可能被破坏，具体情况为：

　　a) 当原树为空树时，新节点为根，根不能为红色，所以性质2被破坏，这种情况比较好处理，直接将节点颜色置为黑色即可。

      b) 当父亲节点为红色时，则出现了父子节点都为红色的情况，性质4被破坏，上面的图就是这个效果。这种情况下，处理会麻烦一些。下面主要介绍这种情况的处理。　

　　既然性质4被破坏，我们就要恢复性质4，恢复的做法只有将父节点变黑，但这样又会引入新的问题，即父节点的路径中黑节点的个数比其它路径多1，那么又需要继续处理，不过我们已经把问题上溯了一层，这样依次解决到根节点，一定可以找到解法，这就是处理核心思想。

　　需要明确一个事实，如果父亲节点为红，则一定有祖父节点，且其颜色为黑。根据其叔叔节点的颜色和新节点的位置，又可以分为如下三种情况：

      a) 叔叔节点为红色，这种情况，不考虑当前节点的位置（左儿子还是右儿子都没有影响）

　　针对于这种情况，除了父节点外，我们可以把叔叔节点一起变黑，但这样叔叔节点和父亲节点路径中的黑节点就比其它路径多1了，因此我们继续把祖父节点变红。这样操作之后，由祖父节点引出的两个路径的黑节点个数没有变化，则其两个子树已经是红黑树了。

　　但是祖父节点变红后，如果祖父的父亲也是红色，则还是破坏了性质4，所以我们需要将祖父节点作为新的当前节点继续由算法来处理。

　　对上图的情况做变化处理，如下：

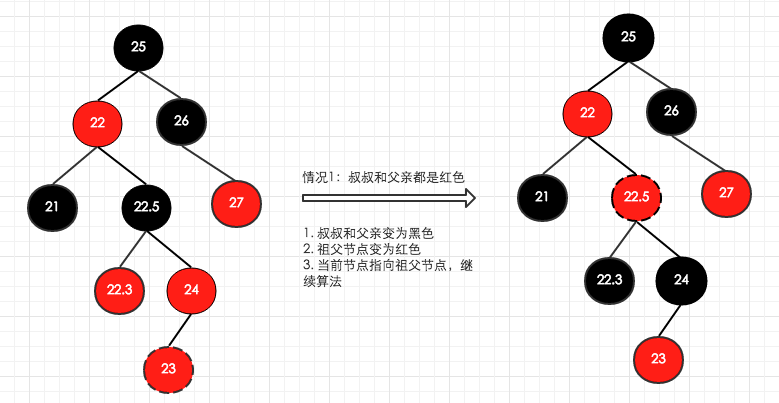
　　b) 叔叔节点为黑色，且当前节点为父亲节点的右孩子。

　　这种情况如上图所示，由于叔叔节点已经为黑色了，所以不能再按上一种方式来处理，这样祖父节点如果还要变红的话，则叔叔节点所在的路径的黑节点的个数就会少1，不满足红黑树了。

      但父节点还是要变黑的，这样就间接说明祖父节点还是要变红，为了达到这一目的，又不影响叔叔节点，有一个完美的解决方案，就是旋转。在上图中，以祖父节点作为支点进行右旋，这样父亲节点升上去，祖父节点成为父亲节点的子节点，这样父亲节点可以变黑，祖父节点变红，叔叔节点上的路径的黑节点的个数一增一减，总个数并没有发生变化。

　　这种想法是可以的，但是在上图中，如果直接这样做的话是有问题的，根据右旋的算法，祖父节点25将变红，并成为当前节点22.5的父节点，如此一来，还是会出现父子节点同为红色的情况。所以不能直接旋转。

　　但我们从上图可以看到，节点22.5的两个子节点都是黑色的，所以假设节点22.5在22的位置，则不存在这样的问题。

　　所以，这种情况我们必须要多做一步，就是以其父节点22为支点进行左旋转，由于支点节点和其右孩子都是红色，所以路径的黑节点个数不会发生变化。

　　这个过程的图示如下：

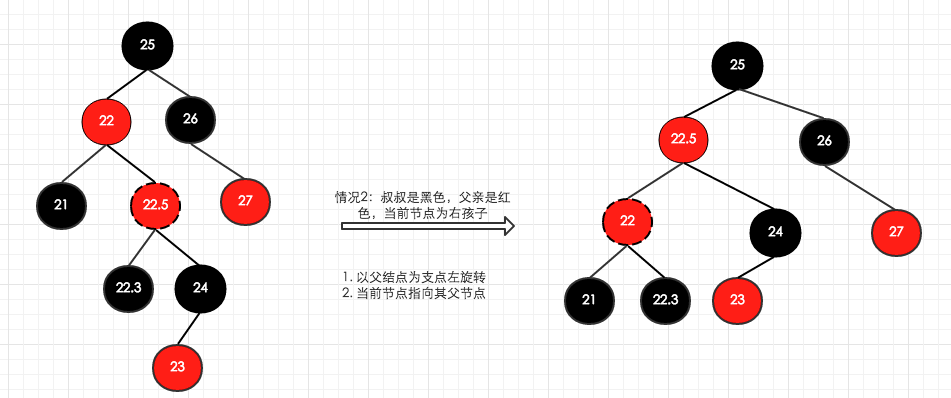
　　需要说明的是一定要让当前节点指向原来的父节点，这样当前节点及其父节点都为红色，才能继续处理，否则，就成了当前节点及其子节点都为红色，无法继续递归了。

　　通过这次旋转，成功的将当前节点是父节点的右孩子的情况，转化为了当前节点是父节点的左孩子的情况。

　　c) 叔叔节点为黑色，且当前节点为父亲节点的左孩子。

　　如果情况2弄明白了，那么这种情况也就比较好理解了，就是通过在祖父节点上右旋，使得父亲节点上移，再将父亲变黑，祖父变红，由于原父亲的右孩子是黑色，所以，祖父节点变红后，其左孩子是黑色，不会破坏性质5.这样整子树就平衡了。示例如下：

　　

　　至此，整个树就算是恢复了红黑树的特点了。

　　需要说明的是，上面的情况2和情况3，都是在当前节点的父节点为祖父的左孩子的情况下来描述的，当父节点为祖父的右孩子时，其处理过程其实是对称的，这里就不再举例了。另外，情况2一定会转成情况3，只是中间多了一个左旋的操作。

　　最后，根节点始终是要置黑的。

　　如果以上都能理解，那么对于任何一种语言的实现包括是伪代码都会很容易理解，下面把JAVA版本的处理代码贴出来，不做详细分析，仅用来说明上述过程的代码描述形式。

private void fixAfterInsertion(Entry<K,V> x) {
        x.color = RED;//新节点为红色

        while (x != null && x != root && x.parent.color == RED) {
            if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
                Entry<K,V> y = rightOf(parentOf(parentOf(x))); //叔叔节点
                if (colorOf(y) == RED) {
                    //叔叔节点为红色的情况
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    x = parentOf(parentOf(x));
                } else {
                    // 为黑色的情况
                    // X为右子树,要多一次左旋转,最终还是要右旋转的
                    if (x == rightOf(parentOf(x))) {
                        x = parentOf(x);
                        rotateLeft(x);
                    }
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateRight(parentOf(parentOf(x)));
                }
            } else {
                //当前节点的父亲为右孩子，操作对称
                Entry<K,V> y = leftOf(parentOf(parentOf(x)));
                if (colorOf(y) == RED) {
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    x = parentOf(parentOf(x));
                } else {
                    if (x == leftOf(parentOf(x))) {
                        x = parentOf(x); 
                        rotateRight(x);
                    }
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateLeft(parentOf(parentOf(x)));
                }
            }
        }
        root.color = BLACK;
    }

 

五、总结

　　红黑树的添加相对来说还是比较简单的，由于新节点都是红节点，所以问题的关键在于，当新节点的父节点是红色的时候，如何消除连续两层红节点的问题。

　　解决问题的中心思想就是想办法将父节点变黑，实现子树为红黑树的目的，这样依次上溯，直到根节点。