从谷歌面试题中反思基础教育人才培养
某天一大早肖同学就拿着一本厚厚的《c++3D游戏编程》书来找我,想要在运动会期间让我开一个机房,他想自学。肖同学一向对编程很感兴趣。但是这次被我一口拒绝了,我随手一翻,就是矩阵运算、欧拉公式等等,好高骛远不行,必须要脚踏地,一步步来,高三了当然必须要先进一个211再说。必须要有良好的数学素养、扎实的语言功底、一流的沟通能力与好的思维品质。
如何面向未来10年培养人,因个人水平非常有限。我们通过一道题一起来看看,全球500强的企业需要我们培养什么样的人才。
一、背景
谷歌是全球最大的IT公司之一,一直通过不拘一格的方式来解决一些问题。2004年的招聘题居然在101号公路的广告牌上,101号公路是硅谷的动脉,因为这条路边全部是大家耳熟能详的各种科技巨头,2004年那时候的巨头包括Adobe,微软,思科,甲骨文,Yahoo,eBay,太阳微电脑等等。

我们一起来看看霸气十足的招聘第一关的题目吧?谷歌2004年的年薪当时在20-100万美金。这是第一关,有趣、霸气、灵感十足。

翻译一下:{e的连续数字中最先出现的10位质数}.com,拿中国人的思维来说太张扬了,但可以看出谷歌求贤若渴,有趣,创意的做事方式,解出这道题才能登录网站。该题目上过时代周刊。
二、大素数的判定
有时候我们想快速的知道一个数是不是素数,而这个数又特别的大导致 O(开根号n ) 的算法不能通过,这时候我们可以对其进行 Miller-Rabin 素数测试,可以大概率测出其是否为素数。
1、两个基本定理
(1)费马小定理:当 p 为质数,有 a^{p-1}Ξ 1(mod , p),不过反过来不一定成立,也就是说,如果 a , p 互质,且 a^{p-1}Ξ 1(mod , p),不能推出 p 是质数。
我们来算两个数试试:
3100 Ξ (mod 17) 用费马小定理: 17为质数,3与17互质,ok, 3100 =316 *316*316*316*316*316*34 由费马小定理可得316Ξ1(mod 17) ∴3100Ξ34 (mod 17) 最终等于13。
第二个:3110 Ξ (mod 17) 3112/32(mod 17)Ξ1/32(mod 17) 这里的1相当于18任何数被17取模余1,18是其中之一。即2为本题结果
(2)二次探测:如果 是一个素数,0<x<p, 则方程x2Ξ1(mod p)的解为x=1 或 x=p-1
证明:x2Ξ1(mod p) => x2-1Ξ0(mod p) =>(x+1)(x-1)Ξ0(mod p) =>x=1或如果p为质数则x=p-1
证明如下:

2、算法的基本流程
(1)对于偶数和 0,1,2 可以直接判断。
(2)设要测试的数为 x,我们取一个较小的质数 a,设 s,t,满足 2^s.t=x-1(其中 t 是奇数)。
(3)我们先算出 a^t,然后不断地平方并且进行二次探测(进行 s 次),并且还要对X取模。要么等于1,要么等于x-1这两种情况是返回真的,即为质数
(4)最后我们根据费马小定律,如果最后 a^{x-1}≠1(mod , x),则说明 x 为合数。
(5)多次取不同的 a 进行 Miller-Rabin 素数测试,这样可以使正确性更高
注意点:
(1)我们可以多选择几个 a,如果全部通过,那么 x 大概率是质数。
(2)Miller-Rabin 素数测试中,“大概率”意味着概率非常大,基本上可以放心使用。
(3)当 a 取遍小等于 30 的所有素数时,可以证明 int 范围内的数不会出错。
(4)代码中我用的 int 类型,不过实际上 Miller-Rabin 素数测试可以承受更大的范围。
(5)另外,如果是求一个 long long 类型的平方,可能会爆掉,因此有时我们要用“快速积”,不能直接乘。
3、万能的python登场
e='''271828182845904523536028747135266249775724709369995957496696762772407663035354759457138217852516642742746639193200305992181741359662904357290033429526059563073813232862794349076323382988075319525101901157383418793070215408914993488416750'''
e=e.replace("\n","")
n=len(e)
prime=[2,3,5,7,11,13,17,19,23,29]
from random import randrange
def miller_rabin(n, k=10):
if n == 2:
return True
if not n & 1:
return False
def check(a, s, d, n):
x = pow(a, d, n)
if x == 1: #小费马定理结论
return True
for i in range(s - 1):
if x == n - 1:
return True
x = pow(x, 2, n) #再次平方取余
return x == n - 1 #二次探测定理中n-1为一个解,为n-1时为正
s = 0
d = n - 1
while d % 2 == 0: #计算出s测试的次数,2^s*d
d >>= 1
s += 1
for i in range(k):
a = prime[i] #前面十个素质都试过,保证没问题
if not check(a, s, d, n):
return False #如果有一个有问题就全为假
return True
for i in range(0,n-9):
num=int(e[i:i+10])
if miller_rabin(num):
print(str(i)+": "+str(num))
答案是:
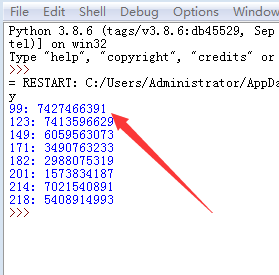
就是7427466391.com
三、回顾
一个问题从开始要解决,需要用到小费尔马定理,通过上述两个小题,定理并不难,从上面可以看出数学基础很重要,但是不死做题,从定理化为代码涉及要语言与基本的数据处理技巧。题目重发现,从另一个侧面可以看出,谷歌招什么样的人?有趣、灵活、对问题乐于钻研、对问题求解着迷、个性张扬的人。首先还是要脚踏实地,如果一群小孩本身学习能力不强,我们还提高考学难度与思维广度,这是对牛弹琴,也无形中制造了差生,大多数学生接受不了的东西,讲了也没意思。其次,对于感兴趣的学生可以点拔点拔,看看其悟性如何,最关键作为老师本身,要脚踏实地刷题,刷题,再刷题,还要不间断的带学生。本人水平有限,认识也不一定到位,相信诸位一定对这道霸气的题有更深入的感想。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号