Github: https://github.com/holidaysss
小组:龙天尧(代码实现),林毓植(浮点转分数函数,代码审查)
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
30 | 30 |
|
· Estimate |
· 估计这个任务需要多少时间 |
30 | 30 |
|
Development |
开发 |
540 | 540 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
60 | 60 |
|
· Design Spec |
· 生成设计文档 |
30 | 30 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
60 | 60 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
30 | 30 |
|
· Design |
· 具体设计 |
120 | 120 |
|
· Coding |
· 具体编码 |
240 | 240 |
|
· Code Review |
· 代码复审 |
60 | 60 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
60 | 60 |
|
Reporting |
报告 |
90 | 90 |
|
· Test Report |
· 测试报告 |
30 | 30 |
|
· Size Measurement |
· 计算工作量 |
30 | 30 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
30 | 30 |
|
合计 |
780 | 780 |
设计实现过程:思路:四则运算题库的功能应该包括 出题,计算答案, 对比答案 这三个主要功能。
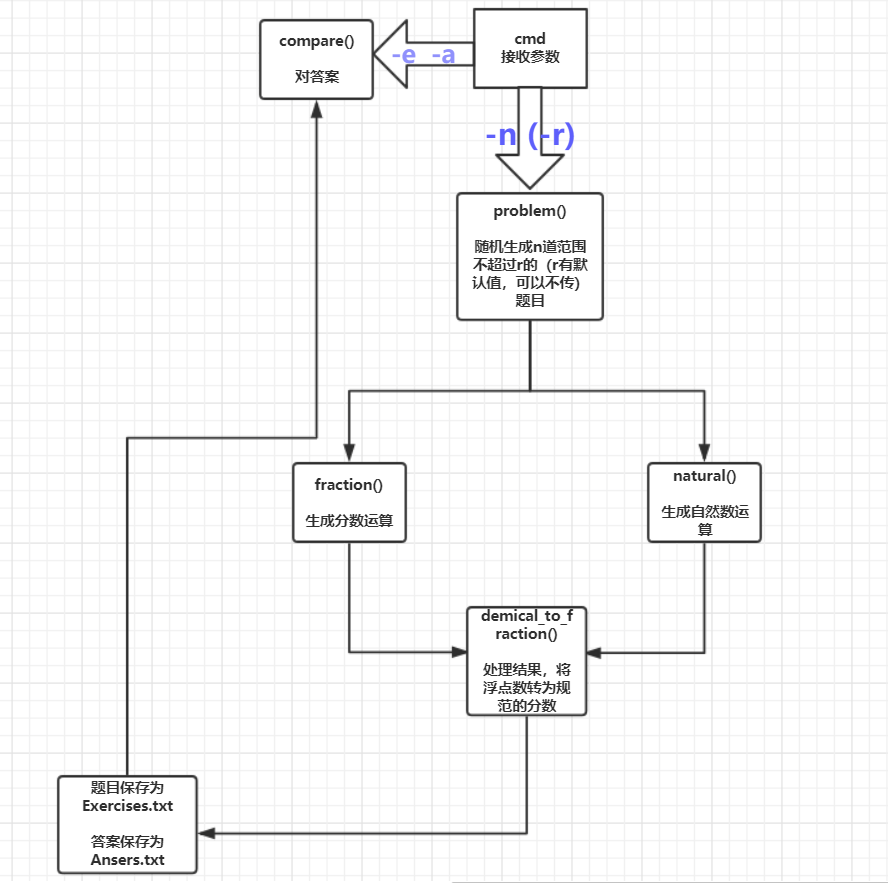
代码说明:
题目生成函数:problem() ,调用natural(),fraction()
def problem(area=10): # 随机生成一道题目(自然数四则运算或分数运算),运算符不超过3个 try: if random.choice([1, 2]) == 1: # 随机生成 自然数或分数 的四则运算 expression, print_expression = natural(area) # 生成一个自然数运算 results = demical_to_fraction(eval(expression)) # 运算结果通过demical_to_fraction()转成分数 else: # 分数四则运算 和上面流程大致相同 expression, print_expression = fraction(area) # 生成一个分数运算 results = demical_to_fraction(eval(expression)) if not results: # 无法转分数 problem(area) return 0 # print_expression_nums = list(filter(str.isdigit, print_expression)) # ['2','+',1'] print_expression_nums = print_expression.replace('(', '').replace(')', '').split() # 将输出表达式拆解 print_expression_nums.sort() # ['+', 1', '2'] if results < 0 or ((str(results)in answers) and (print_expression_nums in str_num)): # 去负答案,去重复 problem(area) else: results = turn_fracrtion(results) # 转化 prints.append(print_expression) answers.append(results) # 答案列表 str_num.append(print_expression_nums) except Exception: # 过滤分母为0的题目 problem(area)
自然数运算生成 natural():
def natural(area): # 生成一个自然数运算 operator_num = random.randint(1, 3) # 随机运算符 expression = print_expression = num = str(random.randint(1, area)) # 第一个数 bracket = (random.choice(['(', '']) if not operator_num == 1 else '') # 非单运算符 可加括号 for i in range(operator_num): # 随机个运算符 op = str(random.choice(operators)) # 随机选择运算符 (+ - * /) if op == '-': # 若为'-',生成数字小于前一个数字 num = str(random.randint(1, int(num))) else: num = str(random.randint(1, area)) # 随机数值,不超过area if bracket == ')': # 右括号在数字右边 print_expression += ' ' + change(op) + ' ' + num + bracket # 用于输出的表达式 例:1×2 expression += op + num + bracket # 用于eval()计算的表达式 例:1*2 else: # 左括号在数字左边 print_expression += ' ' + change(op) + ' ' + bracket + num expression += op + bracket + num bracket = (')' if bracket == '(' else '') # 左括号配右括号, 空配空 return expression, print_expression
分数运算生成 fraction(), gen_fraction():
def gen_fraciton(area): # 生成一个规范分数 while True: a = random.randint(1, area) b = random.randint(1, area) if '/' in str(Fraction(a, b)): return Fraction(a, b) def fraction(area): # 生成一个分数运算 operator_num = random.randint(1, 3) # 随机运算符 num = gen_fraciton(area) expression = print_expression = str(num) # 第一个分数 bracket = (random.choice(['(', '']) if operator_num != 1 else '') # 超过一个运算符才需要加括号 for i in range(operator_num): op = str(random.choice(operators)) if op == '-': # 若为'-',生成分数小于等于前一个分数 while True: next_num = gen_fraciton(area) if next_num <= num: break num = next_num else: num = gen_fraciton(area) if bracket == ')': if float(num) > 1: # 假分数转带分数 例:8/3 -> 2'2/3 print_expression += ' ' + change(op) + ' ' + turn_fracrtion(num) + bracket else: print_expression += ' ' + change(op) + ' ' + str(num) + bracket expression += op + str(num) + bracket else: if float(num) >= 1: print_expression += ' ' + change(op) + ' ' + bracket + turn_fracrtion(num) else: print_expression += ' ' + change(op) + ' ' + bracket + str(num) expression += op + bracket + str(num) bracket = (')' if bracket == '(' else '') # 左括号配右括号 return expression, print_expression
假分数转化函数 turn_fraction():
def turn_fracrtion(results): # 假分数转带分数 if isinstance(eval(str(results)), int) or (eval(str(results)) < 1): # 整数和真分数 return str(results) else: return str(int(results)) + "'" + str(results - int(results)) # 假分数
符号转化函数 change():
def change(a): # *,/ 转成 ×,÷ if a == '*': a = '×' elif a == '/': a = '÷' return a
eval函数处理的结果出来是浮点数,不符合要求,苦想不解,让毓植写了个浮点转化分数的函数:
def find_cycle(demical): # 找小数的循环体(参数为小数部分) for i in range(1, 17): cycle_part = demical[:i] # 截取小数部分的前i位,假设为循环体 if len(cycle_part) < 4: # 如果循环体较短 if (cycle_part*3) == demical[:3*i]: # 需要满足4次重复 return cycle_part # 满足才认定为循环体 else: # 如果循环体较长 if (cycle_part*2) == demical[:2*i]: # 满足2次重复 return cycle_part return 0 # 找不到循环体,返回0 def demical_to_fraction(n, zero_num=0): # 小数转化分数 n = str(n) # 规范输入为字符串形式 if len(n) < 16: # 如果是有限小数,直接返回 return Fraction(n) real_num, dot_area = n.split('.') # 获取整数 和 小数 float_num = float(n) # 转化一个浮点数用于计算 for i in range(len(n)): cycle_start = dot_area[i:] # 从第i位开始,开始截取字符串 result = find_cycle(cycle_start) # 从截取的字符串中找到循环体 length = len(str(result)) # 判断循环体的长度 if result: # 如果存在循环体 if i != 0: # 如果循环体的开始不是小数点后第一位 eg 0.13888888 new_number = float_num*(10**i) # 移位数使循环体是小数点后的开始 eg 13.8888 demical_to_fraction(new_number, i) # 将新生成的数递归使用 break else: # 如果循环体直接在小数点后的第一位 fraction = Fraction(int(result), int('9'*length)) # 小数部分转化为分数 /数学知识需要了解 final_num = int(real_num) + fraction # 小数点前的部分需要从重新加上 return final_num/(10**zero_num) # 回退移的位数
以上是主要函数
具体源码后面会上传到github
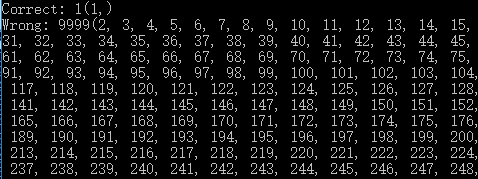
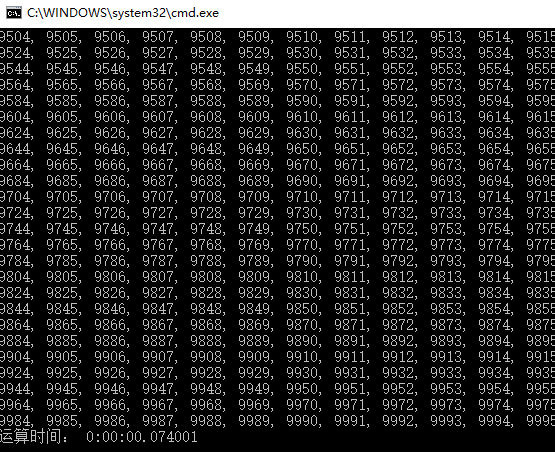
运行结果:
生成一万道题:


小学生就可以在记事本上做题啦
一年后。。
感觉良好
开始对答案

还行

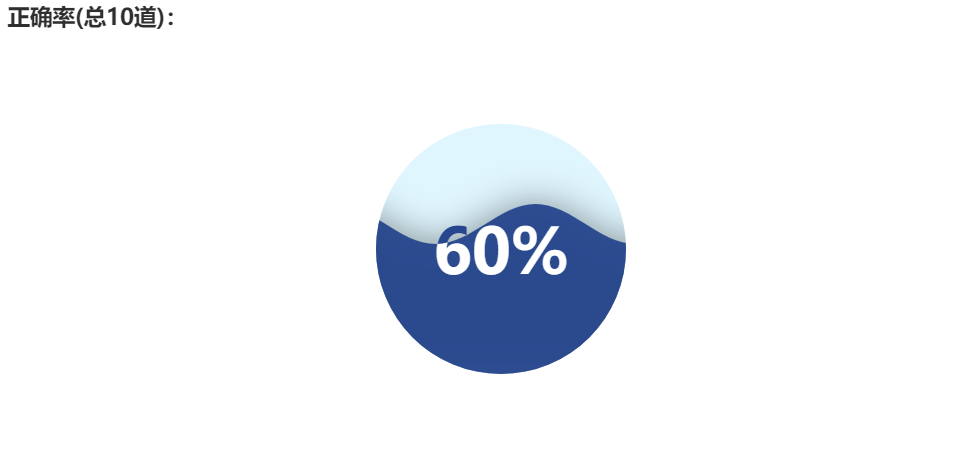
为了方便家长了解学生的成绩, 在 答案对比 处增加了水型球比例图。(具体代码Github已更新,这里就不修改了)
好了。。。
问题记录:1.出现了溢出错误,发现是条件判断的问题,已修改。 2.优化逻辑,分解problem()函数。 3.修改去重逻辑,优化程序运行速度. 4.拓展对比答案功能,增加水型球比例图。 5.需求看错了,过程不能出现负数看出结果不出现负数, 已修改。
6. 忘记吧结果的假分数转化了。。已补上。 7.日常优化。。。。。。。。 8.优化答案对比 ( 最后一次改了,再改我
项目小结:这个项目挺有意思的,主要运用到”随机性“,小逻辑特别多,主要思路还是有迹可循的,继续努力,加油。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号