cFSMN和FSMN参数规模对比分析
1. FSMN参数规模分析
(1)分析前提：
- 假设隐藏层单元规模都为n
- 只分析前向t个时刻的结构，即暂时不考虑双向的结构
- 只分析向量系数编码，即vFSMN，暂时不考虑sFSMN
(2)结构图回顾：
(3)公式回顾：
\[\vec{\tilde{h}_t^l} = \sum_{i=0}^{N}\vec{a_i^l}\odot\vec{h_{t-i}^l},in...vFSMN
\]
\[A^l =\{ \vec{a_0^l},\vec{a_1^l},...,\vec{a_N^l}\},in...vFSMN
\]
\[\vec{h_t^{l+1}} =f(W^l\vec{h_t^l}+\tilde{W}^l\vec{\tilde{h}_t^l} +\vec{b^l} )
\]
(4)参数规模分析
由第一个公式和第二个，可知这一部分的参数规模为：n × t
由第三个公式，可知这一部分的参数规模为：n × n + n × n
所以总的参数规模为：n × n + n × n + n × t
2. cFSMN参数规模分析
(1)分析前提：
- 与FSMN的分析前提完全一致
- 假设投影层的投影矩阵是x × n维的
(2)结构图回顾：
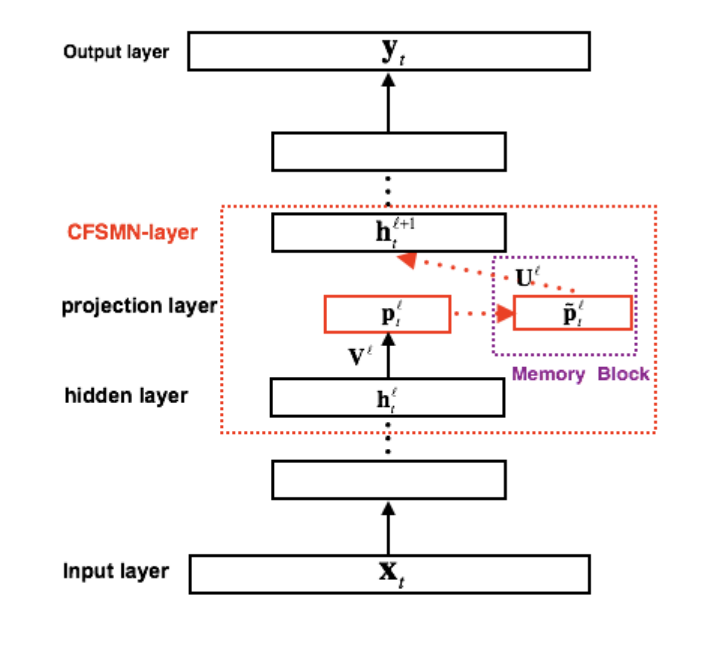
(3)公式回顾：
\[\vec{p_t^l} =V^l\vec{h_t^l}+\vec{b^l}
\]
\[\vec{\tilde{p}_t^l} = \vec{p_t^l}+\sum_{i=0}^{N}\vec{a_i^l}\odot \vec{p_{t-i}^l}
\]
\[\vec{h_t^{l+1}} =f(U^l\vec{\tilde{p}_t^l} +\vec{b^l} )
\]
(4)参数规模分析
由第一个公式和假设，可知这一部分的参数规模为：x × n
由第二个公式，可知这一部分的参数规模为：x × t
由第三个公式，可知这一部分的参数规模为：x × n
所以总的参数规模为：n × x + n × x+ x × t
3. 对比
FSMN的参数规模为：n × n + n × n + n × t
cFSMN的参数规模为：n × x + n × x+ x × t
所以：cFSMN相比于FSMN，减少的参数规模为： (2n+t) × (n-x)
进一步的，实际上n很大，可以忽略t的影响，所以上式可以近似为：2n × (n-x)
可以看到，如果取x为n的一半，较少的参数规模就是n2
近似分析的结果，就是参数规模可以减少的量级为：O(n2)
