算法-动态规划(DP)
时间:2022/09/21
一. 引入-斐波那契数列
下图展示了斐波那契数列数列的递归式:
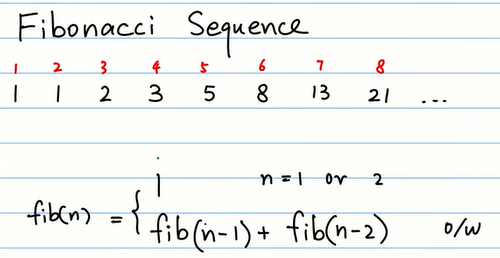
然后我们再看一下在计算fib(7)的时候会出现什么问题:
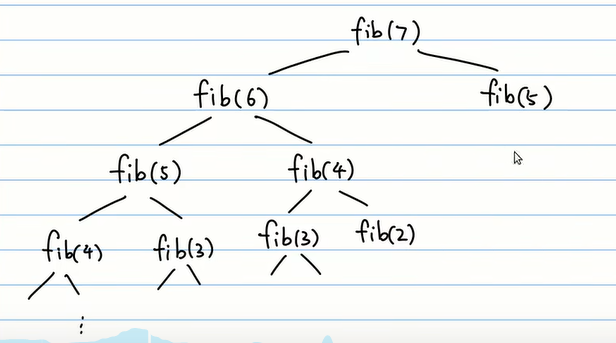
如上图所示,在计算fib(7)的时候,它会计算fib(6)和fib(5),然后在计算fib(6)的时候又会把fib(5)再计算一遍,这就会出现重复计算的问题(重叠子问题),导致算法的时间复杂度为O(2n)。
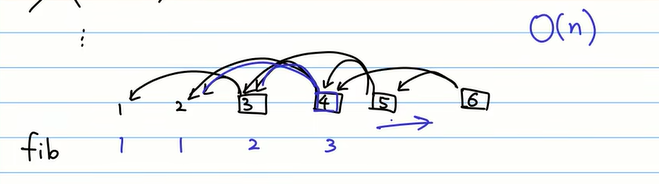
对于上面这个问题,比较好的方法在计算出左边的fib(5)之后就把该值存起来,当右边再次用到fib(5)的时候就把该值直接取出来,不用再次计算。即当计算中存在很多重叠子问题时,把重叠子问题的值存放起来,用到的时候再取出来。如果用这种思想,可以从头进行计算并保存结果,此时的时间复杂度为O(n),如下图所示:
2. 计算最大值问题
2.1 例1
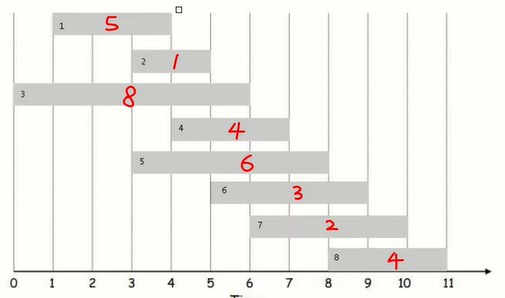
题目描述:现在你有8个任务,每个任务上红色的数字表示这个任务的收益,除此之外,每个任务还有自己的开始时间和截至时间,在同一段时间内只能一项任务,现在需要计算可以赚的最多的钱数:
对于这类问题,可以使用选和不选的方法来写递归式,设OPT(i)表示当考虑第1,...,i个任务时,最优解是什么。以OPT(8)为例,其考虑的是第1,...,8个任务时的最优解,这时就包含两个情况,分别是选第8个任务和不选第8个任务,当选第8个任务时,第8个任务本身的收益是4,而且选完第8个任务之后,再往前要从第5个任务开始,所以选择第8个任务时的结果为4+OPT(5),当不选第8个任务时,它的结果就是简单的OPT(7)。
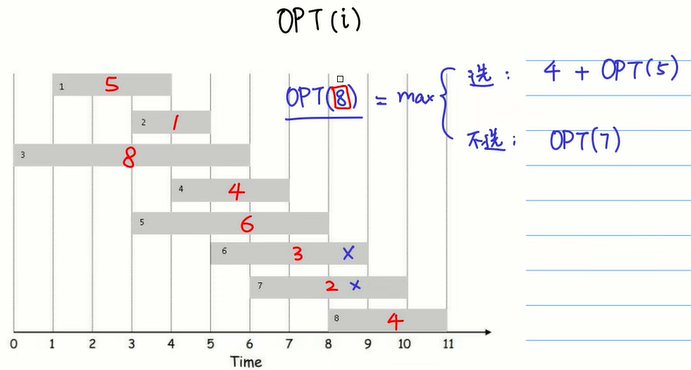
最后得到的递归式如下图所示,这里的prev(i)表示当选择i时,它之前能选择的任务编号:

我们接下来通过画递归树来看一下这个题目是否有与斐波那契数列数列相同的问题:
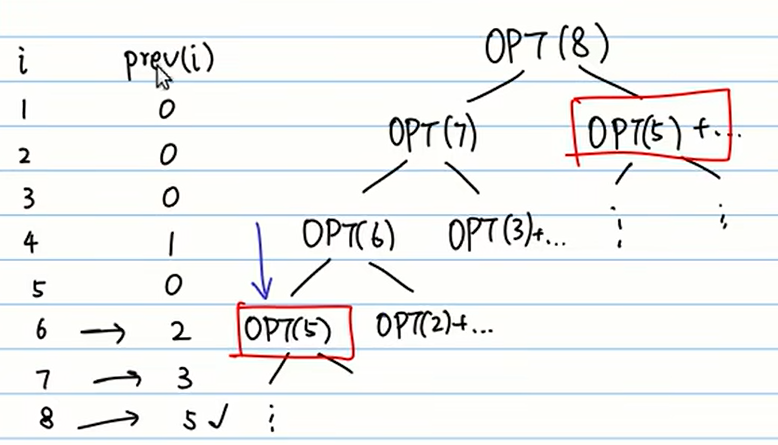
从上图中可以看出,如果按照给出的递归式进行计算,那OPT(5)也被计算了两次,即存在重叠子问题。
所以这道题在做的时候也和斐波那契数列的计算过程一样,通过数组来保存已经计算过的值,从头开始向后计算。
这里引入了一个数组OPT,并从i=1开始(这里为了方便和任务对应是从1开始的),一直计算到i=8,最后的OPT(8)即是所能赚到的最多钱数:

2.2 例2
题目描述:从下列数字中选出一组数字,要求这组数字不能是相邻的数字,并且这组数字的和是最大的。

如上一个题目那样,这里先将问题进行阶段划分,如下图所示,OPT(6)表示到下标为6的位置的最佳方案。
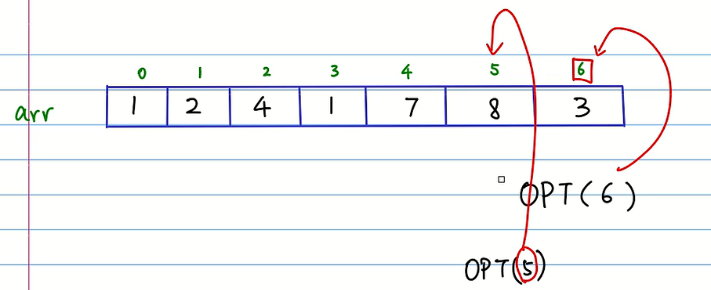
在划分完不同阶段之后,需要找不同阶段之间的关系:
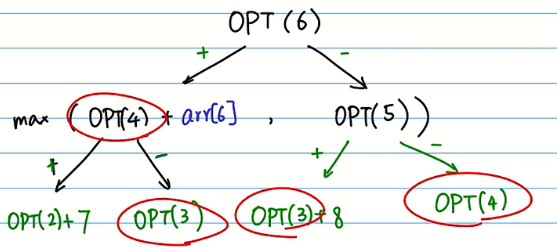
从上图可以看出,这个问题的递归树中也存在重叠子问题。
可以根据阶段之间的关系来写出递归式:

在写出递归式之后就要找递归的出口:
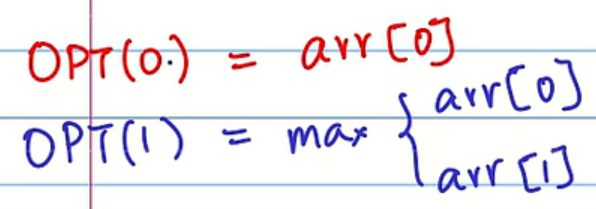
3. 计算特定值问题
题目描述:判断是否能从下面一组数字中选出一些数,使其和正好等于给定的值S,如果存在则返回true,否则返回false。
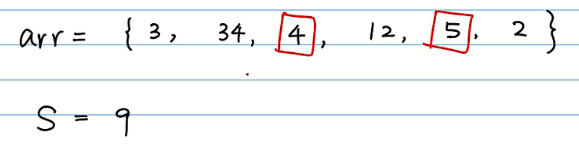
首先也是分阶段,构造subset(i,s)表示考虑前i个数字,能否选出一组数使其正好等于s。
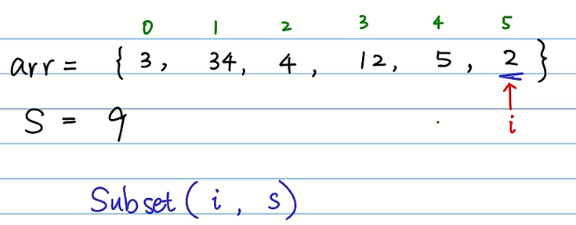
阶段划分完成之后需要找各个阶段之间的关系,这里也是一个选和不选的问题。
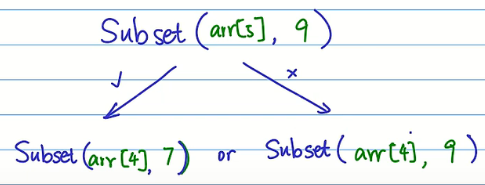
在通过递归树找到各个阶段之间的关系之后,就可以写出该问题的递归式。
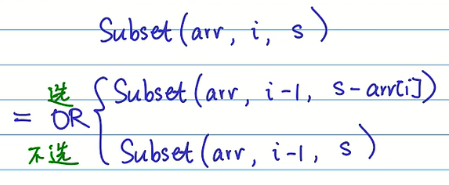
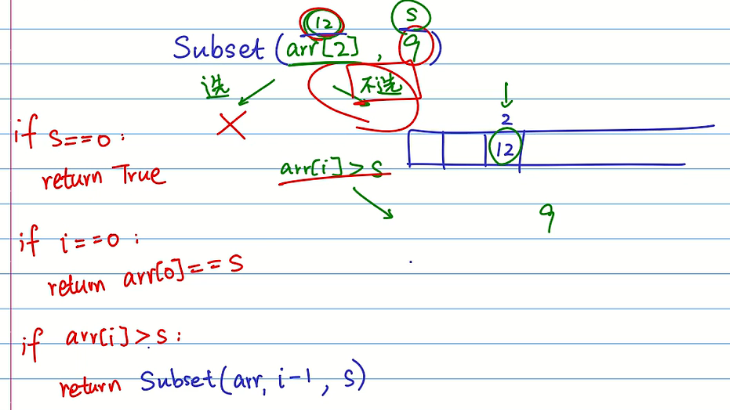
写完递归式之后不要忘记找递归的出口。
最后可以将递归的方法通过数组转化为非递归的方法:
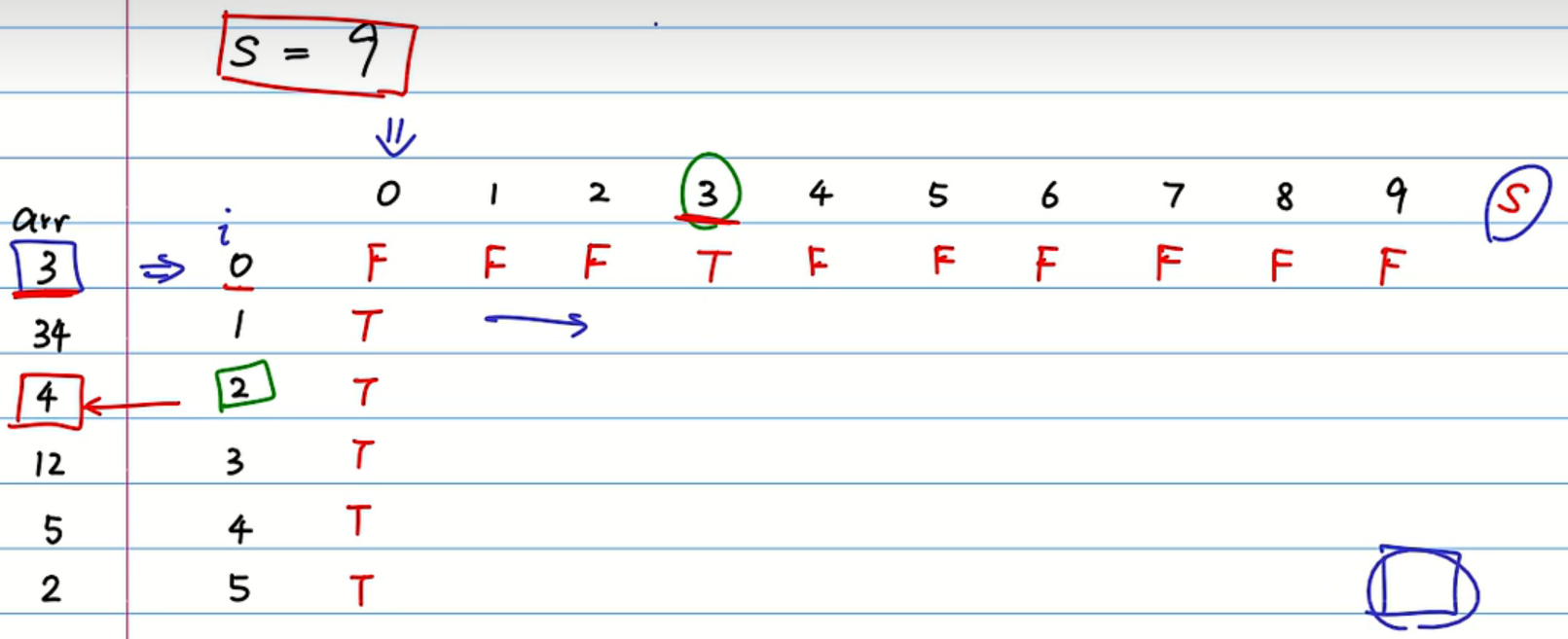
这里使用的是一个二维数组,在使用非递归的方法来解决动态规划问题时,不要忘记将数组的边界填上。
4. 总结
动态规划问题可以分为
1)划分阶段
2)通过递归树寻找阶段之间的关系
3)根据阶段之间的关系写出递归式
4)找出递归式的出口
5)通过数组转化为非递归方法
参考:
1. https://www.bilibili.com/video/BV12W411v7rd/?spm_id_from=autoNext&vd_source=dd301934ea958149e300968ba21afd5d


