改善深层神经网络:超参数调试、正则化以及优化课程笔记-吴恩达深度学习课程第二课(更新中。。。。)
时间:2021/02/04
一.深度学习的实用层面
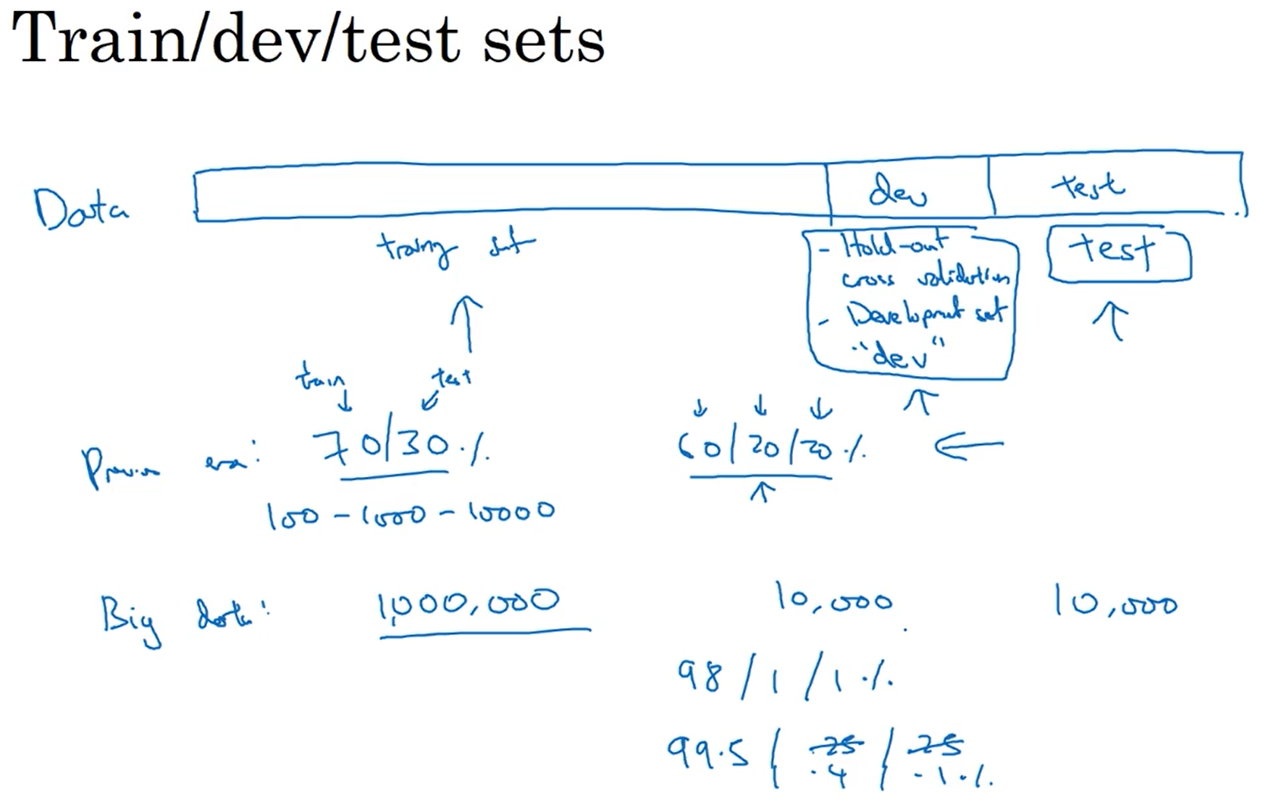
1.1训练_开发_测试集
对于训练数据(在监督学习的情况下,训练数据既有输入值x,又有输出值y),通常会将数据划分为训练集、验证集和测试集。训练集的作用是对模型进行训练,优化参数;验证集用来选择最好的模型;测试集用来对选择的模型进行评估,无偏评估算法的运行状况。在有大量数据的情况下,验证集和测试集的比例一般比较低。有的时候没有测试集也可以。(如果一个神经网络可以由不同的算法实现,首先对于每个算法在训练集上进行训练,然后对于所有算法在验证集上进行验证,选出效果最好的算法模型,最后在测试集上无偏评估选出来的这个算法)
1.2偏差_方差
方差variance:方差高对应过拟合;偏差bias:偏差高对应欠拟合。
如下图,当训练集误差低,验证集的误差高时,说明对数据过拟合,此时高方差;当训练集误差高,验证集误差与训练集相近时,对数据欠拟合,此时高偏差;当训练集误差高,验证集的误差比训练集还要高不少时,高方差且高偏差;当训练集和验证集的误差都比较低时,低方差且低偏差。上述结论都是在基本误差比较低的情况下成立,也就是说判断训练集误差是否高的标准是基本误差,而判断验证集误差是否高的标准是训练集误差。

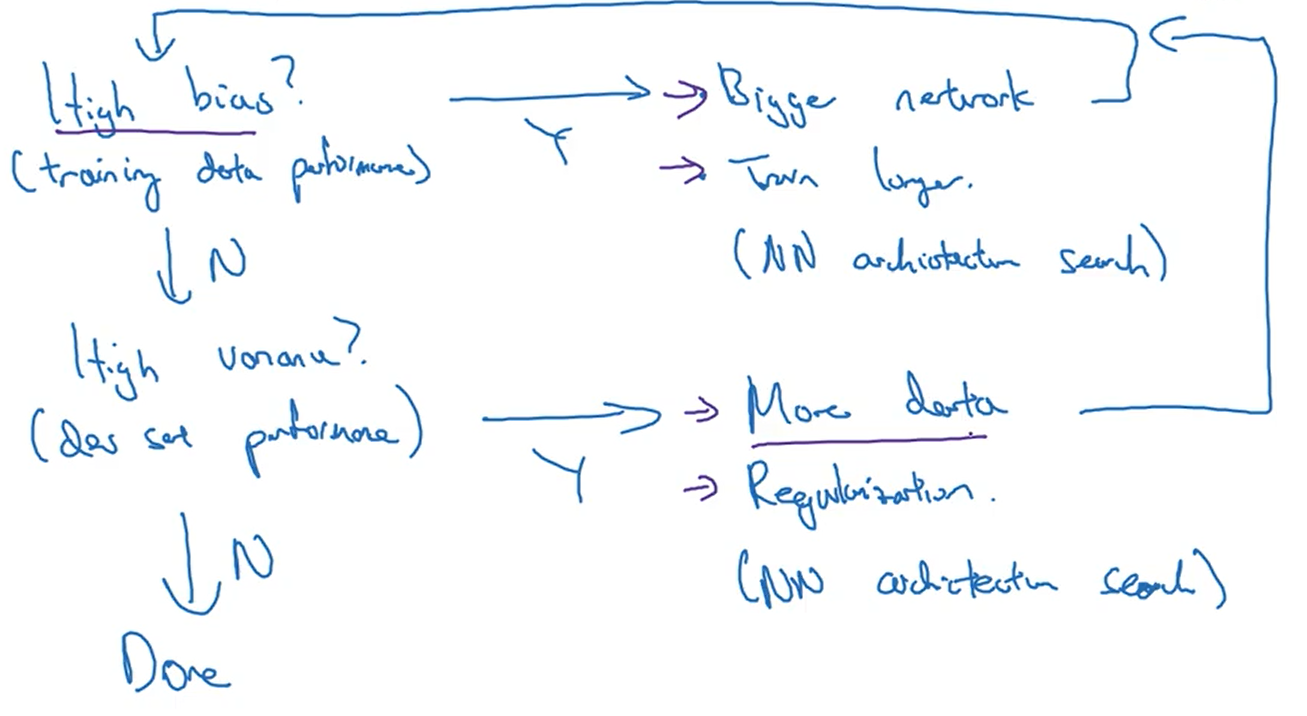
1.3机器学习基础
当我们构建一个神经网络时,我们通常会通过训练集和验证集判断偏差的大小,因为我们至少要保证该神经网络可以对数据进行拟合,这是最低要求。当偏差过大时,我们通常使用更大的神经网络、更多的数据进行训练以及其他的神经网络框架来减少偏差。当偏差到达可以接受的范围时,然后判断方差的大小,如果方差过大,可以通过使用更多的数据、正则化以及其他的神经网络框架来减少方差的大小。
1.4正则化
正则化也就是在成本函数的后面再加了一项,下图列出了L1正则化和L2正则化的公式,在深度学习中我们通常使用L2正则化,也就是参数w各项的平方和。因为参数w几乎涵盖所有的参数,所以这里我们在正则化的过程中只是用了参数w,写上参数w也不错。
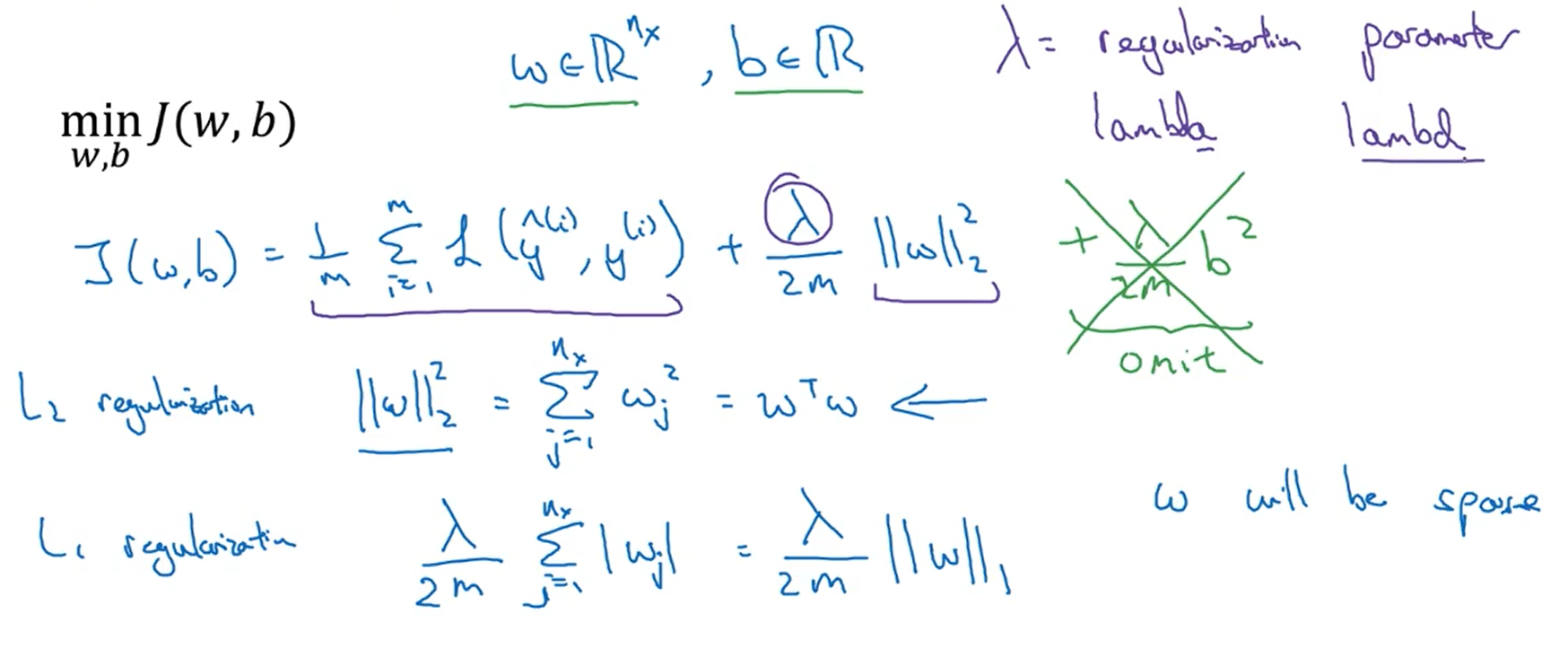
下图推导了正则化之后反向传播求导的公式,正则化其实使w的权重变小了,所以L2正则化也被称为权重衰减。在这个过程中我们引入了一个超参数λ。
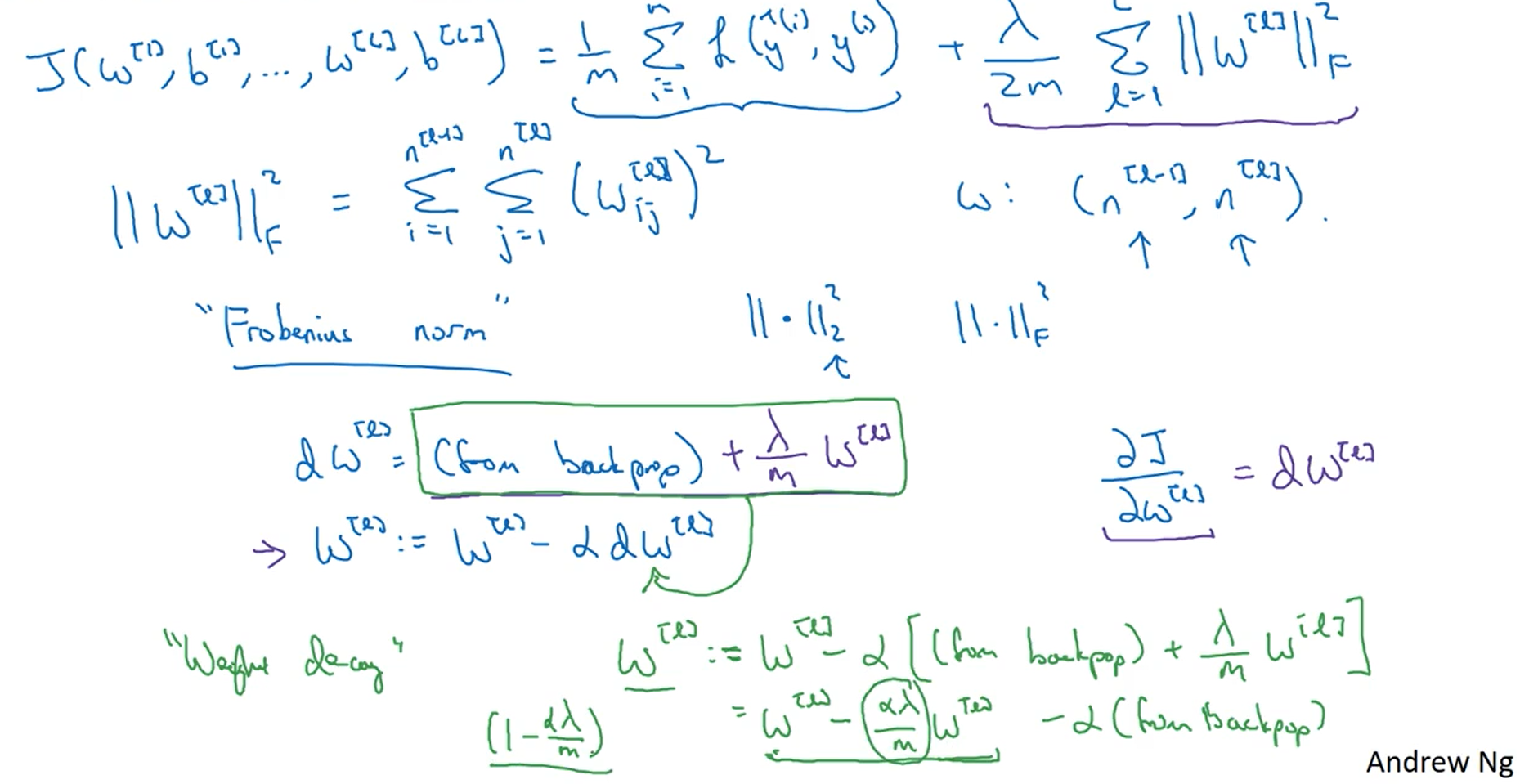
1.5为什么正则化可以减少过拟合
从下图中我们可以看出,假设一种极端情况,即λ取值很大,这样反向传播更新w时会使w的值接近0,w接近0说明很多神经元节点的影响变的很小也就使整个神经网络接近于线性函数,变为了欠拟合的状态。所以存在一个中间状态的λ,使模型从过拟合到正常的状态。
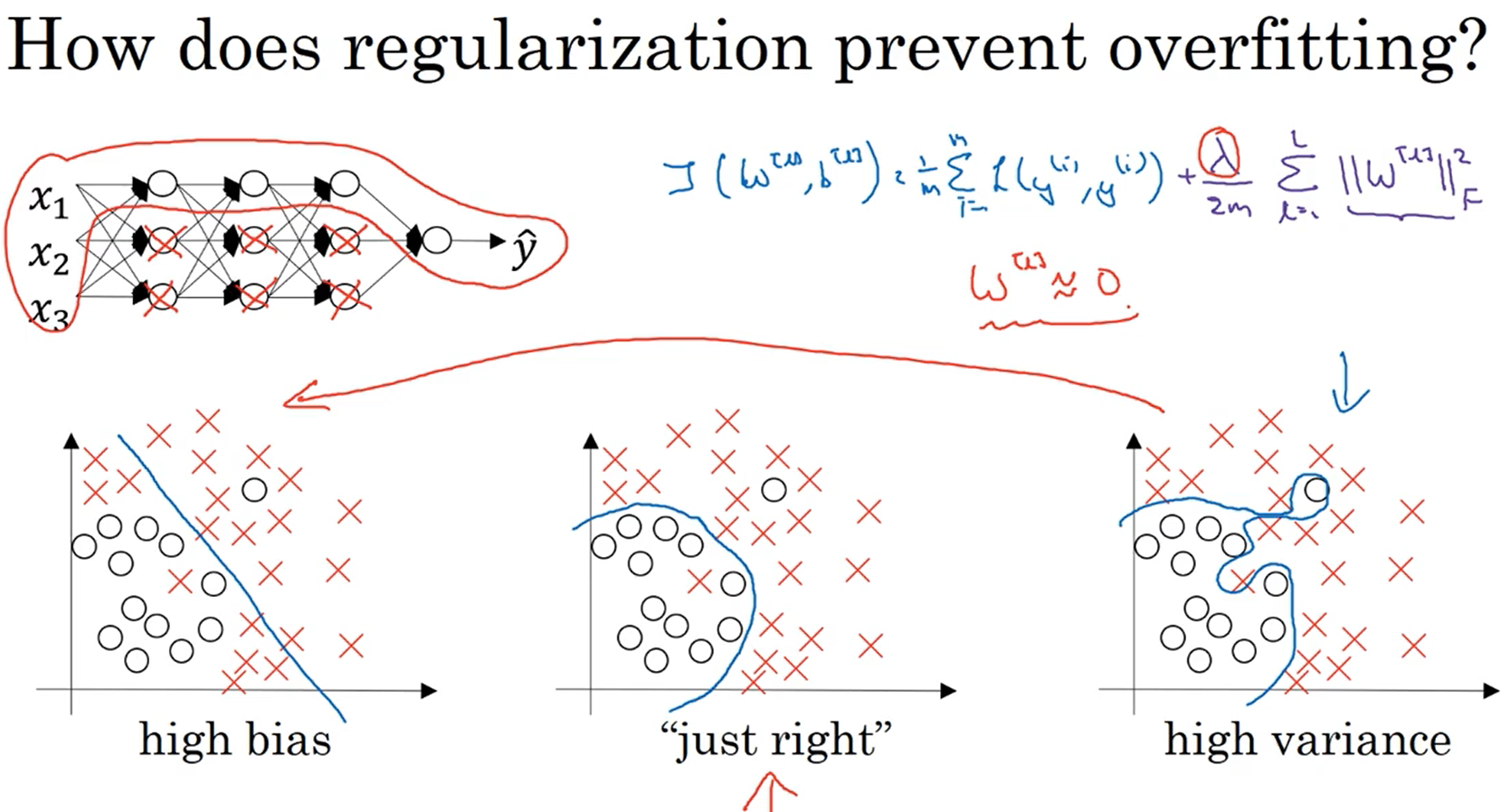
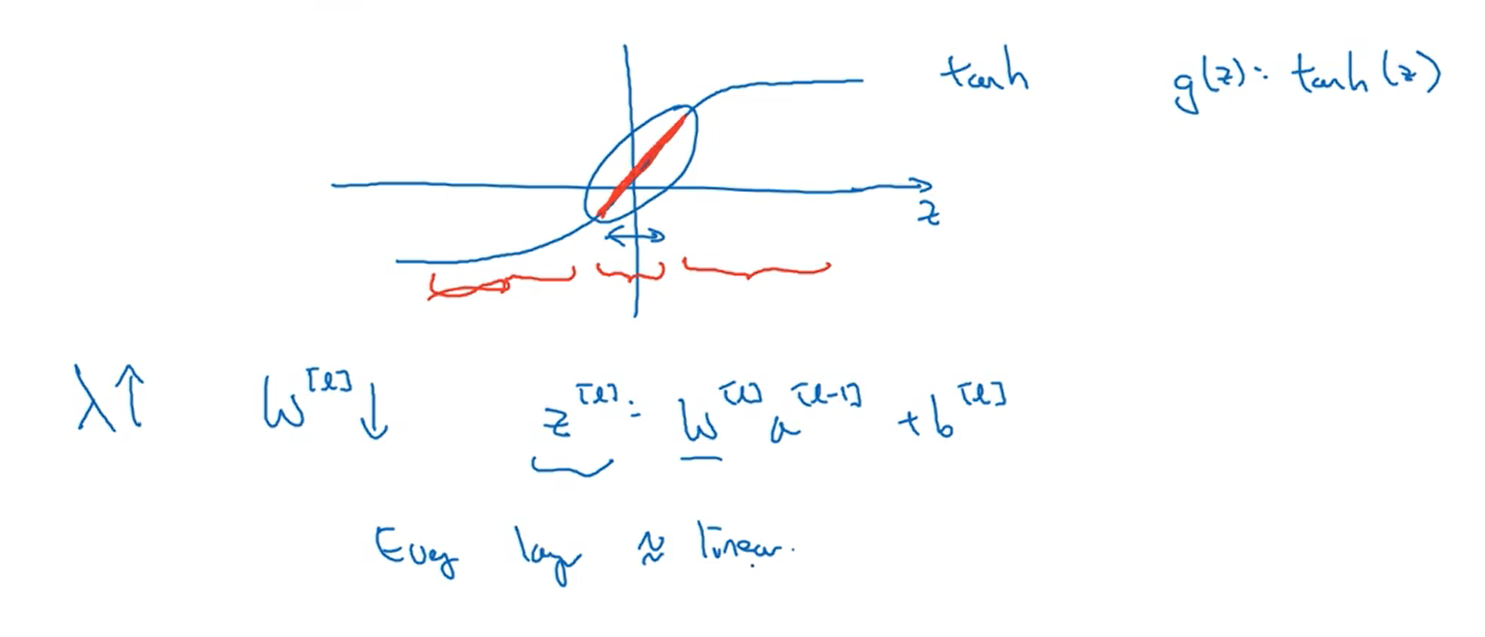
这里假设我们使用的激活函数是tanh,当λ很大时,w接近于0,z也接近于0,此时tanh的曲线接近于线性的,这个神经元节点作为一个线性节点的作用可以忽略。
总结:正则化之所以可以解决过拟合的问题,是因为它使很多神经元节点的作用大大减弱,也就使整个神经网络变的更简单,使它只能拟合相对简单的函数,也就不会出现过拟合的问题。
1.6Dropout正则化
dropout的原理就是对于神经网络的每层设置一个阈值,当该神经节点对应生成的随机数超过这个阈值时,该神经节点以及与它相连的线都会被删除,使神经网络变的节点数更少,更简单,所以能够很好的解决过拟合的问题。
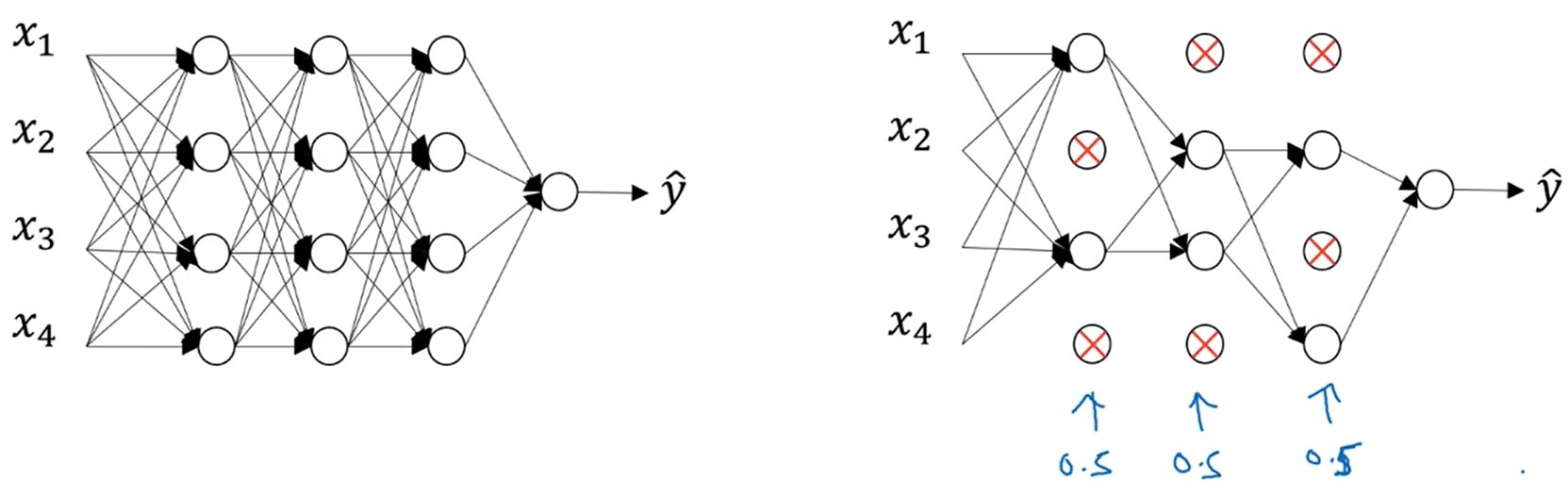
反向随机失活是dropout最常用的实现方法,下图是具体的实现方法:首先设置一个keep-prob,然后生成一个随机矩阵,当矩阵中的值小于keep-prob时为1,即保留,大于时为0,即隐藏该神经节点。然后将该0-1矩阵与对于层的a矩阵相乘,实现隐藏神经单元的效果。将新生成的a矩阵除以keep-prob,这样做的目的是使矩阵a前后的期望保持不变。

1.7理解Dropout
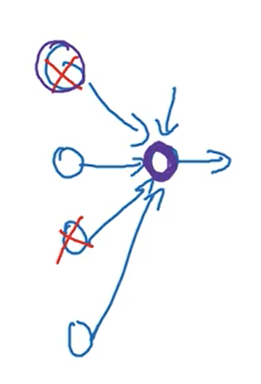
首先dropout类似于正则化,它减少了神经节点的数量,得到了一个更加简单的神经网络,所以可以有效解决过拟合的问题。其次,从下图我们可以从单个神经节点进行理解,在使用dropout之后,由于一个神经节点的几个输入可能会被隐藏,所以不能给其中一个输入很大的权值,所以会使各个输入的权值分散,起到权值衰减的作用。
从下图中可以看出,对于每一层的keep-prob值是可以不同的,对于参数多、容易出现过拟合的层的keep-prob值小,参数少、不容易出现过拟合的层keep-prob值较大。而且dropout经常用于计算机视觉领域。
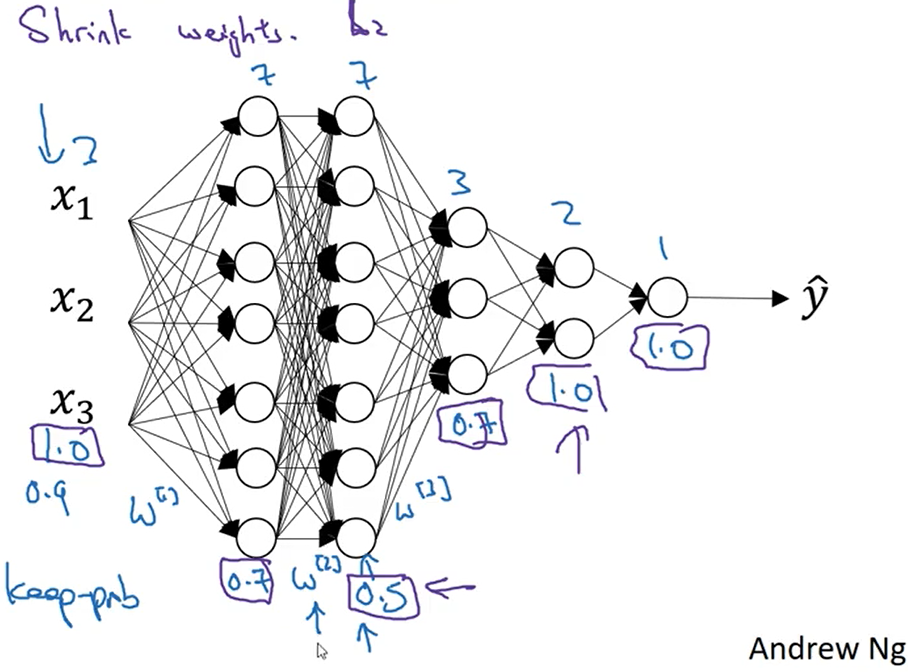
1.8 其他正则化方法
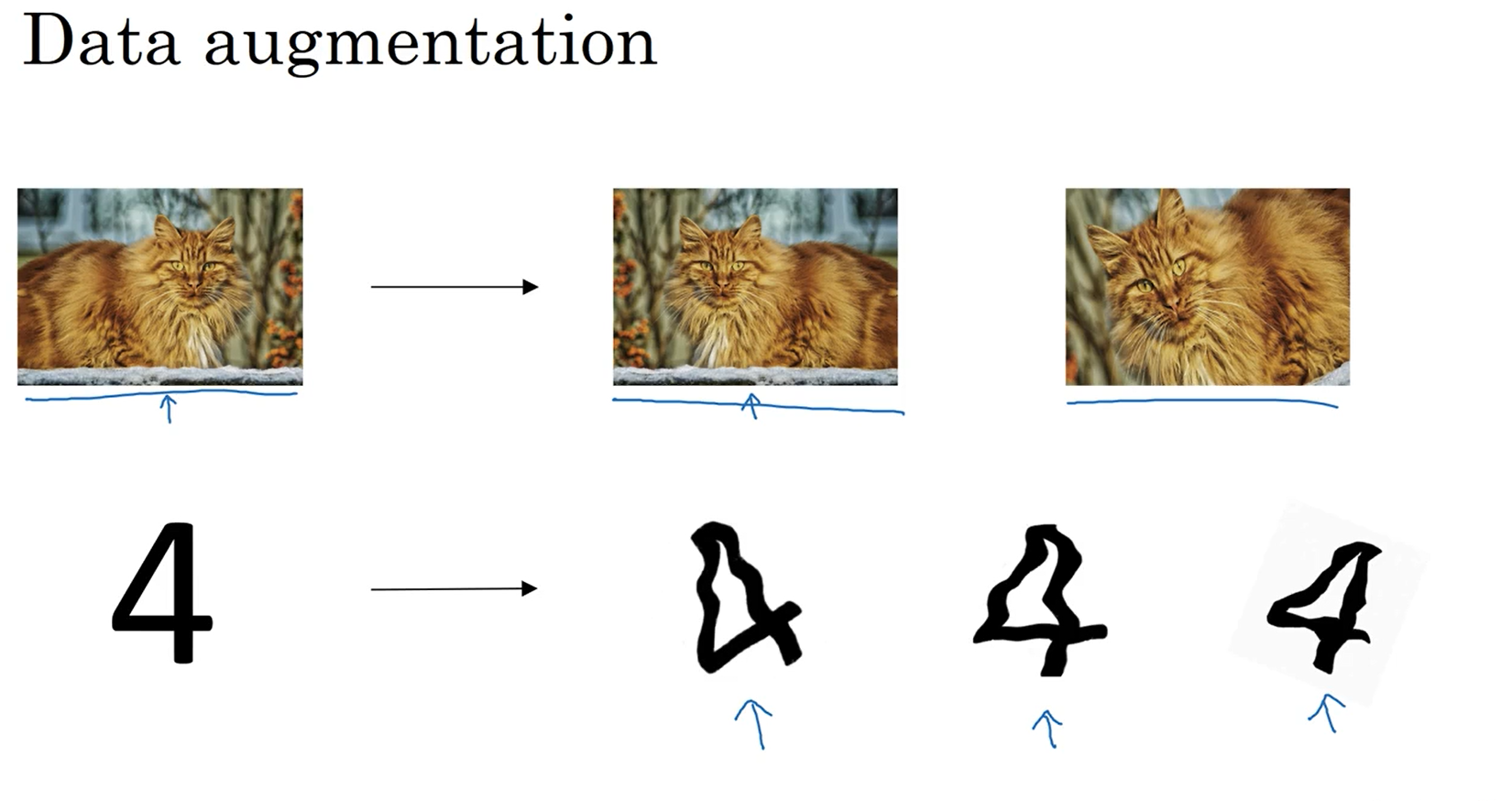
该节主要讲述减少方差的其他方法,首先是数据扩展。对于图像,我们可以进行水平旋转或者旋转后放大截取图中要是别的物体部分,虽然这样做不如加入新的照片,但是代价更小。
第二中预防过拟合的方法是early stop,通常验证集误差开始是下降的,当到达某个点后训练集误差会上升,他的原理就是在训练模型的过程中使成本函数的值递减,当迭代到验证集误差上升时停止迭代。
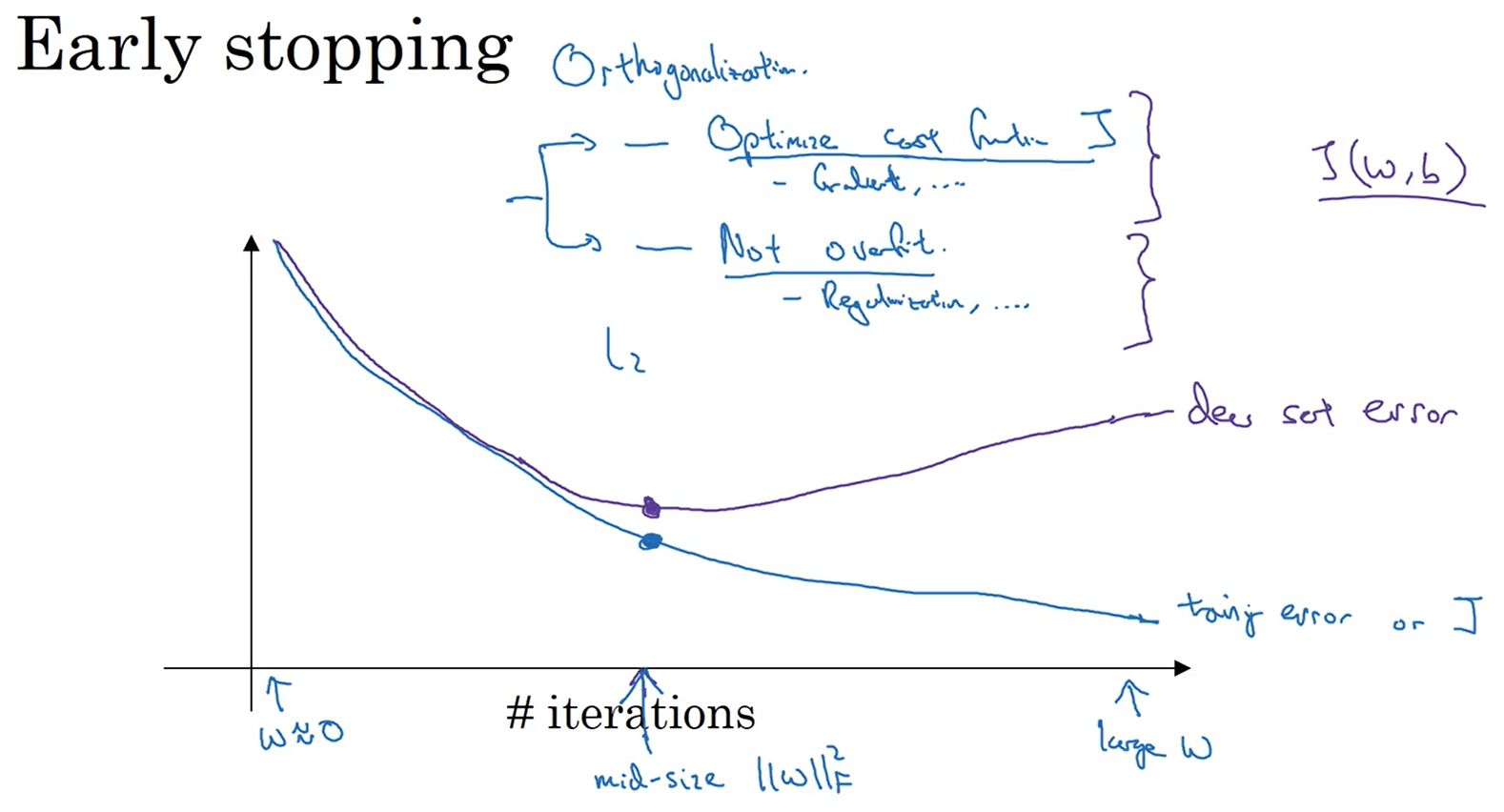
对于early stop方法的缺点:当我们创建一个神经网络时,通常分为两个过程,第一个过程训练神经网络,该过程的目的是使成本函数的值减少;第二个过程使预防过拟合。本来在进行第一个过程时不用考虑第二过程,但是使用early stop时使这两个过程变成了一个,即在保证成本函数下降的过程中不要使方差变的太大。
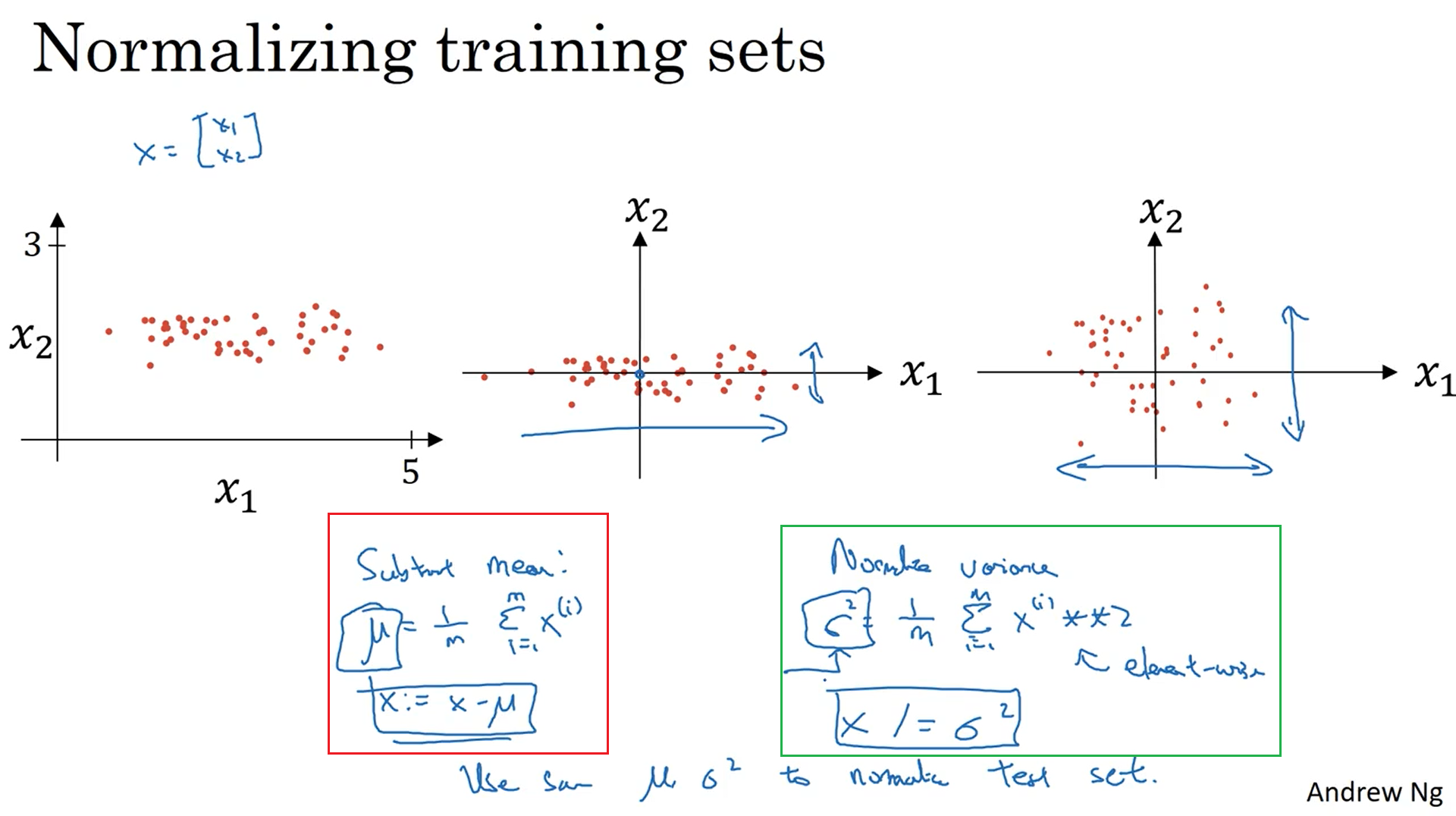
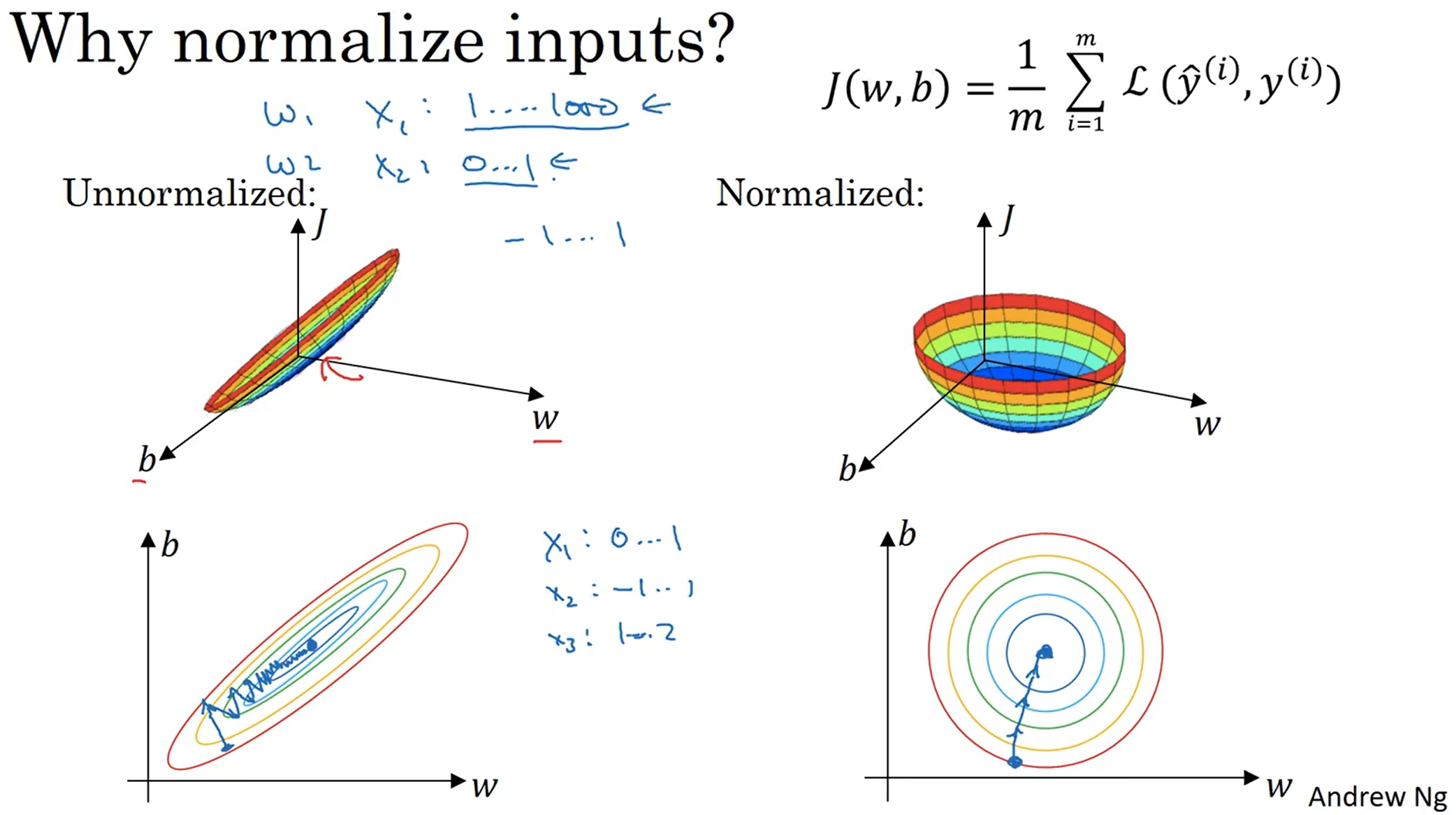
1.9归一化输入
对于两个范围相差较大的输入,我们通常对其进行归一化处理。归一化有两步,第一步是零均值化,也就是下图中红框的部分,首先求出输入特征的均值,然后令x减去均值;第二步是归一方差化,令两个输入特征值的方差都为1。并且当我们通过训练数据求出μ和σ2时,测试集也要使用相同的,即训练集的μ和σ2。
下图解释了我们为什么要归一化输入:根据成本函数的公式,如果我们没有对输入进行归一化,那使用梯度下降时的图像是左边的两个,下降是比较慢的,当进行归一化之后,图像就变味了右边两个,此时梯度下降较快,迭代次数较少,可以提高训练模型的效率。
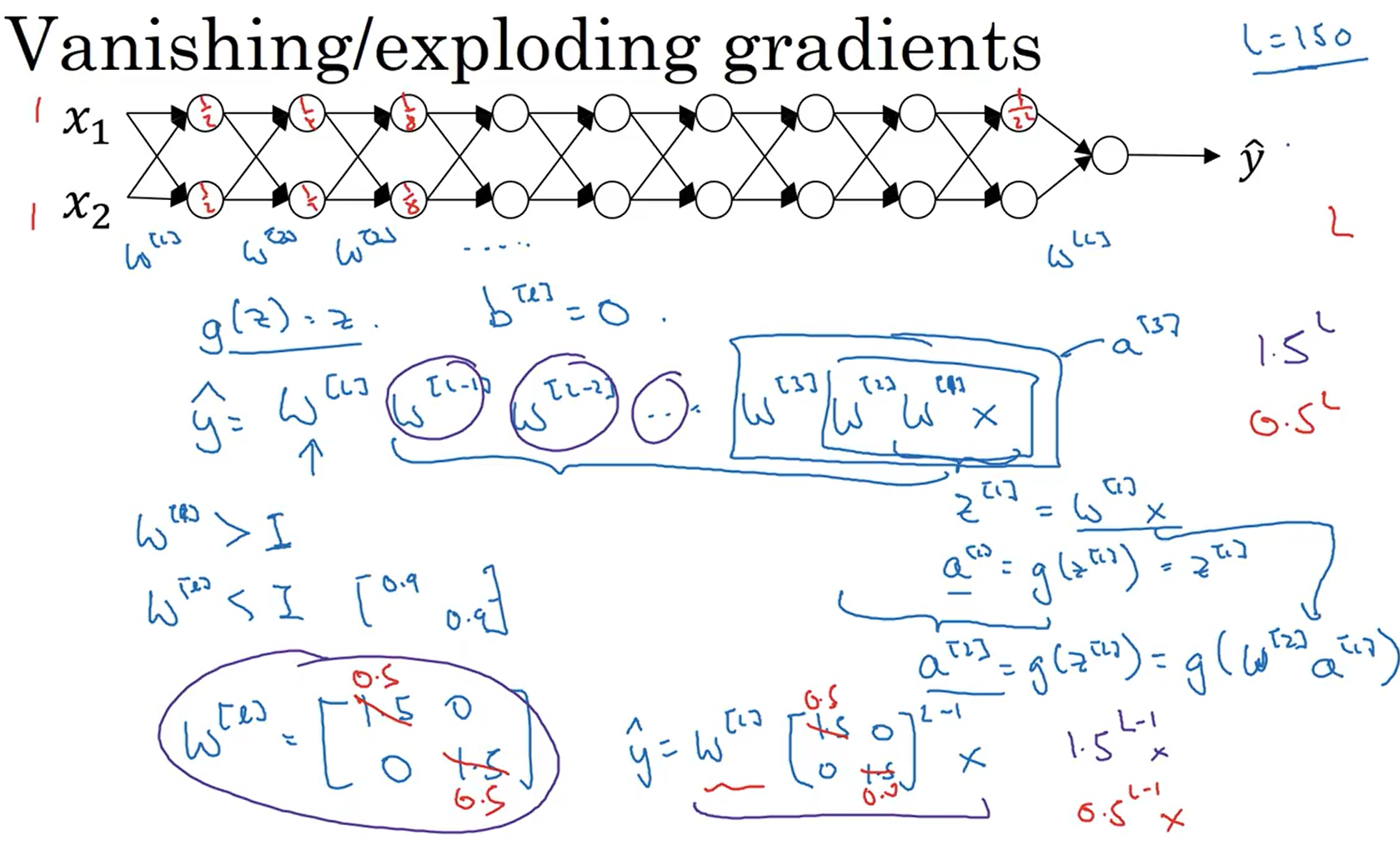
1.10梯度消失与梯度爆炸
如下图一个神经网络,令b=0,激活函数为线性函数,当每一层的参数都为对角矩阵且对角线上都是大于1的数值时就会产生梯度爆炸的问题,因为此时y的值指数增长,当对角矩阵上的数都小于1时就会产生梯度消失的问题,y的值指数下降。
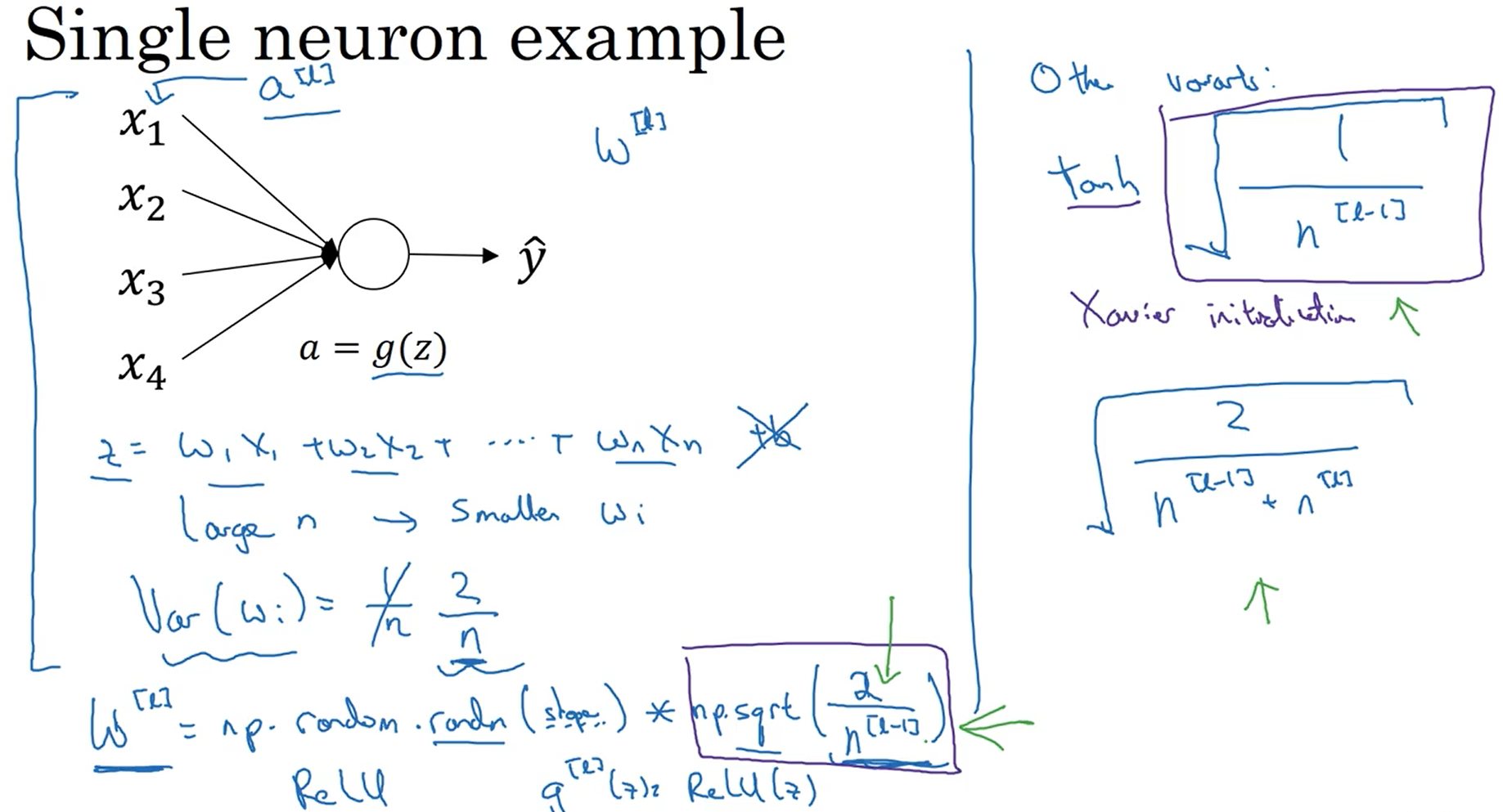
1.11神经网络的权重初始化
对于整个神经网络的研究,我们先从单个神经元节点入手。如下图,为了避免发生梯度爆炸和梯度消失的问题,我们必须要使神经网络在传播的过程中保持方差一致,所以我们令前后的方差都为1,根据方差的公式,参数w的方差为1/n(对于不同的激活函数值不同),所以初始化参数w时有下图中的那一行代码。randn函数会生成一个服从标准正态分布的随机样本值,当乘以1/n的平方根后方差为1/n(这里我也不知道为什么要开平方,之后知道了来补坑)。
参考博文:https://zhuanlan.zhihu.com/p/27919794,这篇文章解释了xvaier初始化。
1.12梯度的数值逼近
之所以要进行梯度的数值逼近是因为计算机并不能像人类一样对函数进行准确的求导,它只能通过数值对导数进行近似的计算,在进行计算的过程中,使用双边误差的效果更好,如下图。

1.13梯度检验
对于每层的变量进行梯度的数值逼近,然后比较数值逼近的梯度值与实际的梯度值是否接近,标准是两者之间的欧几里得范数值除以两个向量的长度值之和,也就使进行归一化操作,若结果小于10-7则程序中不存在bug,否则程序中可能存在bug。

1.14关于梯度检验实现的注记
在使用梯度检验时要注意下图的几点。

二.优化算法
2.1Mini-batch梯度下降法
当我们使用大量数据训练模型时,如下图使用500万条数据,由于使用之前的梯度下降算法每次梯度下降都要对500万条数据进行处理,虽然使用向量化,但由于数据太多,处理起来会比较慢。所以我们令mini-batch为1000,也就是每1000个数据为一组,这样500万条数据分为5000组。

下图是mini-batch梯度下降算法的执行步骤:对于每一次梯度下降,对于每一个组都要进行梯度下降,也就是之前的一次梯度下降是对500万条数据整体进行一次梯度下降,而现在的一次梯度下降分别对每组进行一次梯度下降,也就是进行5000次梯度下降。首先有一个对每个组的循环遍历,然后对每个组的梯度下降过程与之前的梯度下降过程是一样的,根据需要也可以对成本函数进行正则化。

2.2理解mini-batch梯度下降法
下图给出了batch梯度下降法和mini-batch梯度下降法在迭代过程中成本函数值的变化,从图中可以看出,对于batch梯度下降算法的成本函数值一般是单调递减的;对于mini-batch梯度下降法来说,由于第一组数据可能使成本函数值下降,而第二组数据的成本函数比第一组数据的要高,这就使得噪声比较大。
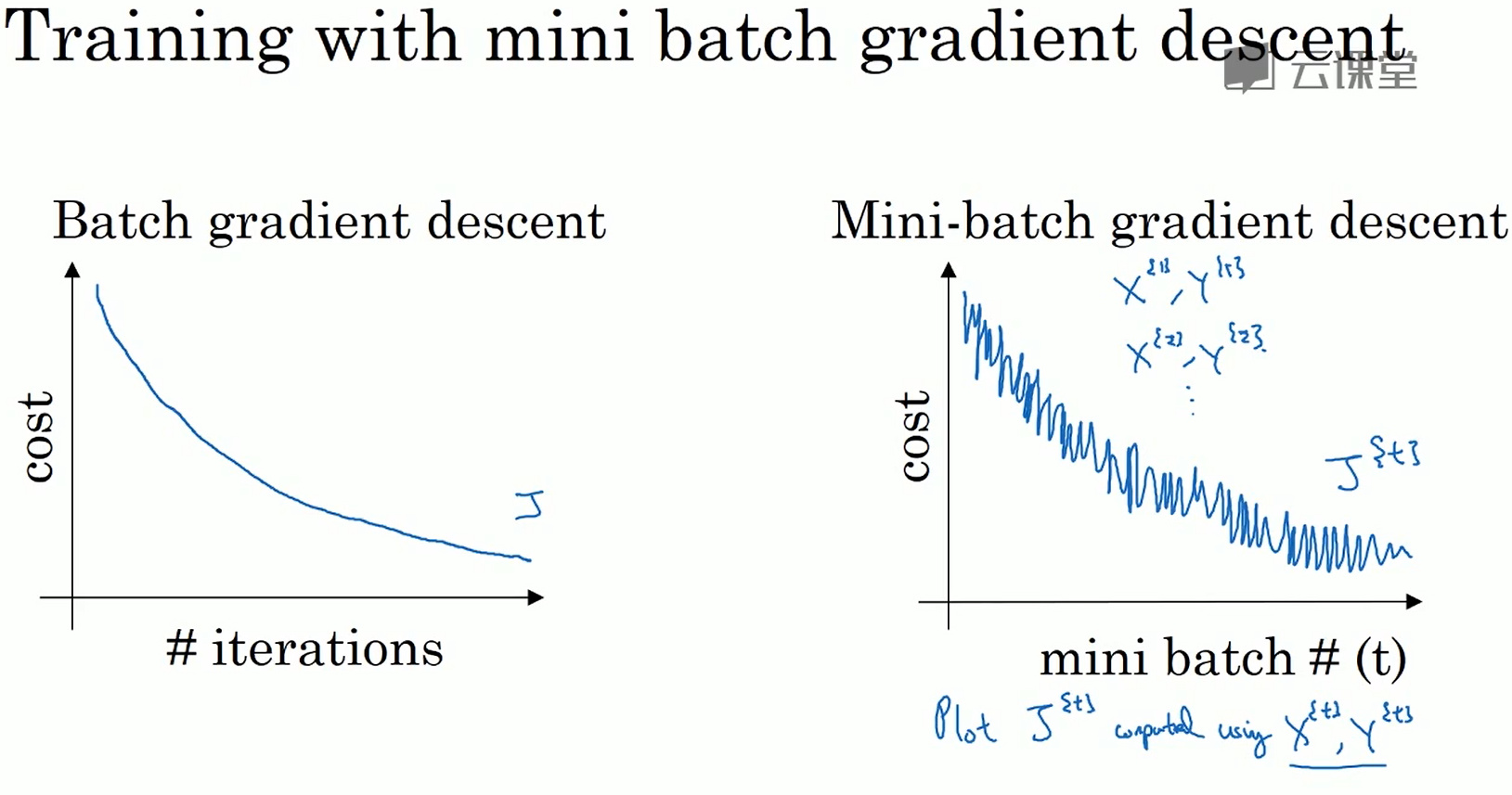
那mini-batch的值要如何选择呢?当它的值为m时,整个样本都被分到同一个组中了,此时与batch梯度下降算法完全相同。当它的值为1时,batch梯度下降算法变为随机梯度下降算法,这时每一个样本为一组,无法发挥向量化的作用。所以mini-batch的大小要介于1与m之间,这样既能发挥向量化的作用,又可以不用等整个训练集处理完再进行下面的工作。当样本总数小于2000时,使用batch梯度下降算法,反之使用mini-batch,而且mini-batch的大小最好为2的指数的形式。

最后解释一下为什么mini-batch的效率更高:对于batch梯度下降算法而言,每次遍历完所有样本后才会进行梯度下降并更新参数值,而mini-batch只要遍历完一组后就会进行梯度下降更新参数值,所以效率更高。
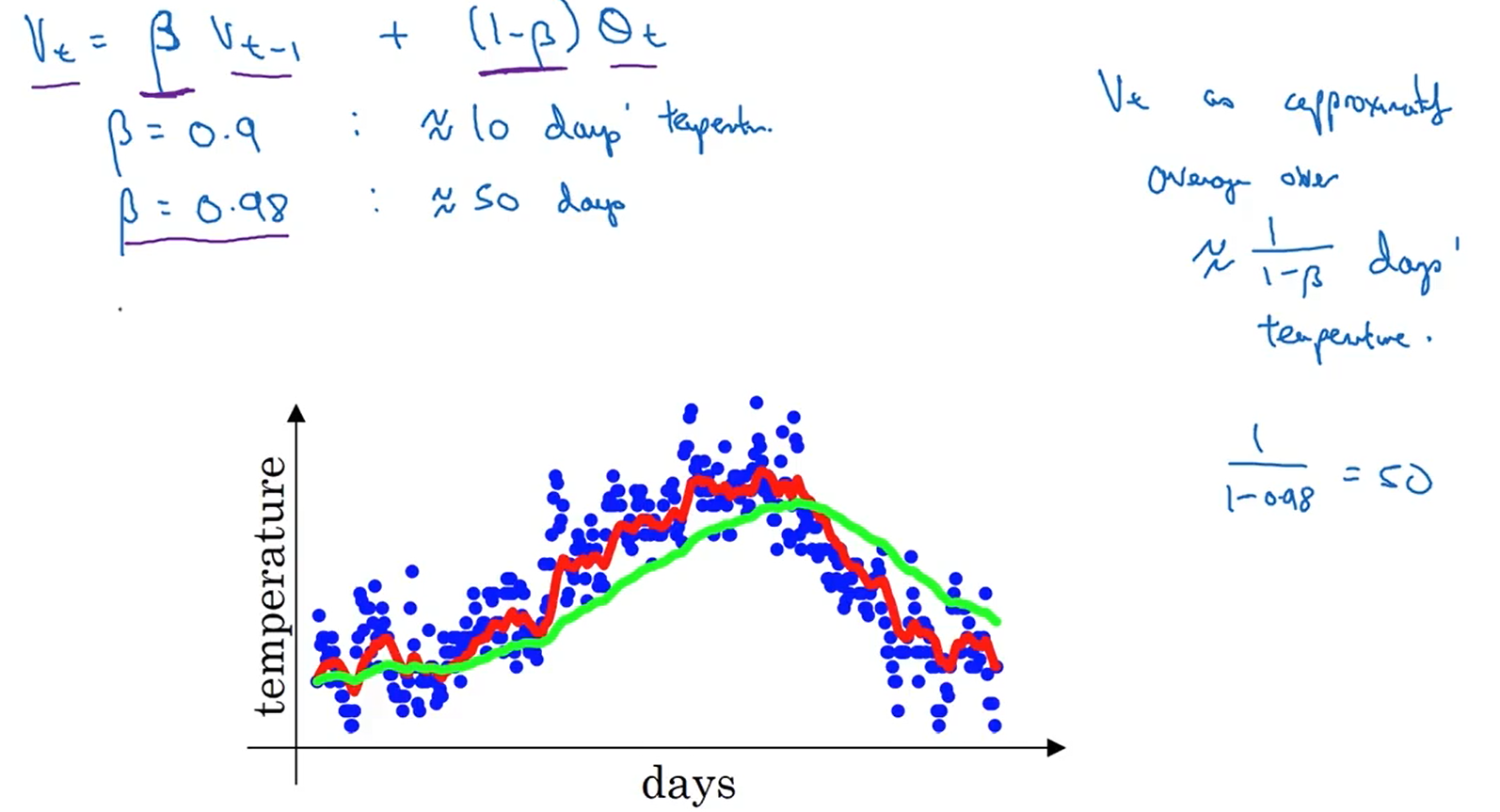
2.3指数加权平均
根据下图中的公式,若β的值为0.9,则大约为10天温度的平均值。
2.4理解指数加权平均
通过下图我们直观的理解一下指数加权平均算法:这里我们取β的值为0.9,我们从第v100向v1方向进行推导,将v100的关系是展开,我们可以发现每天的气温数据的系数是按照指数比例递减的,这里我们以1/e为分界点,当衰减到这个值后忽略不计,那多久才能衰减到呢?答案是1/(1-β)。所以当β取0.9时,可以看作是10天温度的平均。

那指数加权平均与算数平均相比的优势在哪里呀?指数加权是一种近似求平均的方法,其效果比不上加权平均。但是从下图可以看出,指数加权平均的每一步运算是在上一步运算的基础上进行的,所以它只需要在内存中占用一行的存储空间,而算数平均需要将所有的数据都保存下来后才能求平均值,不利于对大量数据进行运算。

2.5指数加权平均的偏差修正
当使用指数加权平均算法对数据均值进行预测的初期并不准确,所以我们使用下图中的公式对结果进行修正。可以看出当t很大时,βt趋近于0,此时与未修正时的结果接近,所以主要对初期的均值进行修正。
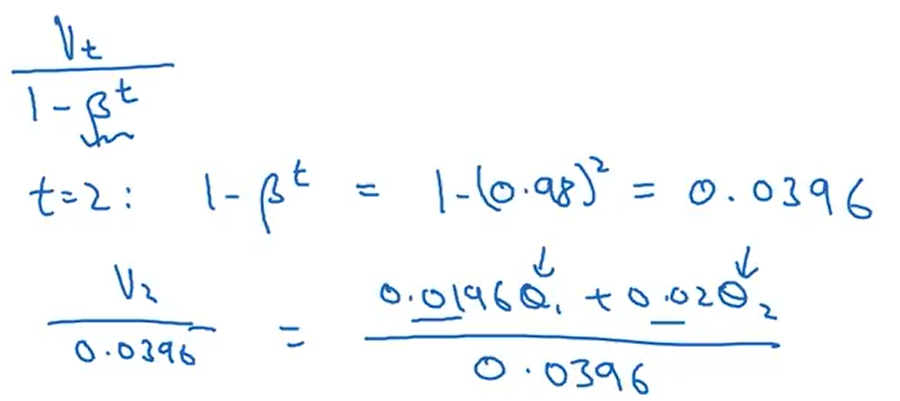
2.6动量梯度下降法
在学习momentum算法前我们要了解一下mini-batch梯度下降算法的缺陷,mini-batch梯度下降算法将训练集进行划分,加快了模型的迭代速度,但是由于每次梯度下降都是针对随机抽取的一部分样本,所以每次下降并不是严格按照朝最小方向下降,会出现震荡的情况,但是总体下降趋势是朝着最小方向,从下图可以看出:
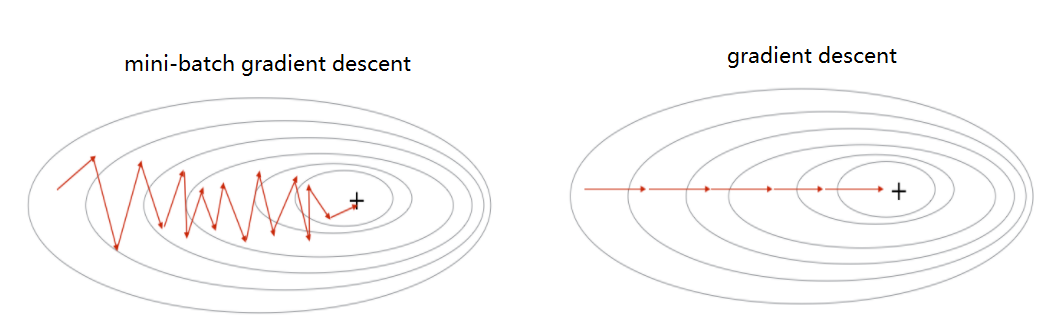
由于有震荡的情况,所以针对mini-batch梯度下降法不能使用较大的学习率,因为可能导致更新后的函数值超过函数的界限,而momentum算法就是为了解决mini-batch的缺陷。
momentum算法要计算vdw,该值是近期dw的指数加权平均值,超参数β一般取0.9,此时表示最近十个dw的平均值。这个过程一般不需要偏差修正。

动量梯度下降法主要针对mini-batch梯度下降算法进行优化,优化之后左右摆动更小,从而提高效率。
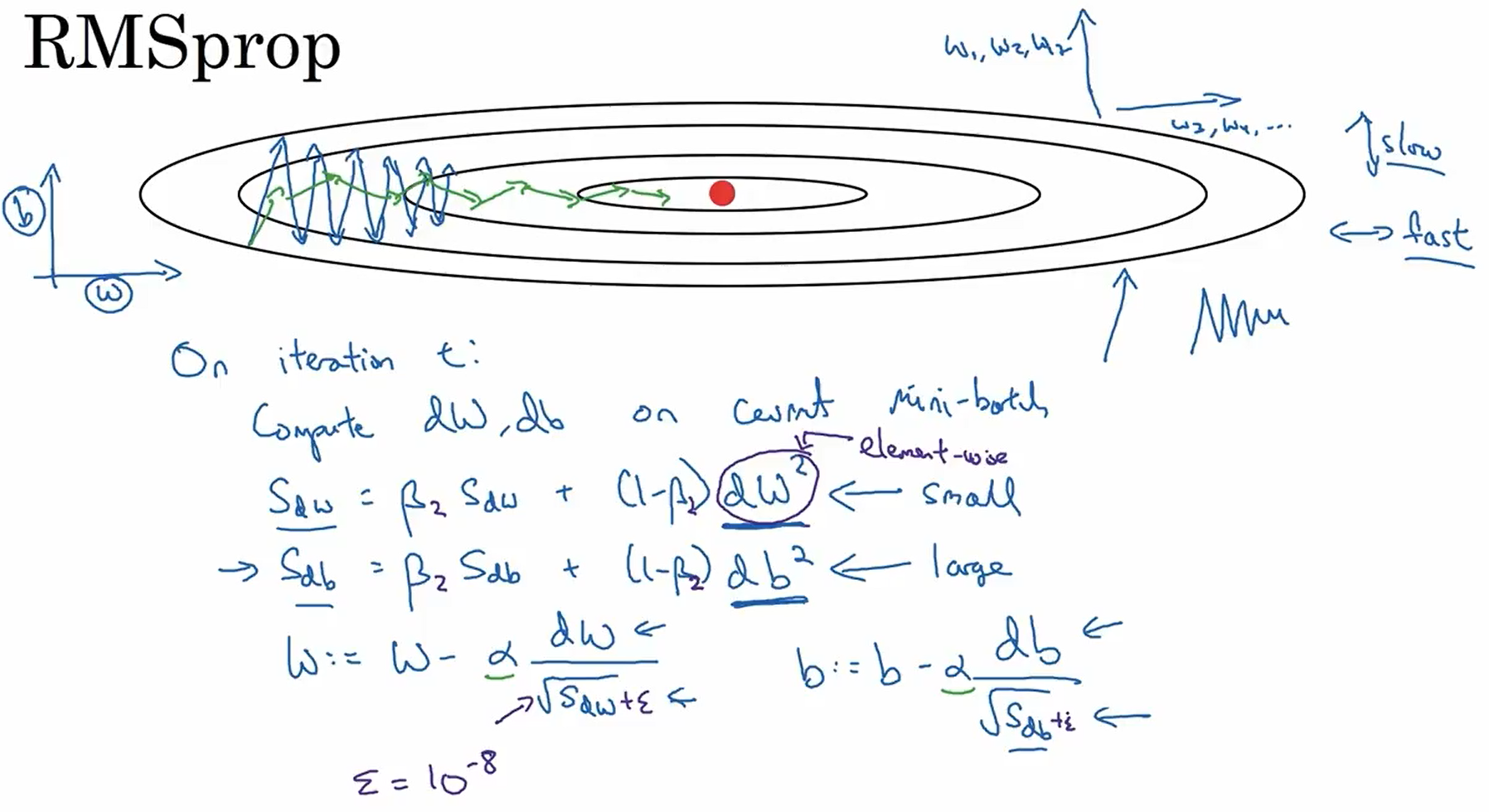
2.7RMSprop
RMSprop主要用于对mini-batch梯度下降算法进行优化,减少迭代过程中的摆动并允许使用更大的学习率来加快迭代过程,下图是RMSprop的具体公式:
2.8Adam优化算法
Adam优化算法的具体公式如下:

超参数的推荐值如下:

2.9学习率衰减
从下图我们可以看出,当我们使用mini-batch梯度下降算法时,由于迭代过程中有噪音,所以虽然是朝最小值下降,但是不会精确收敛。但是如果慢慢减少学习率的话,在初期时学习率是比较大的,学习还是较快的,但是随着学习率逐渐减小,迭代的步伐也会渐渐变小,最后结果会在最小值附近的一小块区域里摆动,这就是使用学习率衰减的原因。
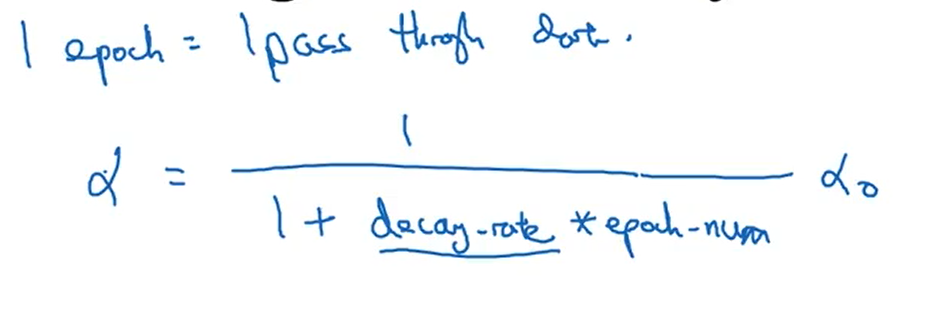
我们称对所有的样本的一次迭代为一代。下图为几种学习率衰减的公式:

2.10局部最优问题
在大型神经网络中(有很多参数,高维空间),局部最优问题通常很难遇到,更多的问题在于鞍点。

三.超参数调试、Batch正则化和程序框架
3.1调试处理
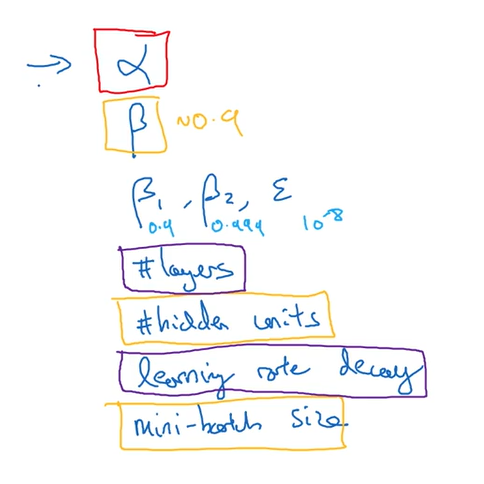
下图中是一些需要调试的超参数,红框中是最重要的,黄框中是次重要的,紫框中是相对最不重要的。
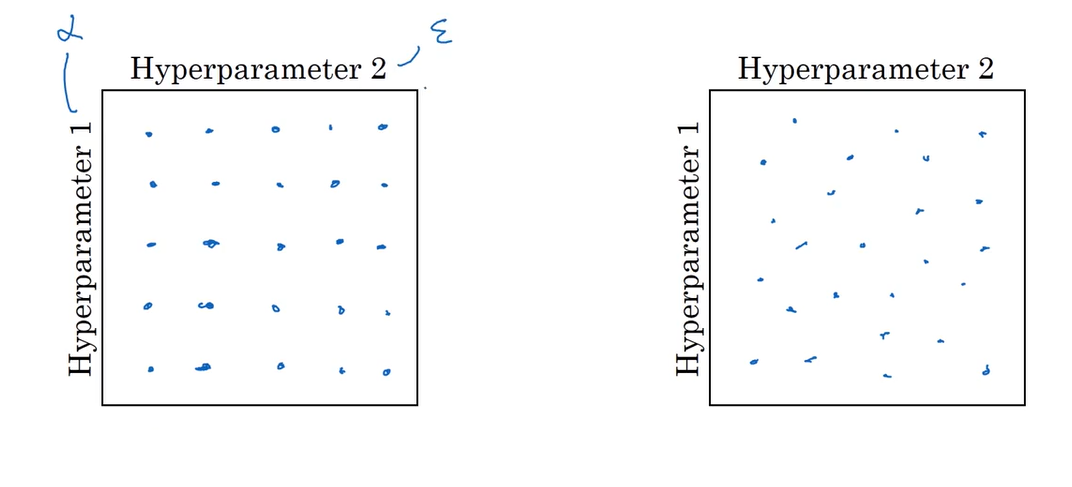
如果要调试的一个二参数,最好使用随机调试的方式而不是网格调试。因为如果是网格调试,每个参数只能测试五个值,而随机调试最多可以测25个值。如果参数更多,测试的维数也会变多。
在随机取样的过程中,如果发现某个区域内的效果比较好,可以把区域放大后再随机取样。

3.2为超参数选择合适的范围
对于一些超参数,比如神经网络的层数和每层神经网络的节点数来说我们可以使用线性轴均匀取值来进行调试。
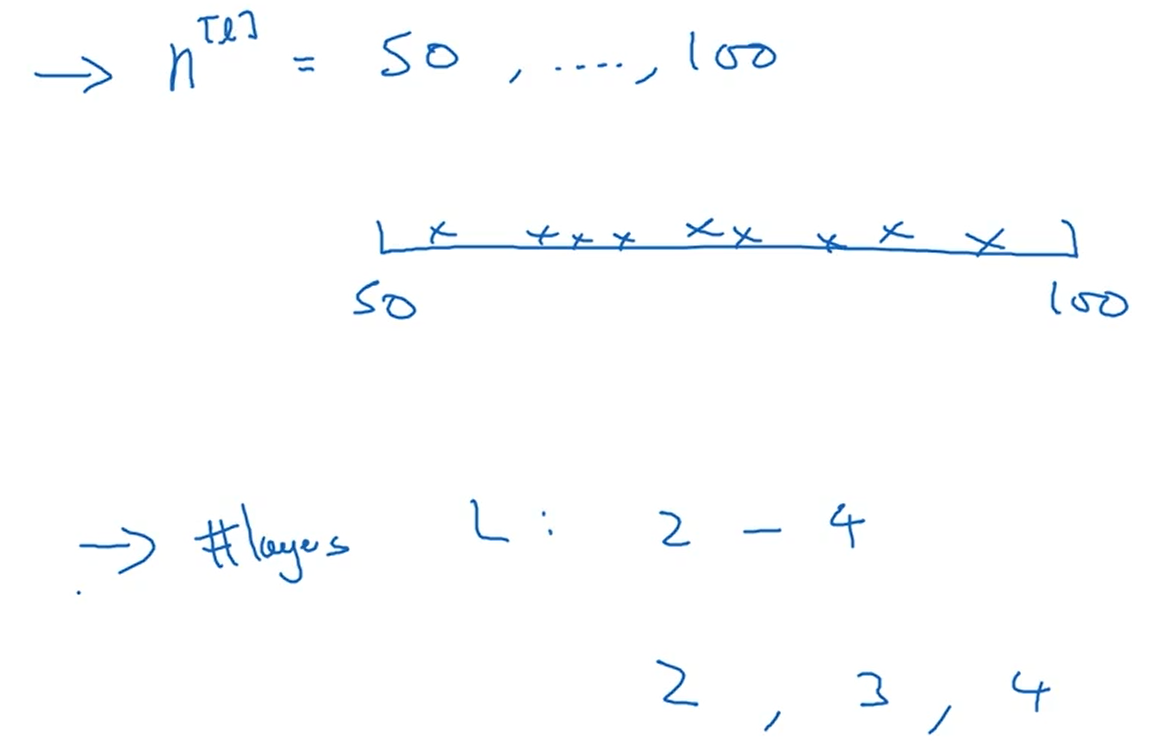
但是对于一些来说线性轴并不适用,比如学习率。因为对于一些参数来说,如下图,其在[0.0001,0.1]上对神经网络的影响要比在[0.1,1]上大很多,但是如果使用线性轴进行调试,在[0.0001,0.1]上取值的比率只有0.1,而在[0.1,1]上取值的比率有0.9。在这种情况下要使用对数轴进行均匀取值,具体取值方法见下图。

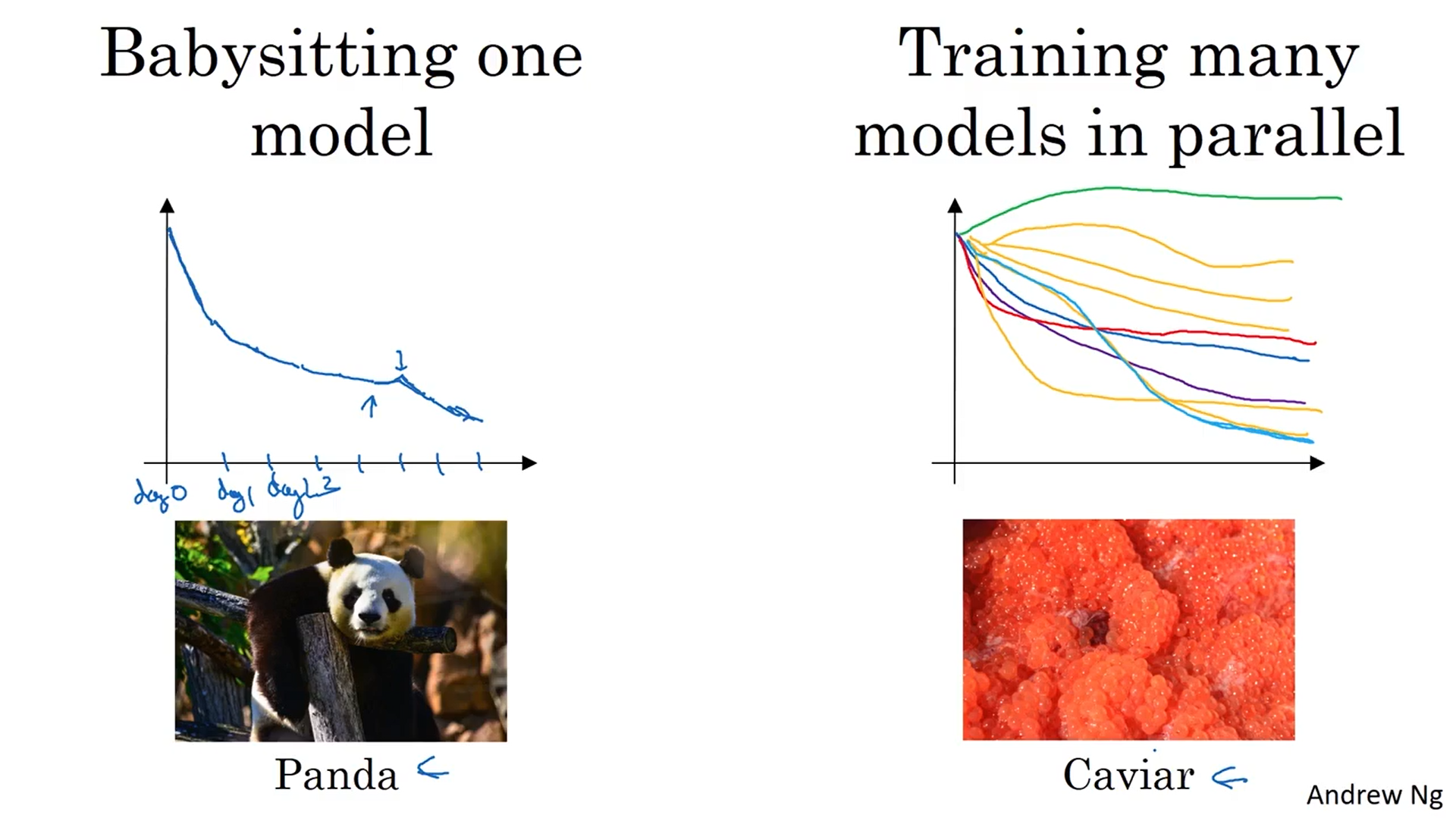
3.3Pandas VS Cavair
下图是训练神经网络的两种方式,左边适用于训练资源比较少的情况,此时对一个模型进行训练,在训练过程中逐渐对参数进行调试并观察成本函数的变化情况;右边适用于训练资源比较多的情况,可以同时对多个模型进行训练,每个模型都有不同的参数取值,从中选出最好的使用。
3.4正则化网络的激活函数
使用下图的方式可以对每一层的z进行归一化,这样可以加快迭代速度。
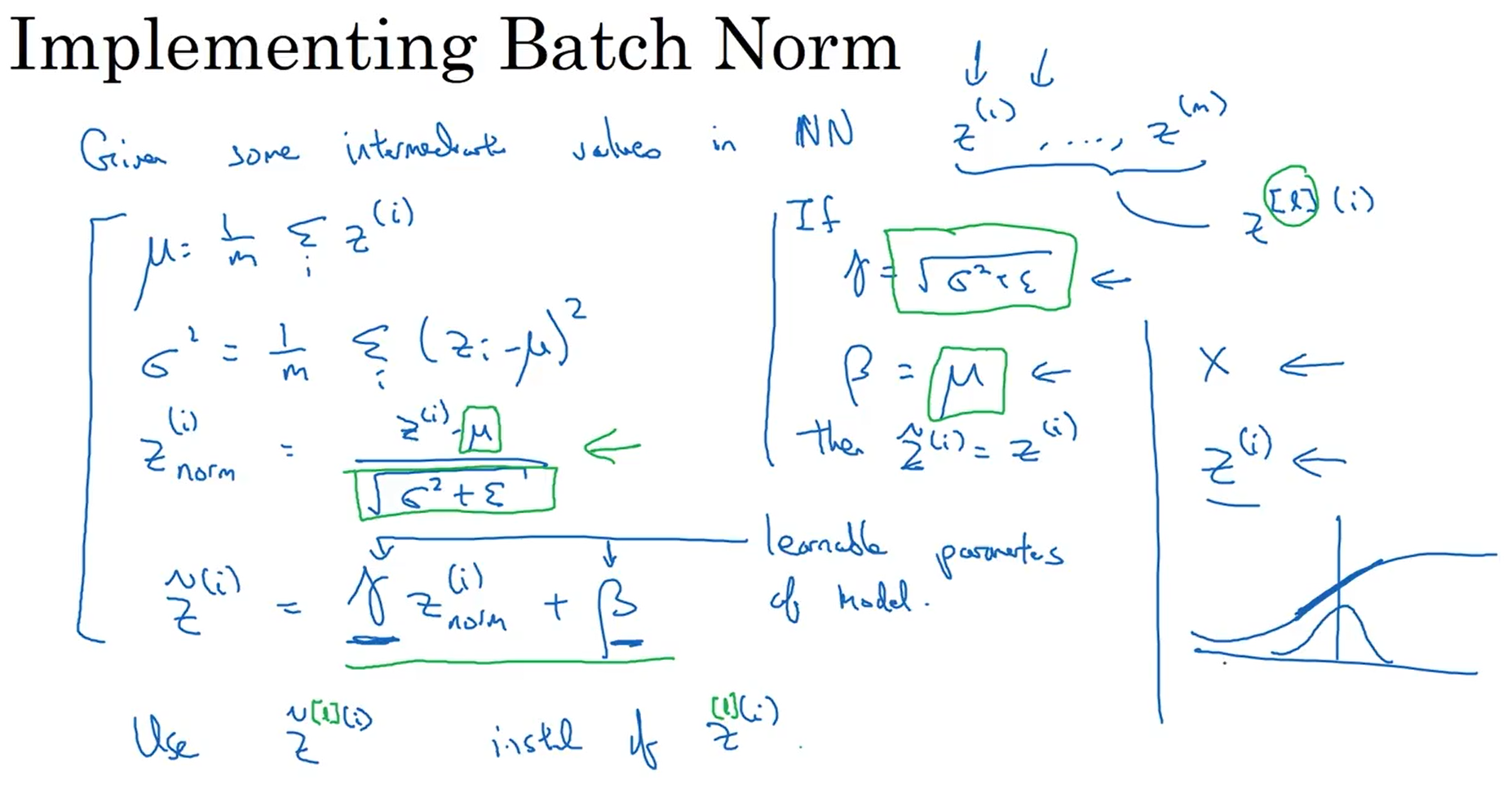
3.5将Batch Norm拟合进神经网络
下图是将batch-norm结合到mini-batch梯度下降算法的过程,当使用batch-norm时,参数b无效。

3.6Batch Norm为什么奏效?
在学习的过程中,对于一个中间的隐藏层来说,其输入值会变的不一样,但是Batch Norm会对该层的输入数据进行归一化,使其均值和方差保持不变,这样在很大程度上减少了数据的变化,降低了前面隐藏层的参数对后面参数的影响,有利于更好地学习。其次,Batch Norm还有轻微正则化的作用,它会向隐藏层加入少量的噪音,有轻微正则化的作用。
3.7测试时的Batch Norm
在训练时,我们计算的均值和方差是基于一个mini-batch的样本,而测试的过程中,均值和方差是基于所有的样本,使用的是指数加权平均。
3.8Softmax回归
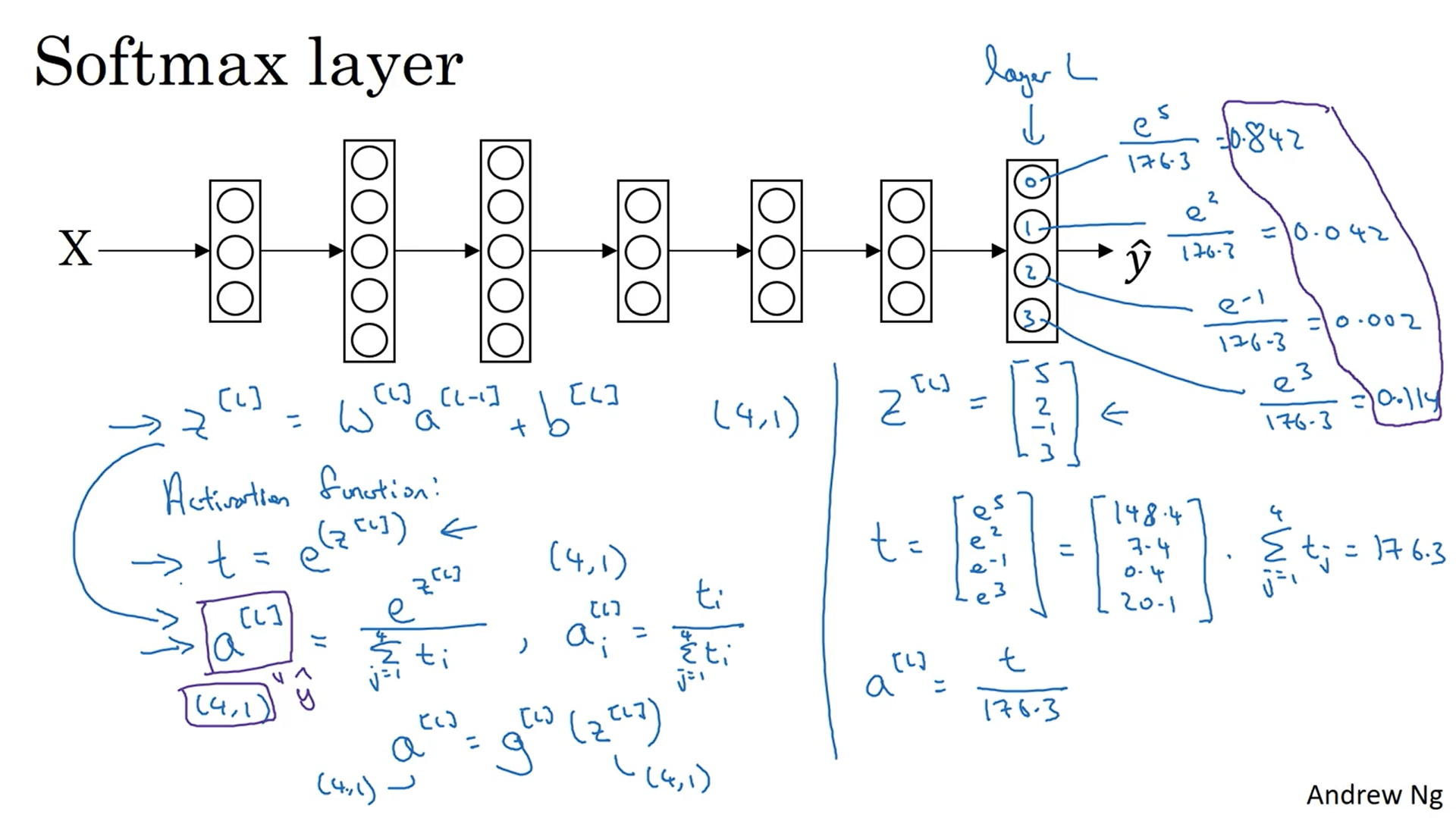
Softmax激活函数将多个标量映射为一个概率分布,其输出的每一个值范围在(0,1),经常用在神经网络的最后一层,作为输出层,进行多分类。具体计算过程如下:
3.9训练一个Softmax分类器
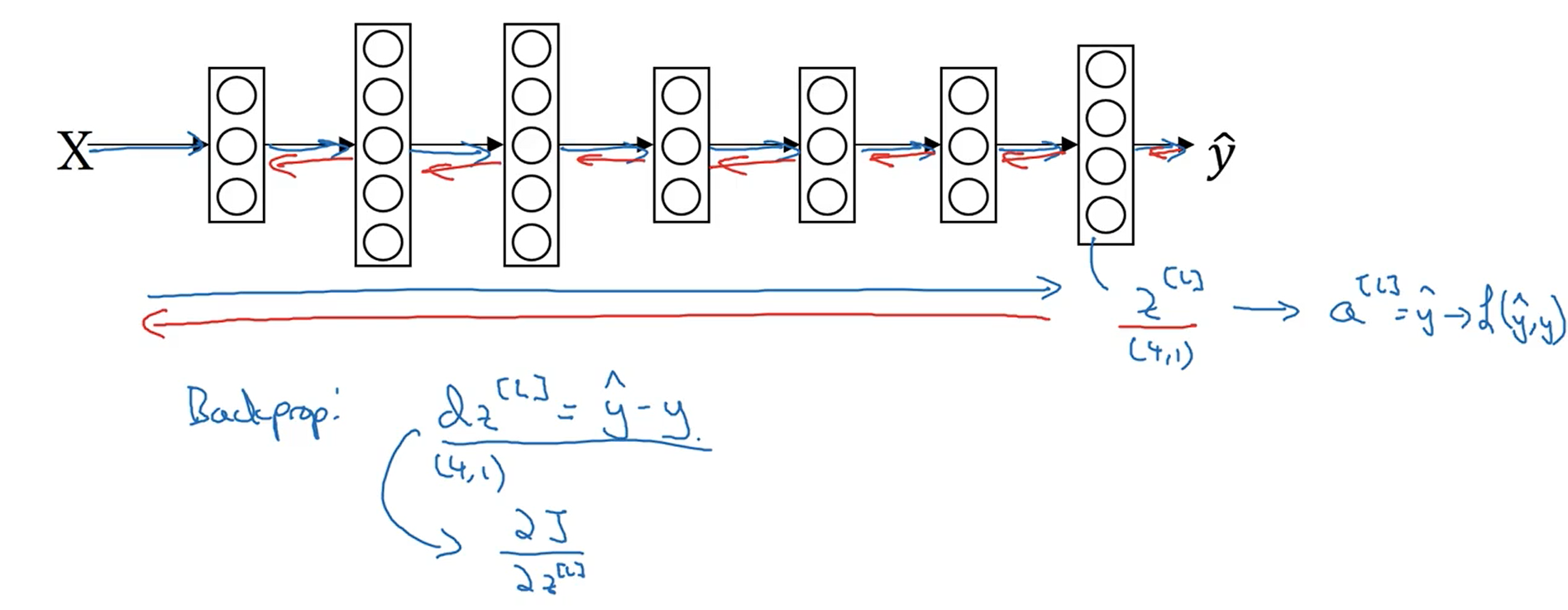
下图展示了Softmax层进行正向传播和反向传播的过程。
3.10深度学习框架
下图是一些常用的框架和选择的标准。



