Dijkstra算法（Swift版）

原理

我们知道，使用Breadth-first search算法能够找到到达某个目标的最短路径，但这个算法没考虑weight,因此我们再为每个edge添加了权重后，我们就需要使用Dijkstra算法来寻找权重和最小的路径。

其实原理很简单，我们最终的目的是计算出每一个节点到起点的权重之和，同时获取得到这个权重和的路径数组。
那么权重和最小的那个自然就是我们要的结果。

在该算法中有一下几个核心的思想：

• 当我们遍历到某个节点时，计算出该节点到起点的权重和之后=，该节点就不在使用了，或删除或者标记为已检阅
• 当该节点的某个neighbor节点加上权重的值小于该neighbor节点时，跟新该neighbor节点的数据

实现这个算法的方式有多种，在该文章中，我们把某些数据直接封装到了节点中。

Vertex

Vertex.swift

import Foundation

open class Vertex {

    open var identifier: String
    open var neighbors: [(Vertex, Double)] = []
    open var pathLengthFromStart = Double.infinity
    open var pathVerticesFromStart: [Vertex] = []

    public init(identifier: String) {
        self.identifier = identifier
    }

    open func clearCache() {
        pathLengthFromStart = Double.infinity
        pathVerticesFromStart = []
    }
}

extension Vertex: Hashable {
    open var hashValue: Int {
        return identifier.hashValue
    }
}

extension Vertex: Equatable {
    public static func ==(lhs: Vertex, rhs: Vertex) -> Bool {
        return lhs.hashValue == rhs.hashValue
    }
}

Dijkstra

Dijkstra.swift

import Foundation

public class Dijkstra {
    private var totalVertices: Set<Vertex>

    public init(vertices: Set<Vertex>) {
        totalVertices = vertices
    }

    private func clearCache() {
        totalVertices.forEach { $0.clearCache() }
    }

    public func findShortestPaths(from startVertex: Vertex) {
        clearCache()
        var currentVertices = self.totalVertices
        startVertex.pathLengthFromStart = 0
        startVertex.pathVerticesFromStart.append(startVertex)
        var currentVertex: Vertex? = startVertex
        while let vertex = currentVertex {
            currentVertices.remove(vertex)
            let filteredNeighbors = vertex.neighbors.filter { currentVertices.contains($0.0) }
            for neighbor in filteredNeighbors {
                let neighborVertex = neighbor.0
                let weight = neighbor.1

                let theoreticNewWeight = vertex.pathLengthFromStart + weight
                if theoreticNewWeight < neighborVertex.pathLengthFromStart {
                    neighborVertex.pathLengthFromStart = theoreticNewWeight
                    neighborVertex.pathVerticesFromStart = vertex.pathVerticesFromStart
                    neighborVertex.pathVerticesFromStart.append(neighborVertex)
                }
            }
            if currentVertices.isEmpty {
                currentVertex = nil
                break
            }
            currentVertex = currentVertices.min { $0.pathLengthFromStart < $1.pathLengthFromStart }
        }
    }
}

演示

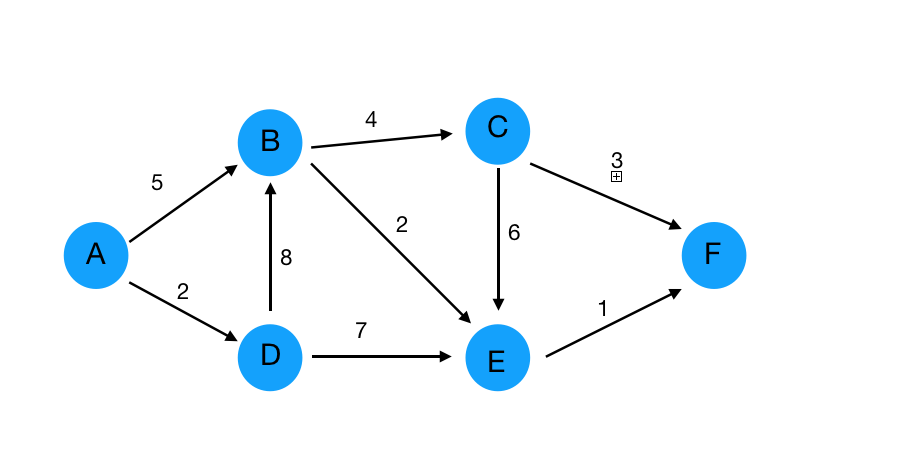
我们就演示这个例子

//: Playground - noun: a place where people can play
import Foundation

// last checked with Xcode 9.0b4
#if swift(>=4.0)
print("Hello, Swift 4!")
#endif

var vertices: Set<Vertex> = Set()

/// Create vertexs
var vertexA = Vertex(identifier: "A")
var vertexB = Vertex(identifier: "B")
var vertexC = Vertex(identifier: "C")
var vertexD = Vertex(identifier: "D")
var vertexE = Vertex(identifier: "E")
var vertexF = Vertex(identifier: "F")

/// Setting neighbors
vertexA.neighbors.append(contentsOf: [(vertexB, 5), (vertexD, 2)])
vertexB.neighbors.append(contentsOf: [(vertexC, 4), (vertexE, 2)])
vertexC.neighbors.append(contentsOf: [(vertexE, 6), (vertexF, 3)])
vertexD.neighbors.append(contentsOf: [(vertexB, 8), (vertexE, 7)])
vertexE.neighbors.append(contentsOf: [(vertexF, 1)])

vertices.insert(vertexA)
vertices.insert(vertexB)
vertices.insert(vertexC)
vertices.insert(vertexD)
vertices.insert(vertexE)
vertices.insert(vertexF)


let dijkstra = Dijkstra(vertices: vertices)
dijkstra.findShortestPaths(from: vertexA)

for vertex in vertices {
    let paths = vertex.pathVerticesFromStart.map({ $0.identifier })
    print("(A=>" + vertex.identifier + "): " + paths.joined(separator: " -> "))
}

打印结果：

(A=>B): A -> B
(A=>A): A
(A=>F): A -> B -> E -> F
(A=>C): A -> B -> C
(A=>D): A -> D
(A=>E): A -> B -> E

主要代码来自于Dijkstra