对局匹配

问题描述

　　小明喜欢在一个围棋网站上找别人在线对弈。这个网站上所有注册用户都有一个积分，代表他的围棋水平。


　　小明发现网站的自动对局系统在匹配对手时，只会将积分差恰好是K的两名用户匹配在一起。如果两人分差小于或大于K，系统都不会将他们匹配。


　　现在小明知道这个网站总共有N名用户，以及他们的积分分别是A1, A2, ... AN。


　　小明想了解最多可能有多少名用户同时在线寻找对手，但是系统却一场对局都匹配不起来(任意两名用户积分差不等于K)？
输入格式
　　第一行包含两个个整数N和K。
　　第二行包含N个整数A1, A2, ... AN。


　　对于30%的数据，1 <= N <= 10
　　对于100%的数据，1 <= N <= 100000, 0 <= Ai <= 100000, 0 <= K <= 100000
输出格式
　　一个整数，代表答案。
样例输入
10 0
1 4 2 8 5 7 1 4 2 8
样例输出
6

Algorithm

一般来讲求最值问题可以考虑动态规划，这个题目亦是如此。
我们假设分值分布为下图所示：

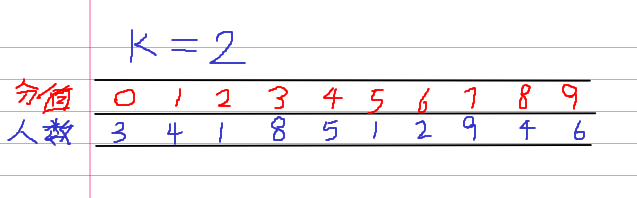
那么我们可以得到两个以公差为K的等差数列

0 2 4 6 8

1 3 5 7 9

那么我们可以想到，相邻的两个数我们不能选，因为他们相差K，我们的任务就是选取这几个分数所对应的人数，使它们的人数最大（有点背包问题的味道）

先考虑只有一个分数：

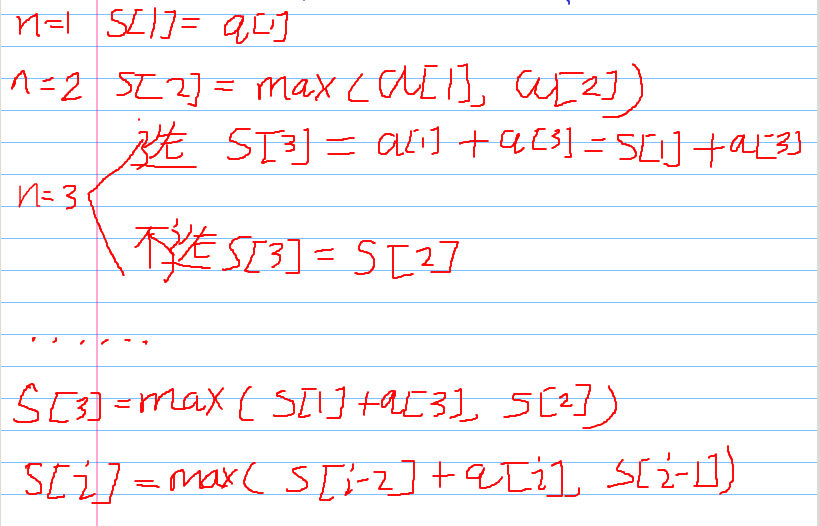
有了状态转移方程，我们就得到了一个分组的最大值。还有一个数列是1 3 5 7 9.

对于K=0特殊处理一下即可，不重复的数字个数即为答案，可以用二叉搜索树去重。

 

AC 

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<set>
 5 
 6 using namespace std;
 7 
 8 const int MAX = 1e5 + 7;
 9 
10 int N, K, x;
11 int B[MAX];
12 int cnt = 0;
13 set<int> s;        // 二叉搜索树去重 
14 
15 inline int max(int a, int b) {return a>b?a:b;}
16 
17 // 动态规划 
18 int dp(int *a, int n)
19 {
20     if(n == 0) return 0;
21     if(n == 1) return a[0];
22     if(n == 2) return max(a[1], a[0]);
23      int s[MAX];
24     memset(s, 0, sizeof(s));
25     s[0] = a[0]; s[1] = max(a[1], a[0]);
26      for(int i=2;i<n;i++){
27         s[i] = max(s[i-1], s[i-2]+a[i]);
28     }
29     return s[n-1];
30 }
31 
32 int main()
33 {
34     while(cin>>N>>K)
35     {
36         memset(B, 0, sizeof(B));
37         bool book[MAX];
38         memset(book, true, sizeof(book));
39         for(int i=0;i<N;i++){
40             scanf("%d", &x);
41             s.insert(x);
42             B[x]++;
43         }
44         if(!K){
45             cout<<s.size()<<'\n';
46             continue;
47         }
48         if(N == 1){
49             cout<<1<<'\n';
50             continue;
51         }
52         int ans = 0;
53         for(int i=0;i<N;i++){
54             // 从第 i 个数开始构造公差为 K 的等差数列 
55             int t = 0;
56             if(book[i]){        //这个数没有用过 
57                 int temp[MAX];
58                 memset(temp, 0, sizeof(temp));
59                 temp[t++] = B[i];
60                 book[i] = false;
61                 for(int j=i+1;j<MAX;j++){
62                     if((j - i)%K == 0){
63                         temp[t++] = B[j];
64                         book[j] = false;
65                     }
66                 }
67                 if(t) ans += dp(temp, t);
68             }
69         }
70         cout<<ans<<'\n';
71     }
72 
73     return 0;
74 }
View Code

2019-03-08

20:34:05

posted @ 2019-03-08 20:34  maybeTang  阅读(229)  评论(0)  编辑  收藏  举报