矩阵翻硬币

问题描述

　　小明先把硬币摆成了一个 n 行 m 列的矩阵。

　　随后，小明对每一个硬币分别进行一次 Q 操作。

　　对第x行第y列的硬币进行 Q 操作的定义：将所有第 i*x 行，第 j*y 列的硬币进行翻转。

　　其中i和j为任意使操作可行的正整数，行号和列号都是从1开始。

　　当小明对所有硬币都进行了一次 Q 操作后，他发现了一个奇迹——所有硬币均为正面朝上。

　　小明想知道最开始有多少枚硬币是反面朝上的。于是，他向他的好朋友小M寻求帮助。

　　聪明的小M告诉小明，只需要对所有硬币再进行一次Q操作，即可恢复到最开始的状态。然而小明很懒，不愿意照做。于是小明希望你给出他更好的方法。帮他计算出答案。
输入格式
　　输入数据包含一行，两个正整数 n m，含义见题目描述。
输出格式
　　输出一个正整数，表示最开始有多少枚硬币是反面朝上的。
样例输入
2 3
样例输出
1
数据规模和约定
　　对于10%的数据，n、m <= 10^3；
　　对于20%的数据，n、m <= 10^7；
　　对于40%的数据，n、m <= 10^15；
　　对于10%的数据，n、m <= 10^1000（10的1000次方）。

Algorithm

很容易想到如果一个硬币被翻转了奇数次，那么它的状态就会发生改变，在这里，我们翻转奇数次的硬币就是我们之前反面朝上的硬币。

如果一个硬币的坐标为(x, y)，那么它被翻转的次数为a x b 次，若想要这个硬币被翻奇数次，a和b必须都得是奇数，即x和y都有奇数个约数。

这个题的思路我是从这里get的，最开始我也想过要模拟，但是发现数据不允许，那么想来就一定是什么高深的数学知识或者巧妙的数据结构了。
但是，最后发现这就是一个高精度问题 ~_~
不过还是有点数学学问在里边，不管我之前知不知道，反正我现在是记住了：完全平方数有奇数个约数

AC

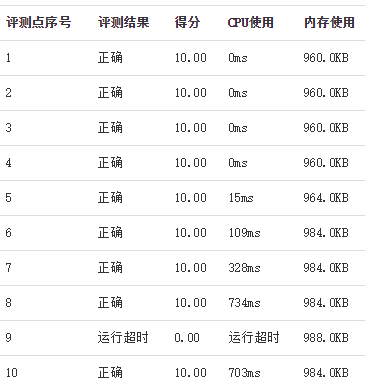
不知道为什么第9组数据没有通过，可能我还需要优化吧......

  1 #include<iostream>
  2 #include<string>
  3 #include<cstring>
  4 
  5 using namespace std;
  6 
  7 typedef long long ll;
  8 // MAX 有上限  85000
  9 const ll MAX = 1009;
 10 
 11 // 大数乘法 
 12 string BigMul(string x, string y)
 13 {    // 据说可以分治优化
 14     string ret;
 15     ll lenx = x.length();
 16     ll leny = y.length();
 17     // 被乘数、乘数、积 
 18     ll a[MAX], b[MAX], c[MAX];
 19     memset(a, 0, sizeof(a));
 20     memset(b, 0, sizeof(b));
 21     memset(c, 0, sizeof(c));
 22     for(ll i=lenx-1;i>=0;i--)
 23         a[lenx-i] = x[i] - '0';
 24     for(ll i=leny-1;i>=0;i--)
 25         b[leny-i] = y[i] - '0';
 26     // 第 i 位乘以 第 j 位为积的第 i+j-1 位(先不考虑进位) 
 27     for(ll i=1;i<=lenx;i++)
 28         for(ll j=1;j<=leny;j++)
 29             c[i+j-1] += a[i]*b[j];
 30     // 处理进位 
 31     for(ll i=1;i<=lenx+leny;i++)
 32         c[i+1] += c[i]/10, c[i] %= 10;
 33     // 判断第 i+j 位是否为 0  
 34     if(c[lenx+leny]) ret += c[lenx+leny] + '0';
 35     for(ll i=lenx+leny-1;i>=1;i--)
 36         ret += c[i] + '0';
 37     
 38     return ret;
 39 }
 40 
 41 // 大数比较大小 
 42 bool BigNumCmp(string a, string b)
 43 {
 44     if(a == b) return true;
 45     ll la = a.length();
 46     ll lb = b.length();
 47     if(la > lb) return true;
 48     if(la < lb) return false;
 49     for(ll i=0;i<la;i++){
 50         if(a.at(i) == b.at(i)) continue;
 51         if(a.at(i) < b.at(i)) return false;
 52         if(a.at(i) > b.at(i)) return true;
 53     }
 54 }
 55 
 56 // 大数开方 
 57 string BigSqrt(string x)
 58 {
 59     string ret;
 60     ll len = x.length();
 61     ll ls = 0, i = 0;
 62     if(len&1) ls = (len>>1) + 1;
 63     else ls = len>>1;
 64     for(ll i=0;i<ls;i++) ret += "0";
 65     if(BigMul(ret, ret) == x) return ret;
 66     while(ls--)
 67     {    
 68         for(int k=0;k<10;k++){
 69             if(BigMul(ret, ret) == x) return ret;
 70             if(!BigNumCmp(BigMul(ret, ret), x)){
 71                 ret.at(i)++;
 72                 if(ret.at(i) == ':'){
 73                     ret.at(i)--;break;
 74                 }
 75             }
 76             else{
 77                 ret.at(i)--;break;
 78             }
 79         }
 80         i++;
 81     }
 82     
 83     return ret;
 84 }
 85 
 86 int main()
 87 {
 88     string a, b;
 89     char A[2*MAX];
 90     // while(scanf("%s%s", &a[0], &b[0]))
 91     gets(A);
 92     {    
 93         int i=0;
 94         for(;i<strlen(A);i++){
 95             if(A[i] == ' '){
 96                 i++;break;
 97             }
 98             a.push_back(A[i]);
 99         }
100         for(;i<strlen(A);i++) b.push_back(A[i]);
101         // cout<<BigMul(a, b)<<'\n';
102         // cout<<BigNumCmp(a, b)<<'\n';
103         // cout<<BigSqrt(a)<<'\n';
104         // cout<<BigMul(BigSqrt(a), BigSqrt(b))<<'\n';
105         // puts(BigMul(BigSqrt(a), BigSqrt(b)).c_str());
106         cout<<BigMul(BigSqrt(a), BigSqrt(b))<<'\n';
107     }
108     
109     return 0;
110 }
View Code

2019-02-25

21:20:50

posted @ 2019-02-25 21:23  maybeTang  阅读(540)  评论(0)  编辑  收藏  举报