数字预失真（DPD）小试

前言

射频功放的增益响应并非线性的，受到放大管饱和效应的影响，功放不可避免地出现非线性、甚至具有记忆效应的失真。这种非线性失真不仅产生高阶谐波，还会产生互调干扰，降低带内信噪比，影响带外信号。因此，需要一种方式减弱射频功放的非线性增益，数字预失真就是方式之一。ADI有篇文章不错，看完之后基本可以独立实现DPD算法。

RF通信的数字预失真：从等式到实现方案

本文将从 信号产生->失真模拟->失真模型检验->逆模型检验效果 四个部分验证DPD算法在双音与多音通信系统中的matlab验证。

信号产生

采样率1MHz 生成90kHz、100kHz、110kHz三音信号，采样点数16384。

%% 信号产生
fs = 1e6;
f1 = 90e3;
f2 = 100e3;
f3 = 110e3;
N = 1024 * 16;
N_FFT = N;
tmax = N / fs;
t = linspace(0, tmax, N);
sig_in = sin(2 * pi * f1 .* t) + sin(2 * pi * f2 .* t) + sin(2 * pi * f3 .* t);
sig_in = sig_in / max(sig_in);

失真模型

射频功放PA部分，使用saleh模型模拟无记忆失真，使用FIR滤波器模拟记忆效应。

%% 建立带记忆功放失真模型
b = [0.7692 0.1538 0.0769]; %《射频功放数字预失真线性化技术研究_詹鹏》
a = [1];
% 使用saleh模型模拟无记忆失真，使用FIR滤波器模拟记忆效应，检测该模型的AM/AM与AM/PM
u = linspace(0, 1, N);
PA_out_u = saleh(filter(b, a, u));

figure(1)
subplot(2, 1, 1)
plot(u, abs(PA_out_u));
hold on
plot(u, u);
hold off;
title("AM/AM")
xlabel("sig in")
ylabel("PA out")
subplot(2, 1, 2)
plot(u, angle(PA_out_u));
title("AM/PM")
xlabel("sig in")
ylabel("PA out")


PA_out = saleh(filter(b, a, sig_in););
figure(2)
clf
plot(real(PA_out))
hold on
plot(real(sig_in))
hold off
plt_fft(PA_out', fs, 3, 1);
ylim([-80 0])
xlim([0 200e3])
ylabel("功率谱")
xlabel("f/Hz")
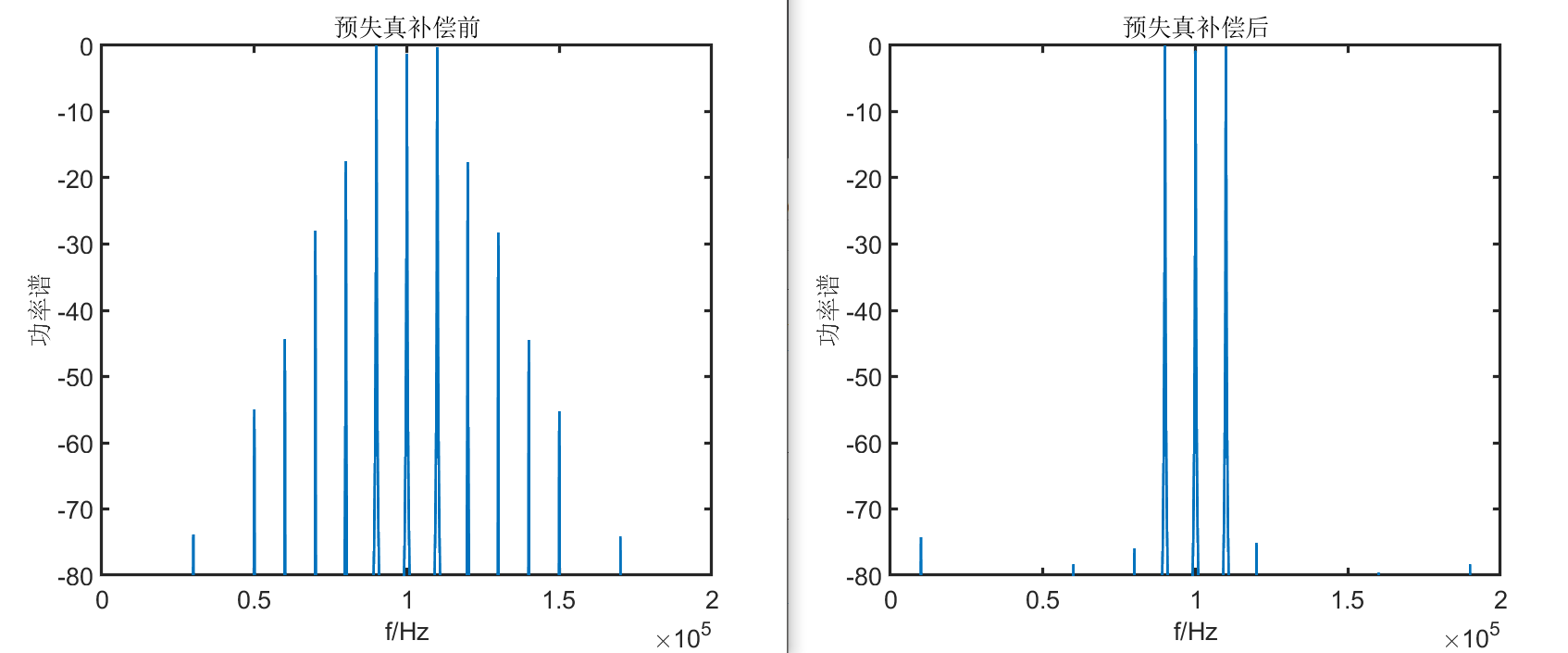
title("预失真补偿前")

• 其中saleh模型如下：

  点击查看代码

  function y = saleh(x)
  	%para = [2.1587 1.1517 4.0033 9.1040];
  	para = [1.5 0.5 pi/3 1];
  	a1 = para(1); b1 = para(2);
  	a2 = para(3); b2 = para(4);
  	ain = abs(x);
  	thetain = angle(x);
  	aout = a1 .* ain ./ (1 + b1 .* ain .^ 2);
  	thetapm = a2 * ain .^ 2 ./ (1 + b2 .* ain .^ 2);
  	thetaout = thetain + thetapm;
  	y = aout .* exp(1j * thetaout);
  end
  
  

• plt_fft是画图部分，代码如下

  点击查看代码

  function []=plt_fft(x, fs, num,t1)
  	L = length(x);
  	Y = fft(real(x.*hann(L)));
  	P2 = abs(Y / L);
  	P1 = P2(1:L / 2 + 1);
  	P1(2:end - 1) = 2 * P1(2:end - 1);
  	f = fs * (0:(L / 2)) / L;
  	if t1==1
  		P1=20*log10(abs(P1/max(P1)));
  	else
  		P1=20*log10(abs(P1));
  	end
  	figure(num)
  	plot(f, P1)
  end
  

失真模型检验

预失真部分，使用简化的广义记忆多项式模型，不包含交叉项，这样虽然丢失了一部分记忆效应，但是计算量骤减。

%% 建立预失真
x = sig_in;
y = PA_out;
x = x.';
y = y.';
K = 7;
M = 3;

X = MP_model(x, K, M);
Y = MP_model(y, K, M);

% 拟合测试，判断阶数与记忆深度是否匹配
U = MP_model(u.', K, M);
X_H = X';
w_test = pinv(X_H * X) * X_H * y;
y_dis = U * w_test;
figure(6)
subplot(2, 1, 1)
plot(u, u);
hold on
plot(u, abs(PA_out_u));
hold on
plot(u, abs(y_dis));
hold off;
legend(["line" "PA_out_u" "GMP_u"])
title("AM/AM")
xlabel("sig in")
ylabel("PA out")
subplot(2, 1, 2)
plot(u, angle(y_dis));
title("AM/PM")
xlabel("sig in")
ylabel("PA out")
hold off;

• 其中MP_model是构建GMP部分，代码如下

  点击查看代码

  function [Y] = MP_model(x_i, K, M)
  
  for m=0:M
  	x=mat_delay(x_i, m);
  	for k=0:K
  		if k==0
  			H=x;
  		else
  			H=[H,x.*(abs(x).^k)];
  		end
  	end
  	if m==0
  		Y=H;
  	else
  		Y=[Y,H];
  	end
  end
  
  

• 其中mat_delay是记忆部分，代码如下

  点击查看代码

  function x_d = mat_delay(x, dd)
  
  	if dd == 0
  		x_d = x;
  	else
  		x_d = circshift(x, dd);
  		x_d(1:dd, 1) = 0;
  	end
  
  end
  
  

逆模型检验效果

%% 使用逆模型构建预失真
Y_H = Y';
w = pinv(Y_H * Y) * Y_H * x;
X_pre = X * w;
PA_out2 = saleh(filter(b,a,X_pre));

figure(4)
plot(real(PA_out2))
hold on
plot(real(PA_out))
hold off
plt_fft(PA_out2, fs, 5, 1);
ylim([-80 0])
xlim([0 200e3])
ylabel("功率谱")
xlabel("f/Hz")
title("预失真补偿后")

效果

github

• 主文件为main_detail.m，详见注释
  github地址