FM的一种简易解调方式

理论来源

• 《高低频电路设计与制作》 铃木雅臣 著。这位作者的书写的都不错

电路图

• 模拟思路
  
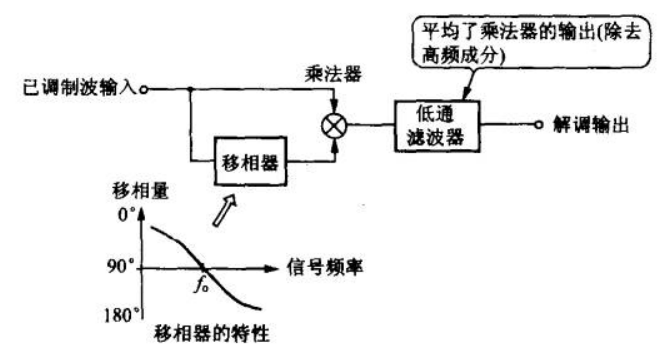
  设输入信号为

  \[s(t) = \sin(w_0 t + \Delta w\int_{- \infty }^{t} m(\tau ) d\tau ) \]

  注意看书中，所谓的“移相”，本质上是一个延时器，相位在中心频率处移相90°，中心频率两测近似线性变化。利用一些滤波器可实现该电路。
  设延时\(\Delta t = \frac{\pi}{2 w_0}\)，延时后信号：

  \[s_{2}(t) = \sin(w_0 t + \int_{- \infty }^{t+\Delta t } m(\tau ) d\tau +\frac{\pi}{2} ) \]

  相乘再低通滤波，有

  \[s_{3}(t) = \cos(\int_{- \infty }^{t+\Delta t } m(\tau ) d\tau - \int_{- \infty }^{t} m(\tau ) d\tau +\frac{\pi}{2} ) \]

  化简

  \[s_{3}(t) = \sin(\int_{t}^{t+\Delta t } m(\tau ) d\tau ) \]

  由于基频远超过信号频率，因此\(\Delta t\)极小，有

  \[s_{3}(t) \approx \int_{t}^{t+\Delta t } m(\tau ) d\tau \approx \Delta t m(t) \]

  缺点是信号需要后级放大
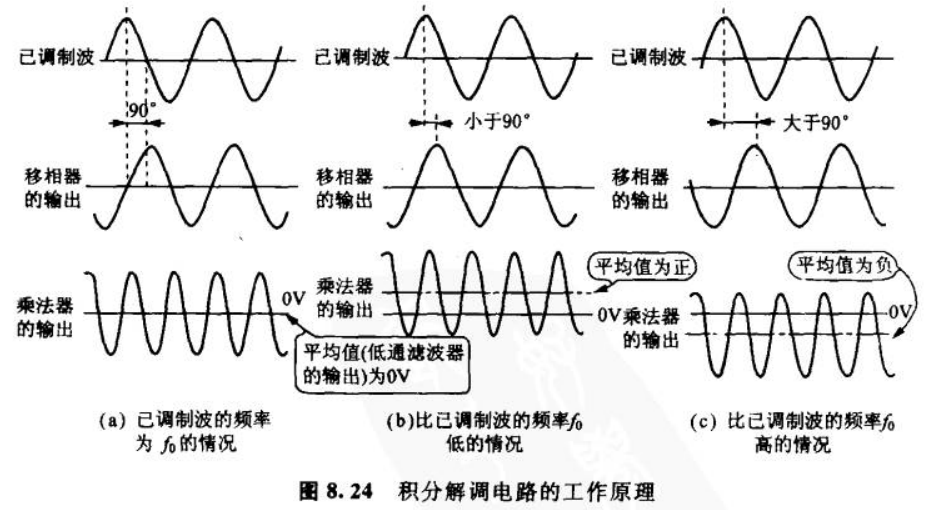
  实际上延时\(\Delta t\)也不一定非要为90°，只是在90°和270°附近更好一些

  从另一种角度来看，这就是利用乘法器实现鉴相解调过程，由于延时操作，频率变化对应了相位的变化，乘法器将相位变化表现为偏置的变化，滤波后产生输出波形
  

• 利用数字电路实现鉴相
  
  
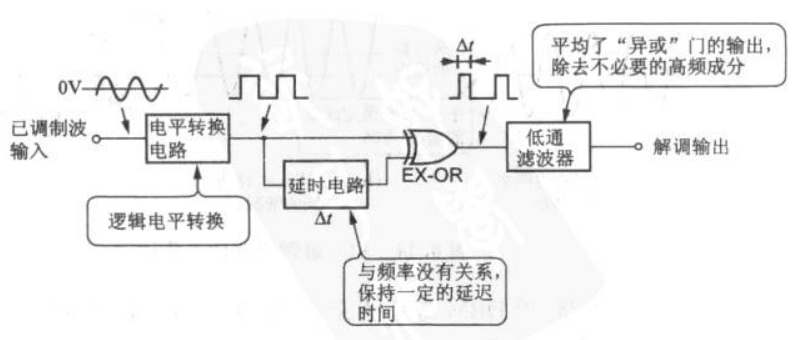
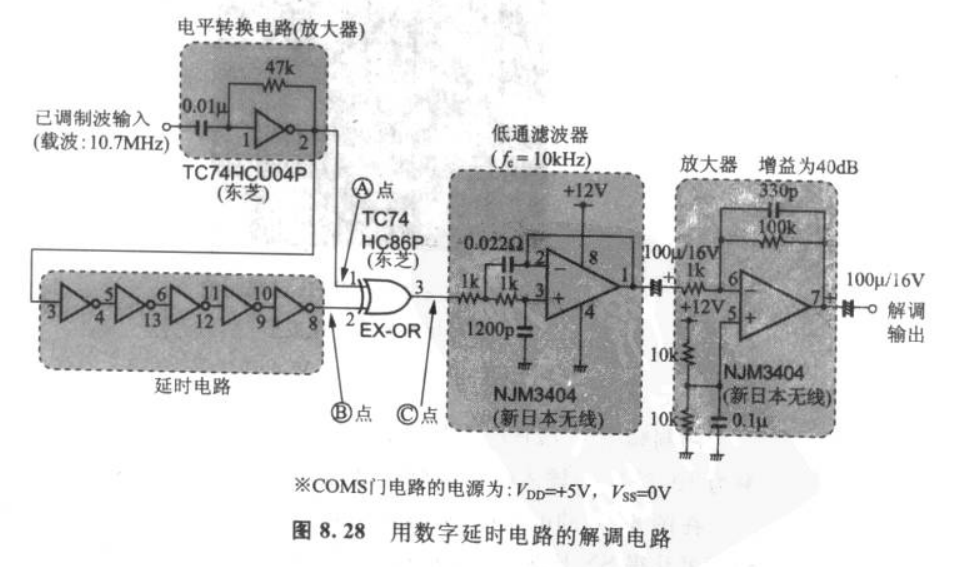
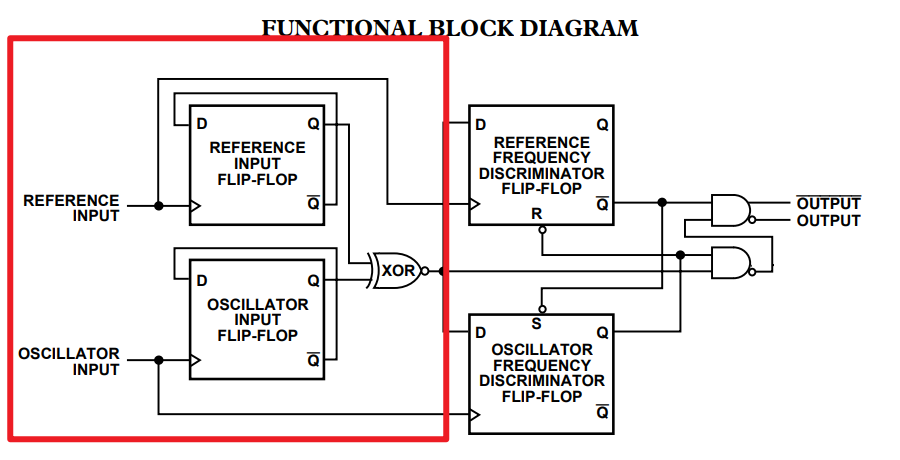
  实际上是把FM 先进行了1bit量化，仅保留频率信息；利用延迟电路设置延迟，通过异或门将延迟信号相对源信号的相移量以1bit量化形式输出（是个鉴相器），最后由滤波器实现\(\Sigma\)积分器的作用，全程等效于用$ \Delta \Sigma $开环鉴相器方式实现解调，对比看一看集成鉴相器：
  
  参考信号为原信号，跟踪信号为延迟信号，由于延迟导致相位-频差近似线性关系，因此通过XOR鉴相得到的相位差就是调制信号

  据书上说明，信噪比可达到80dB以上，妈妈再也不用担心调锁相环调到头秃啦