希尔伯特变换用于解调系统——以解调调频信号为例,FM Demodulation
What's The Hilbert Transform
简单地说,希尔伯特变换的物理意义为:把信号的所有频率分量的相位推迟90度,这样原信号和变换后信号可以视为一组IQ正交信号,在数字域正交化,可以做很多事情。
有一篇文章写的不错:《希尔伯特变换的物理意义》,这篇文章简单地说明了变换后、变换前之间信号的物理意义,并且可以推出原信号的顺时幅度、顺时相位、顺时频率信息,值得一看。这里仅列出一些后文需要用到的公式。
还有一篇讲解调PM的,也可以看看:Phase demodulation via Hilbert transform: Hands-on
记:
原信号\(s(t)=A(t)\sin (\varphi(t))\)
其中\(A(t)\)为瞬时幅值,\(\varphi(t)\)为瞬时相位
吉尔伯特变换后,有\(\hat{s}(t)=\mathcal{H} \left | s(t) \right |\)
则有\(A(t)=\sqrt{\hat{s}^{2}(t) + s^{2}(t)}\),\(\varphi(t)=\arctan \frac{\hat{s}(t)}{s(t)}\),需要四象限反正切
Demodulation via Hilbert Transform
希尔伯特变换用于单边带调制的案例很多,但是既然希尔伯特变换能单独求出幅值、相位信息,甚至可以认为希尔伯特变换前后结果就是一组IQ信号,那么就可以试着将其用于解调系统。
注意:希尔伯特变换不是因果的,即对于实时解调来说不应该使用希尔伯特变换,如果先采很长时间,之后解调,则希尔伯特变换对于t<0(和t>t_sample)的非因果效应不是很影响主要信号,下文会展示该影响
以调频信号为例,其瞬时相位为
其中\(\omega _s\)为调制信号角频率
设载波100k,调制信号10k,fm频偏5k
对于已调信号,有:
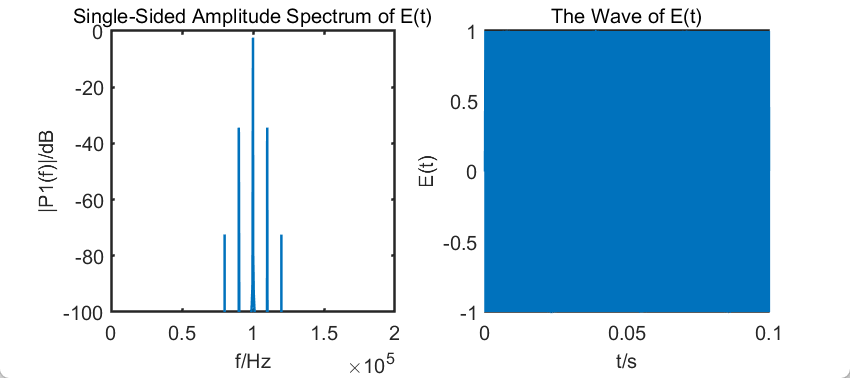
姑且不管右侧时域波形,左侧FM调制频谱更清楚一些。
对信号进行希尔伯特变换后,求出瞬时相位\(\varphi(t)=\arctan \frac{\hat{s}(t)}{s(t)}\),差分后得到基带调制信号:
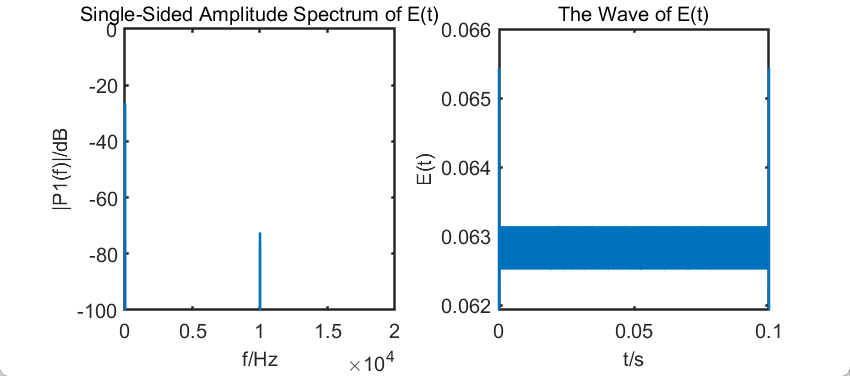
可以看到解调信号时域两端出现干扰,并且具有较大直流分量,这是非因果带来的问题。可以对原信号两端补零减少影响,大家可以动手试一试,这里不再赘述。
Matlab Program
clear;
clc;
tic;
f0 = 100e3; %载波
f1 = 10e3; %调制信号
L = 1e6; %采样长度
tmax = 1e-1; %采样时间
t = linspace(0, tmax, L);
fs = L / tmax;
df = 5e3; %频移量
mf = df / f0; %调频度
%%%%S
phi_t = 2 * pi * f0 .* t + mf * sin(2 * pi * f1 .* t);
s = sin(phi_t); %调频信号
figure(1)
subplot(1, 2, 2);
plot(t, s);
xlabel("t/s")
ylabel("S(t)")
title("The Wave of S(t)")
w = hamming(L); %加窗
Y = fft(1.414 * s .* w'); %我拿Hann的补偿系数乘上去了,大家可以查查Hamming的系数是多少
P2 = abs(Y / L);
P1 = P2(1:L / 2 + 1);
P1(2:end - 1) = 2 * P1(2:end - 1);
f = fs * (0:(L / 2)) / L;
P1 = db(P1);
subplot(1, 2, 1);
plot(f, P1)
title("Single-Sided Amplitude Spectrum of S(t)")
xlabel("f/Hz")
ylabel("|P1(f)|/dB")
xlim([f0 -100e3 f0 +100e3]);
ylim([-100 0]);
%%%%希尔伯特变换
y_t = hilbert(s); %这里其实可以加一个Hann窗或补0,减少信号两端出现混叠
phi = unwrap(angle(y_t)); %matlab的hilbert实部为原信号,虚部为变换信号
s_demod = diff(phi);
L = L - 1; %差分函数会使长度-1
t2 = linspace(0, tmax, L);
figure(2)
clf;
subplot(1, 2, 2);
plot(t2, s_demod);
xlabel("t/s")
ylabel("E(t)")
title("The Wave of S_d(t)")
w = hamming(L);
Y = fft(1.414 * s_demod .* w');
P2 = abs(Y / L);
P1 = P2(1:L / 2 + 1);
P1(2:end - 1) = 2 * P1(2:end - 1);
f = fs * (0:(L / 2)) / L;
P1 = db(P1);
subplot(1, 2, 1);
plot(f, P1)
title("Single-Sided Amplitude Spectrum of S_d(t)")
xlabel("f/Hz")
ylabel("|P1(f)|/dB")
xlim([f1 -10e3 f1 +10e3]);
ylim([-100 0]);
toc;
fprintf('\n 用时:%f s \n', toc);



 浙公网安备 33010602011771号
浙公网安备 33010602011771号