20172318 2018-2019-1 《程序设计与数据结构》第5周学习总结

教材学习内容总结

排序与查找

searching：查找
- 查找是这样一个过程，即在某个项目组中寻找某一指定目标元素，或者确定该指定
  目标并不存在。
- 高效的查找会使该过程所做的比较操作次数最小化·
- searchpool：查找池要查找的一组元素项。
staticmethod 静态方法:通过类名来调用的一种方法，该类名不能引用实例数据。也称
为类方法。
- 在方法声明中，通过使用static修饰符就可以把它声明为静态的·
generic method：泛型方法
- 与创建泛型类相似，我们也可以创建泛型方法。即，不是创建一个引用泛型参数的类，而是创建一个引用泛型的方法。泛型参数只应用于该方法。要创建一个泛型方法，只需在方法头的返回类型前插入一个泛型声明即可：
linearsearch：线性查找:一种查找方式，从列表项的一端开始，按线性方式进行，直到找到要查找的元素，或达到了列表的末端（表明没有找到要查找的元素）。

public static <T>   
		boolean linearSearch(T[] data, int min, int max, T target)
    {
        int index = min;
        boolean found = false;

        while (!found && index <= max) 
        {
            found = data[index].equals(target);
            index++;
        }

        return found;
    }

二分查找法
- binarysearch：二分查找对己排序列表的查找，其中每次比较操作，都可以去除人约一
  半的剩余可行候选元素。
- 二分查找将利用了查找池是已排序的这一事实·
- 二分查找的每次比较都会删除一半的可行候选项。
- logarithmic algorithm对数算法:复杂度为0(g2n）的算法，如二叉查找。
- logarithmic sort：对数排序、种排序算法，如果要给n个元素进行排序，需要大约nlog2n
  次比较操作。

public static <T extends Comparable<T>>  
		boolean binarySearch(T[] data, int min, int max, T target)
    {  
        boolean found = false;
        int midpoint = (min + max) / 2;  // determine the midpoint

        if (data[midpoint].compareTo(target) == 0)
            found = true;

        else if (data[midpoint].compareTo(target) > 0)
        {
            if (min <= midpoint - 1)
                found = binarySearch(data, min, midpoint - 1, target);
        }
        
        else if (midpoint + 1 <= max)
            found = binarySearch(data, midpoint + 1, max, target);

        return found;
    }

二分查找的复杂度是对数级的，这使得它对于大型查找池非常有效率·
sorting：排序
- 排序是这样一个过程，即基于某一标准，将某一组项目接照某个规定顺序排列“
selectionsort：选择排序:算法通过反复地将某一特定值放到它在列表中的最终已排序位置从而完成
对某一列表值的排序

public static <T extends Comparable<T>> 
		void selectionSort(T[] data)
    {
        int min;
        T temp;
        
        for (int index = 0; index < data.length-1; index++)
        {
            min = index;
            for (int scan = index+1; scan < data.length; scan++)
                if (data[scan].compareTo(data[min])<0)
                    min = scan;
			
            swap(data, min, index);
        }
    }

private static <T extends Comparable<T>> 
		void swap(T[] data, int index1, int index2)
	{
		T temp = data[index1];
		data[index1] = data[index2];
		data[index2] = temp;
	}

insertionsort：插入排序:插入排序算法通过反复地将某一特定值插入到该列表某个已排序的子集中来完成对
列表值的排序·

public static <T extends Comparable<T>> 
		void insertionSort(T[] data)
    {
        for (int index = 1; index < data.length; index++)
        {
            T key = data[index];
            int position = index;
			
            // shift larger values to the right 
            while (position > 0 && data[position-1].compareTo(key) > 0)
            {
                data[position] = data[position-1];
                position--;
            }
			
            data[position] = key;
        }
    }

bubble sort：冒泡排序:冒泡排序算法通过重复地比较相邻元素且在必要时将它们互换，从而完成对某个列
表的排序。

public static <T extends Comparable<T>> 
		void bubbleSort(T[] data)
    {
        int position, scan;
        T temp;
		
        for (position =  data.length - 1; position >= 0; position--)
        {
            for (scan = 0; scan <= position - 1; scan++)
            {
                if (data[scan].compareTo(data[scan+1]) > 0)
                    swap(data, scan, scan + 1);
            }
        }
    }

quicksort:快速排序:快速排序算法通过将列表分区，然后对这两个分区进行递归式排序，从而完成对整
个列表的排序·
- partition：分区快速排序算法使用的未排序元素的一个集合，其中的元素个部小于或大
  于选定的某个元素。
- partitionelement：分区元素快速排序算法用来把未排序元素分隔成两个不同分区的
  元素。

public static <T extends Comparable<T>> 
		void quickSort(T[] data)
	{
		quickSort(data, 0, data.length - 1);
	}
	
private static <T extends Comparable<T>> 
		void quickSort(T[] data, int min, int max)
	{
		if (min < max)
		{
			int indexofpartition = partition(data, min, max);
			
			quickSort(data, min, indexofpartition - 1);
			
			quickSort(data, indexofpartition + 1, max);
		}
	}
	
private static <T extends Comparable<T>> 
		int partition(T[] data, int min, int max)
	{
		T partitionelement;
		int left, right;
		int middle = (min + max) / 2;
		
		partitionelement = data[middle];
		swap(data, middle, min);
		
		left = min;
		right = max;
		
		while (left < right)
		{
			while (left < right && data[left].compareTo(partitionelement) <= 0)
				left++;
			
			while (data[right].compareTo(partitionelement) > 0)
				right--;
			
			if (left < right)
				swap(data, left, right);
		}
		
		swap(data, min, right);
		
		return right;
	}

mergesort:归并排序:算法通过将列表递归式分成两半直至每一子列表都含有一个元素，然后将
这些子列表归并到一个排序顺序中，从而完成对列表的排序·

public static <T extends Comparable<T>>
		void mergeSort(T[] data)
	{
		mergeSort(data, 0, data.length - 1);
	}
	
private static <T extends Comparable<T>>
		void mergeSort(T[] data, int min, int max)
	{
		if (min < max)
		{
			int mid = (min + max) / 2;
			mergeSort(data, min, mid);
			mergeSort(data, mid+1, max);
			merge(data, min, mid, max);
		}
	}
	
	
	@SuppressWarnings("unchecked")
private static <T extends Comparable<T>>
		void merge(T[] data, int first, int mid, int last)
	{
		T[] temp = (T[])(new Comparable[data.length]);
		
		int first1 = first, last1 = mid;  // endpoints of first subarray
		int first2 = mid+1, last2 = last;  // endpoints of second subarray
		int index = first1;  // next index open in temp array
		
		while (first1 <= last1 && first2 <= last2)
		{
			if (data[first1].compareTo(data[first2]) < 0)
			{
				temp[index] = data[first1];
				first1++;
			}
			else
			{
				temp[index] = data[first2];
				first2++;
			}
			index++;
		}
		
		while (first1 <= last1)
		{
			temp[index] = data[first1];
			first1++;
			index++;
		}
		
		while (first2 <= last2)
		{
			temp[index] = data[first2];
			first2++;
			index++;
		}
		
		for (index = first; index <= last; index++)
			data[index] = temp[index];
   }

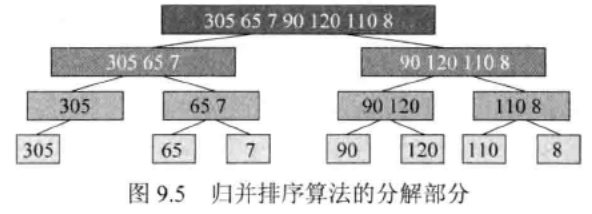
radixsort：基数排序:一种排序算法，使用排序密钥而不是直接地进行比较元素，来实现元素排序
- 基数排序是基于队列处理的。
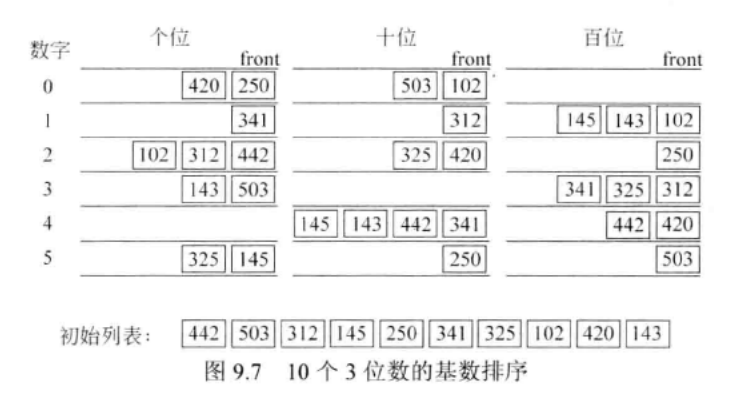
sequentialsort:顺序排序:一种排序算法，通常使用嵌套循环，需要大约n2次比较来给n
个元素排序。
targetelement：目标元素:在查找操作中要寻找的元素。
viablecandidates:可行候选:查找池中的元素，在这些元素中可能找到目标元素。

教材学习中的问题和解决过程

问题1：各个排序法的时间和空间复杂度
问题1解决方案：
问题2：各个排序法的应用场景
问题2解决方案：
(1)若n较小(如n≤50)，可采用直接插入或直接选择排序。
　当记录规模较小时，直接插入排序较好；否则因为直接选择移动的记录数少于直接插人，应选直接选择排序为宜。
(2)若文件初始状态基本有序(指正序)，则应选用直接插人、冒泡或随机的快速排序为宜；
(3)若n较大，则应采用时间复杂度为O(nlgn)的排序方法：快速排序、堆排序或归并排序。
　快速排序是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；
　堆排序所需的辅助空间少于快速排序，并且不会出现快速排序可能出现的最坏情况。这两种排序都是不稳定的。
　若要求排序稳定，则可选用归并排序。但前面介绍的从单个记录起进行两两归并的排序算法并不值得提倡，通常可以将它和直接插入排序结合在一起使用。先利用直接插入排序求得较长的有序子序列，然后再两两归并之。因为直接插入排序是稳定的，所以改进后的归并排序仍是稳定的。

作者：Seven17000
来源：CSDN
原文：https://blog.csdn.net/mbuger/article/details/67643185?utm_source=copy
版权声明：本文为博主原创文章，转载请附上博文链接！

代码调试中的问题和解决过程

问题1：pp9.2运行出现
问题1解决方案：这是一个非常常见的异常，从名字上看是数组下标越界错误，解决方法就是查看为什么下标越界。
for (int j = 0;j<=data.length-i;j++) {
这是我错误的条件，后来我发现应该这样写for (int j = 0;j<=data.length-1-i;j++) {
最后测试成功
问题2：如何获取程序执行时间？
参考了博客java获取程序执行时间
第一种是以毫秒为单位计算的。

//伪代码

long startTime=System.currentTimeMillis(); //获取开始时间

doSomeThing(); //测试的代码段

long endTime=System.currentTimeMillis(); //获取结束时间

System.out.println("程序运行时间： "+(end-start)+"ms");

//伪代码

long startTime=System.currentTimeMillis(); //获取开始时间

doSomeThing(); //测试的代码段

long endTime=System.currentTimeMillis(); //获取结束时间

System.out.println("程序运行时间： "+(end-start)+"ms");
第二种是以纳秒为单位计算的。

//伪代码

long startTime=System.nanoTime(); //获取开始时间

doSomeThing(); //测试的代码段

long endTime=System.nanoTime(); //获取结束时间

System.out.println("程序运行时间： "+(end-start)+"ns");

//伪代码

long startTime=System.nanoTime(); //获取开始时间

doSomeThing(); //测试的代码段

long endTime=System.nanoTime(); //获取结束时间

System.out.println("程序运行时间： "+(end-start)+"ns");

上周考试错题总结

上周无错题

代码托管

点评过的同学博客和代码

本周结对学习情况
- 20172312
- 课本内容总结详细，图片较少
- 结对学习内容
  - 课本第九章

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	0/0	1/1	8/8
第二周	500/500	1/2	15/ 23
第三周	802/1302	1/3	12/35
第四周	1530/2832	2/5	15/50
第五周	1165/3997	1/6	10/60

参考资料

《Java软件结构与数据结构教程（第四版）》

posted @ 2018-10-16 17:33 m1sty 阅读(647) 评论(1) 编辑收藏举报

刷新页面返回顶部

m1sty

20172318 2018-2019-1 《程序设计与数据结构》第5周学习总结

20172318 2018-2019-1 《程序设计与数据结构》第5周学习总结

教材学习内容总结

排序与查找

教材学习中的问题和解决过程

代码调试中的问题和解决过程

上周考试错题总结

代码托管

点评过的同学博客和代码

学习进度条

参考资料

公告