Armstrong公理系统



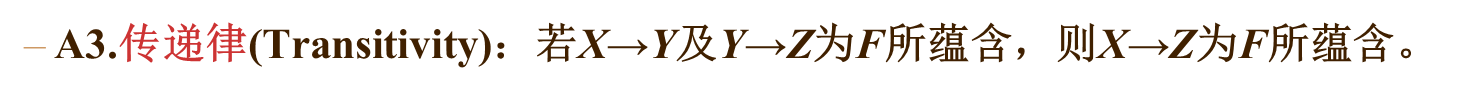
通俗的讲:
- 自反律:Y是X的子集,则X->Y
- 增广律:X->Y,则XZ->YZ
- 传递律:X->Y,Y->Z,则X->Z
直接看这几个公理挺让人一头雾水的,和之前一样,假设一个情景能更容易的理解这三条定律到底是在干嘛。
下面是一张完整的学生信息表
| 院系 | 专业 | 班级 | 姓名 | 性别 |
|---|---|---|---|---|
| 软件学院 | 软件工程 | 软工1901 | 张三 | 男 |
| 软件学院 | 信息安全 | 软信1902 | 赵四 | 女 |
| 软件学院 | 数字媒体技术 | 树莓1903 | 李六 | 男 |
| 以下为班级对应专业的表 | ||||
| 专业 | 班级 | |||
| :------------: | :------------: | |||
| 软件工程 | 软工1901 | |||
| 信息安全 | 软信1902 | |||
| 数字媒体技术 | 树莓1903 | |||
| 还有一张表,他的存在似乎用处不大,不过还是列一下 |
| 院系 | 专业 |
|---|---|
| 软件学院 | 软件工程 |
| 软件学院 | 信息安全 |
| 软件学院 | 数字媒体技术 |
1.自反律
最简单的例子,(软件学院,软件工程)这个属性组可以推出 软件工程 这个属性,这个性质完全就是废话,本身可以推出子集是一定满足的。
2.增广律
由专业和班级的对应表,软工1901 -> 软件工程
再加上张三这个名字,(软工1901,张三) -> (软件工程,张三),这个关系也是成立的
通过这种方式将函数依赖“增广”了,所以叫做增广律
3.传递律
传递律看上去更容易理解,比如:在确定这个学院里没有重名的人的情况下
有:软工1901->软件工程, 软件工程->软件学院
所以:软工1901->软件学院
以下给出正式证明:
1.自反律:
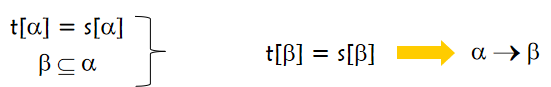
2.增广律
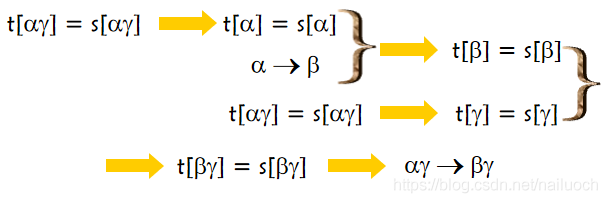
3.传递律
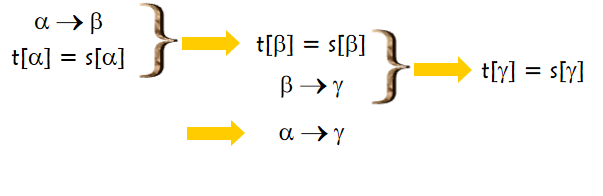
Armstrong公理的正确性和完备性:
- 正确性是指从F中推导出的函数依赖必为F所蕴含
- 完备性是指F所蕴含的所有函数依赖都可以从Armstrong公理中推导出
由以上三个公理可以推导出以下三条推理规则:
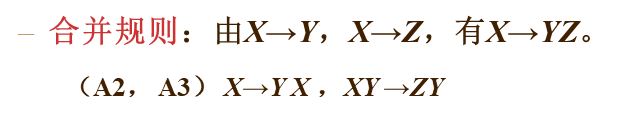
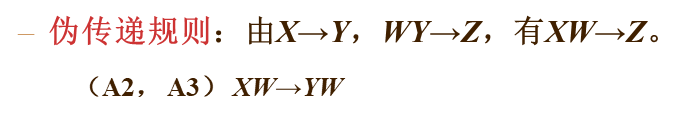
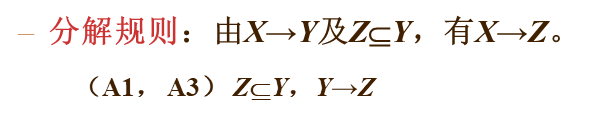
总结:
1.自反律(废话)
2.增广律
3.传递律
4.合并律 = 增广 + 传递
5.伪传递律 = 增广 + 传递(另一种用法)
6.分解律 = 自反 + 传递(也约等于废话)
参考文章1
参考文章2


 浙公网安备 33010602011771号
浙公网安备 33010602011771号