密码学的数学知识杂烩

记录一下如何解决转义字符问题

iv=input().encode()
iv = codecs.escape_decode(iv, "hex-escape")[0]

函数(摘自猫神博客

python

from pwn import * #引入pwn库
s=remote("",) #连接，两个参数好像叫post和host(来个好鸽鸽浇浇我罢),类似还有process用来连本地
s.send()#发送全部
s.sendline()#发送完后加上'\n'
s.recv(n) #接收nbit数据
s.recvline()#接收一行
s.recvuntil("")#接收到该字符串结束，以'\n'为标志
s.recvall()#全收了
s.close()#关闭

import string#在某些词频分析或者遍历的时候可以方便一点
string.ascii_letters()#英文字母，小写在前
string.ascii_lowercase()#小写字母
string.ascii_uppercase()#大写字母
string.digits()#0~9
string.hexdigits()/string.octdigits()#十六进制/八进制数
acsii.punctutation()#acsi符号 !"#$%&'()*+,-./:;<=>?@[\]^_`{|}~
string.printable()#可打印的字符

hashlib.sha256(buf.encode('utf-8')).hexdigest()#import hashlib

#没什么用的库，做一些迭代操作，一般只用到cycle来循环加密，不过既然要写就多写一点叭
import itertools 

#根据start和step生成一个自然数列表(本质上应该是生成器，但用法和列表是一样的，后面的函数也差不多)
counter=itertools.count(start,step) 

#把base的内容无限循
cycler=itertools.cycle(base) 

#无限循环element,如果times存在就重复times次
repeater=itortools.repeat(element,times) 

#根据截取无限序列的一部分，满足函数function时保留; 还有一个dropwhile函数与之相反
counter_part=itertools.takewhile(function,counter) 

#把a,b里面的元素合起来给s，好像没什么用
s=itertools.chain(a,b) 

#累积运算，默认是加法，初始值为0(乘法时是1)，每次和group的一个元素运算,结果添加到sum
sum=itertools.accumulate(group) 

#由group中所有 "长度为count并且没有重复元素" 的子集构成的集合;另有函数itertools.accumulate_with_replacement(),允许子集中有重复元素
itertools.combinations(group,count)

import gmpy2

#jacobi符号
j=gmpy2.jacobi(m,n)

sagemath

#生成矩阵  ZZ(QQ,GF(n)...)表示矩阵生成的基本环 ; list是矩阵元素组成的列表 ; a,b表示矩阵的行列（选填）
M=mtarix(ZZ[,a,b],list)

A = matrix(Zmod(p), A)
v = vector(Zmod(p), v)

#末尾添行
M=M.stack(vector(list)) 

#求秩
M.rank() 

#求行/列数
M.nrows() / M.ncols() 

#求值
M.determinant() / M.det()

#求逆
mt.is_invertible() #是否可逆
M.inverse()
M=M^(-1)

#转置
M=M.transpose()

#解方程
#Ax=B
x=A.solve_right(B)
#xA=B
x=A.solve_left(B)
#xA=0
x=A.left_kernel()
#Ax=0
x=A.right_kernel()
#格基规约
M=M.LLL()
M=M.BKZ()

#有限域

G1=GF(7,modulus='primitive') #用原本元生成域
G=GF(n) #定义了一个有限域G

a=G(k) #定义了G中的元素a(之后对a运算默认在G中)
x=a.nth_root(i) #求根 x^i=a(mod n),当i=2时可以用a.sqrt()
f=G.modulus() / x=G.gen() #生成模多项式和它的根(暂时不知道有什么用)

#整数环

r=Zmod(n) / r=Integer(n) #生成环

a=r(k) #定义环上的变量a
a=a^-1 #求逆
a=a.log(x) #求离散对数
a=a.sqrt() #求平方根
a.multiplicative_order() / a.additive_order() #求乘法/加法的阶

#多项式环

R.<x[,y,...]>=ZZ[] #定义整数多项式环，变量为x[,y,...]
R.<x>=Zmod(n)[] / R.<x>=GF(n)[] #定义有限域的多项式
R.<x>=PolynomialRing(Zmod(N)) / R=PolynomialRing(Zmod(N).'x') #定义有限域的多项式


f=R([c0,c1,...])/f=c0*x^i... #定义环上的多项式f
f.factor() #分解多项式
d=f.degree() #多项式的次数/度
f.gcd(g) / gcd(f,g) #欧几里得算法(xgcd同理)
f.roots() #求根，返回根值和重数
f.change_ring(R2) #更改多项式所在环

q2.resultant(q1) #求结式(对两个多元多项式消元的魔法)，仅在q1,q2定义在多变量环上使用

#扩展欧几里得算法
g,r,s=xgcd(a,b) #g=r*a+s*b

solve_mod(equations, modulus) #equation=[f1,f2]

#分解质因数
factor(20) #2^2*5
prime_divisors(20) #[2,5]
p,q=qsieve(n)[0] #二次筛法，可分解大致200位的n
p,q=ecm.factor(n) #GMP-ECM算法

#中国剩余定理
x=crt(res,mod)

#欧拉函数
phi=euler_phi(n)

#模逆
x=inverse_mod(a,n)
x=power_mod(a,-1,n)

#取整
#向上取整
x=x.ceil()
x=ceil(x)
#向下取整
x=floor(X)
x=x.floor()

#离散对数
#如果在有限域上运算可以省略其中的mod
x=discrete_log(mod(y,n),mod(g,n)) #y=g^x(mod n)
x=discrete_log_rho(mod(y,n),mod(g,n))#Pollard-Rho算法

二次剩余求解:

from random import *


def legendre(a, p):
    symbol = pow(a, (p - 1) // 2, p)
    if symbol == p - 1:
        return -1
    return symbol


def tonelli(a, p):
    if a == 0 or legendre(a, p) != 1:
        return 0
    q = p - 1
    s = 0
    while q % 2 == 0:
        q //= 2
        s += 1
    if s == 1:
        return pow(a, (p + 1) // 4, p)

    z = 2
    while legendre(z, p) != -1:
        z += 1

    m = s
    c = pow(z, q, p)
    t = pow(a, q, p)
    r = pow(a, (q + 1) // 2, p)

    while t != 1:
        t2 = t
        i = 0
        while t2 != 1 and i < m:
            t2 = pow(t2, 2, p)
            i += 1
        b = pow(c, 2 ** (m - i - 1), p)
        m = i
        c = (b * b) % p
        t = (t * c) % p
        r = (r * b) % p

    return r


#x^2=c mod p
def Cipolla_algorithm(c,p):                                              #solve2
    # 定义模p复数域上的乘法
    def multiplication(x1,y1,x2,y2,w,p):
        x=(x1*x2+y1*y2*w)%p
        y=(x1*y2+x2*y1)%p
        return x,y

    # 获取w,使得w=-1mod(p),w是复数元的平方
    def get_w(c,p):
        a=randint(1,p)
        w=pow(a, 2) - c
        while pow(w,(p - 1)//2,p)!=p-1:
            a=randint(1,p)
            w=pow(a,2)-c
        return w,a
    #主体部分
    w,a=get_w(c,p)
    power=(p+1)//2
    x1=a
    y1=1
    x=1
    y=0

    while(power!=0):
        if(power!=(p+1)//2):
            x1,y1=multiplication(x1,y1,x1,y1,w,p)
        if(power & 1):
            x,y=multiplication(x,y,x1,y1,w,p)
        power>>=1
    return x


print(tonelli(4,13))

print(Cipolla_algorithm(4,13))

连分数（作除近似爆破）

c = continued_fraction(e/n)
for i in range(2,len(c)):
    k = c.numerator(i)
    d = c.denominator(i)

paillier cryptosystem

LLL learning

LLL算法规约出来的向量要求

经典的闵可夫斯基界

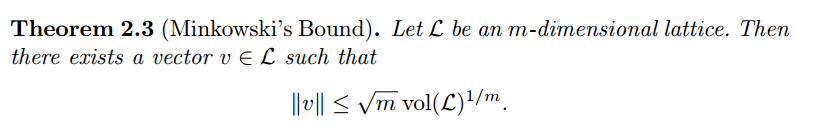
目标向量不平衡 :

if the components of the target vector are not balanced we can multiply the equation by an appropriate diagonal matrix to construct a new lattice and target vector.

X. Y, Z are the boundaries of x, y, and z

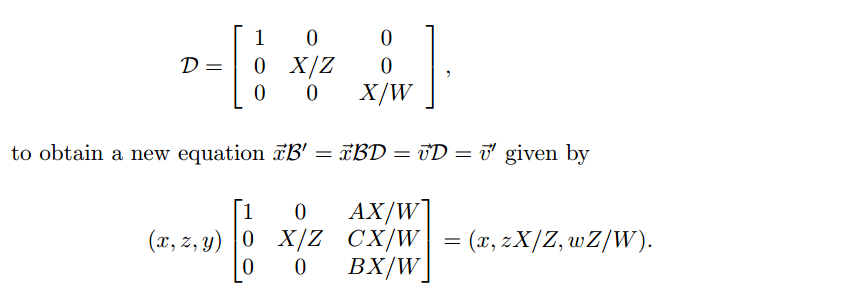
规约出来第一个向量的性质

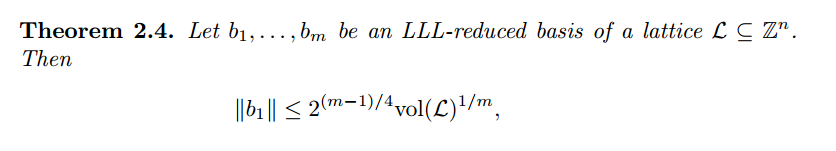
例子:

对于k*(q+r)+s =2^{1024}p

我们有以下式子

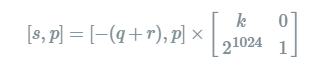
1 import gmpy2
2 k=94541588860584895585135152950569493777168309607384495730944110393788712443252059813470464503558980161423182930915955597122997950103392684040352673659694990925903156093591505153081718027169554019948988048641061593654540898258994671824807628660558123733006209479395447337793897155523508261277918178756662618785
3 A=Matrix([[k,0],[2**1024,1]])
4 print(A.LLL()[0])
5 A=Matrix([[1,2**1024],[0,k]])
6 print(A.LLL()[0])

可以知道[s,p]是由格A经过一系列变换得到的，因此该向量存在于格A所在的格子

由闵可夫斯基界我们可以得知最小向量的模长小于(2*k)^1/2

如果能规约出[s,p]则p**2+s**2<2*k,p,s为512位,k为1024位。

通过测试发现对于随机生成的三个数,上面等式大约0.8的概率成立.也就是目标向量大概率是最短向量

所以我们可以通过LLL规约出最小向量[s,p]

如果是第二种矩阵的构造方式，规约出的最小向量为[-p,-s]

格子中最小向量有v，-v所以规约出来的可能与预期不同，但只要调整一下正负便可。

Coppersmith learning

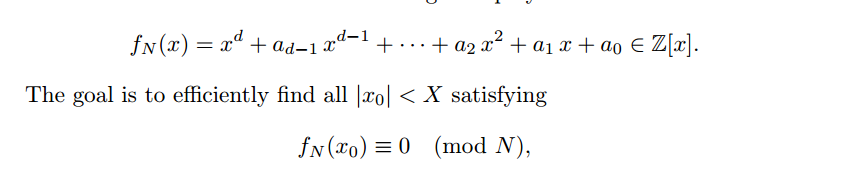
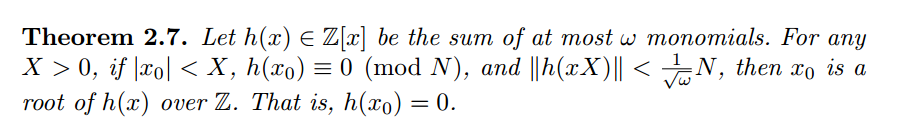
m高位泄露

可以构造格子如下:

我们预期要找到在整数环下的多项式来求解m，也就是说这样的多项式模长肯定比N要小。

由于格中最短向量为[0,0,0,N],因此是可以规约出来的。

那么现在思考一下m的未知位最大界限(也就是M)是多少呢？

由闵可夫斯基界并忽略其常数部分可以推算得到

M<N^(1/6) （当然这个界肯定可以扩大，通过升维的方式

如果M稍大于上界，我们可以爆破一些位，来更好的规约出目标多项式。

N =
e =
c =
m =

ZmodN = Zmod(N)
P.<x> = PolynomialRing(ZmodN)
f = (m + x)^e - c
x0 = f.small_roots(X=2^kbits, beta=0.4)[0]  
print("m:", m + x0)

p高位泄露

对于p0+x我们有以下格子(R为p的上界

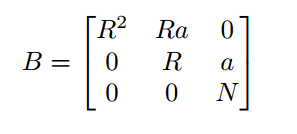
B的每一行向量都具有模p的性质

我们目标向量在模n下有(k1*R^2 , (k1*a+k2)R , k2*a)

由于格B中的最短向量是（0，0，0，N）所以符合我们要寻找整数环下多项式的原则

由闵可夫斯基界并忽略其常数部分可以推算得到

R<p^(1/3)≈N^(1/6) （可以通过插入有关f和N的多项式来扩大格子的维度大约扩大到p的一半差不多

1 PR.<x>=PolynomialRing(Zmod(N))
2 f=p0+x
3 f=f.monic()
4 roots=f.small_roots(X=2**1000,beta=0.4)
5 x0=roots[0]

from Crypto.Util.number import *

p=getPrime(512)
q=getPrime(512)
n=p*q
p0=p>>100<<100


R=2**100
B=[
    [R**2,R*p0,0],
    [0,R,p0],
    [0,0,n]
]

B=matrix(B)
a3,a2,a1=B.LLL()[0]
a3=a3//R**2
a2=a2//R
a1=a1

polZ.<x> =PolynomialRing(ZZ)
f=a3*x**2+a2*x+a1
roots =f.roots()[0][0]
print(p0+roots==p)  #True

#p低位泄露和p高位泄露差不多，就不多说了。

p中间连续bit位泄露

对于f = x+2^t*y+a 我们有以下格子（R为x和y的上界

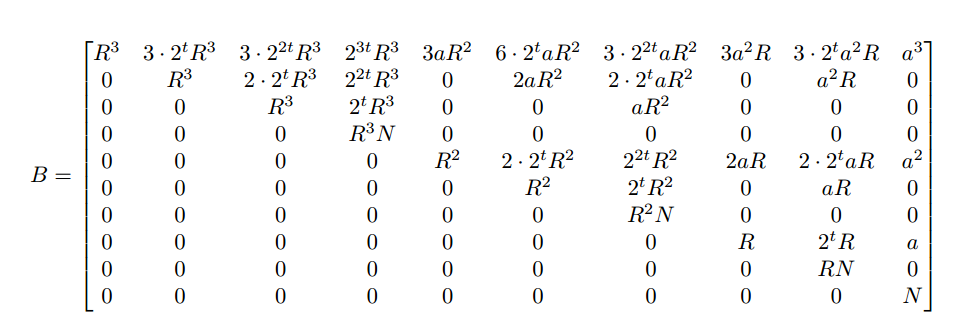
由于是二元函数，所以至少需要2个多项式，因此对格的体积还是有要求的。

我们的格子是基于下面多项式而构造的

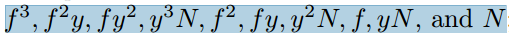
经过LLL规约出来的两个最短向量可能不是独立的，所以我们有时也会用到第三个规约出来的向量。

对于上述式子我们可以解方程或者使用Gr¨obner basis来找到公共根

下面我们来分析一下R的最大限制是多少

det B =R^20*N^4

由闵可夫斯基界并忽略其常数部分可以推算得到

R^20<N (p≈N^(1/2))

from sage.all import *
from sage.matrix.constructor import random_matrix
from Crypto.Util.number import *
import gmpy2

#根据给定系数和自变量列表构造多元多项式
def gen_function(coe_list,var_list):
    assert len(coe_list)==len(var_list)
    f=0
    for i in range(len(coe_list)):
        f+=coe_list[i]*var_list[i]
    return f
#根据多项式、自变量上界、自变量列表构造格
def gen_matrix(f_list,upper_list,var_list):
    assert len(f_list)==len(var_list)==len(upper_list)
    s=gen_function([1]*len(var_list),var_list)
    L=[]
    for i in range(len(f_list)):
        cc=(f_list[i]+s).coefficients()
        coe=[(cc[_]-1)*upper_list[_] for _ in range(len(cc))]
        L.append(coe)
    return matrix(L)
def RSA_middle_bits_of_p(X,Y,N,p0,bits):
    PRxy.<x,y> = PolynomialRing(ZZ)
    f=x+(2^bits)*y+p0
    variable=[x^3,x^2*y,x*y^2,y^3,x^2,x*y,y^2,x,y,1]
    f_list=[f^3,f^2*y,f*y^2,y^3*N,f^2,f*y,y^2*N,f,N*y,N]
    upper_list=[X^3,X^2*Y,X*Y^2,Y^3,X^2,X*Y,Y^2,X,Y,1]
    #格构造及规约
    L=gen_matrix(f_list,upper_list,variable)
    LLL=L.LLL()
    Coefficient=[]
    #将约化基还原成系数矩阵
    for i in range(len(f_list)):
        Coefficient.append([int(LLL[i][j])//upper_list[j] for j in range(len(list(LLL[i])))])
      #取出两组系数矩阵构造二元方程组，其范数小于p
    h=gen_function(Coefficient[0],variable)
    g=gen_function(Coefficient[6],variable)
    #取结式消元
    q=h.resultant(g)
    assert q!=0,"两个方程不互素,请重新选择向量"
    q=q.univariate_polynomial()
    PRx.<xn>=PolynomialRing(ZZ)
    q=q.change_ring(PRx).subs(y=xn)
    q=q.monic()
    #求取结式的根即为y
    roots=q.roots()
    assert roots,"No roots found"
    res_y=int(roots[0][0])
    #将Y回代入上述方程之一，再解一元方程即得x
    g=eval(str(g).replace('y','res_y').replace('^','**'))
    g=g.change_ring(PRx).subs(x=xn)
    res_x=g.roots()[0][0]
    p=int(f(res_x,res_y))
    q=N//p
    assert p*q==N,"error"
    print("p={}\nq={}".format(p,q))
    return p,q


p=getPrime(1024)
q=getPrime(1024)
n=p*q
p=(p<<8)>>16
p0=p<<8
t=2**(1024-8)
R=2**8
B=[]
v=[]
y=t*R
f=R+t*R+p0
p,q=RSA_middle_bits_of_p(2**8,2**8,n,p0,8)
print(p*q==n)
#True

dp高位泄露

我们有以下式子 e(d0+x)+kp-1 = 0 mod p (由于kp小于e 可以爆破）

由上式我们有如下格子(R为e*x的上界 A=e*d0+kp-1

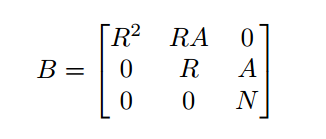
其实格子和之前的p高位差不多这边就不细讲了