NewStarCTF An der schönen Elliptische Kurve题解

from secret import FLAG, ECDH_KEY_EXCHANGE
from Crypto.Cipher import AES
from hashlib import md5
from os import urandom

iv = urandom(16)


a = 14489
b = 10289
p = 7486573182795736771889604737751889118967735916352298289975055815020934891723453392369540853603360270847848895677903334441530052977221688450741083448029661

F = GF(p)
E = EllipticCurve(F, [a, b])

G = E.random_point()

my_private_key = random_prime(2^256)

shared, sender_public_key = ECDH_KEY_EXCHANGE(G, my_private_key)

key = md5(str(int(shared.xy()[0])).encode()).digest()

cipher = AES.new(key, AES.MODE_CBC, iv)
ciphretext = cipher.encrypt(FLAG)

print(a)
print(b)
print(p)
print(sender_public_key)
print(my_private_key)
print(ciphretext.hex())
print(iv.hex())

#

14489
10289
7486573182795736771889604737751889118967735916352298289975055815020934891723453392369540853603360270847848895677903334441530052977221688450741083448029661
(1285788649714386836892440333012889444698233333809489364474616947934542770724999997145538088456652601147045234490019282952264340541239682982255115303711207 : 1081635450946385063319483423983665253792071829707039194609541132041775615770167048603029155228167113450196436786905820356216200242445665942628721193713459 : 1)
2549545681219766023689977461986014915946503806253877534915175093306317852773
2f65ff4a97e0e05c06eab06b58ea38a3d5b6d2a65ea4907bc46493b30081a211d7cffc872a23dbd565ef307f9492bb23
d151c04c645c3e2a8d3f1ae44589ef20

#

下面先给出ECDH密钥交换算法

假设密钥交换双方为Alice、Bob，其有共享曲线参数（椭圆曲线E、阶N、基点G）。

1) Alice生成随机整数a，计算A=a*G。 #生成Alice公钥

2) Bob生成随机整数b，计算B=b*G。 #生产Bob公钥

3) Alice将A传递给Bob。A的传递可以公开，即攻击者可以获取A。

    由于椭圆曲线的离散对数问题是难题，所以攻击者不可以通过A、G计算出a。

4) Bob将B传递给Alice。同理，B的传递可以公开。

5) Bob收到Alice传递的A，计算Q =b*A  #Bob通过自己的私钥和Alice的公钥得到对称密钥Q

6) Alice收到Bob传递的B，计算Q`=a*B  #Alice通过自己的私钥和Bob的公钥得到对称密钥Q'

Alice、Bob双方即得Q=b*A=b*(a*G)=(b*a)*G=(a*b)*G=a*(b*G)=a*B=Q' (交换律和结合律)，即双方得到一致的密钥Q。

那么我们本题的突破点就是求出shared

由ECDH交换算法可以得出shared=sender_public_key*my_private_key

得出shared后则是进行AES解密求出flag

下面给出解题脚本（sagemath真滴香）

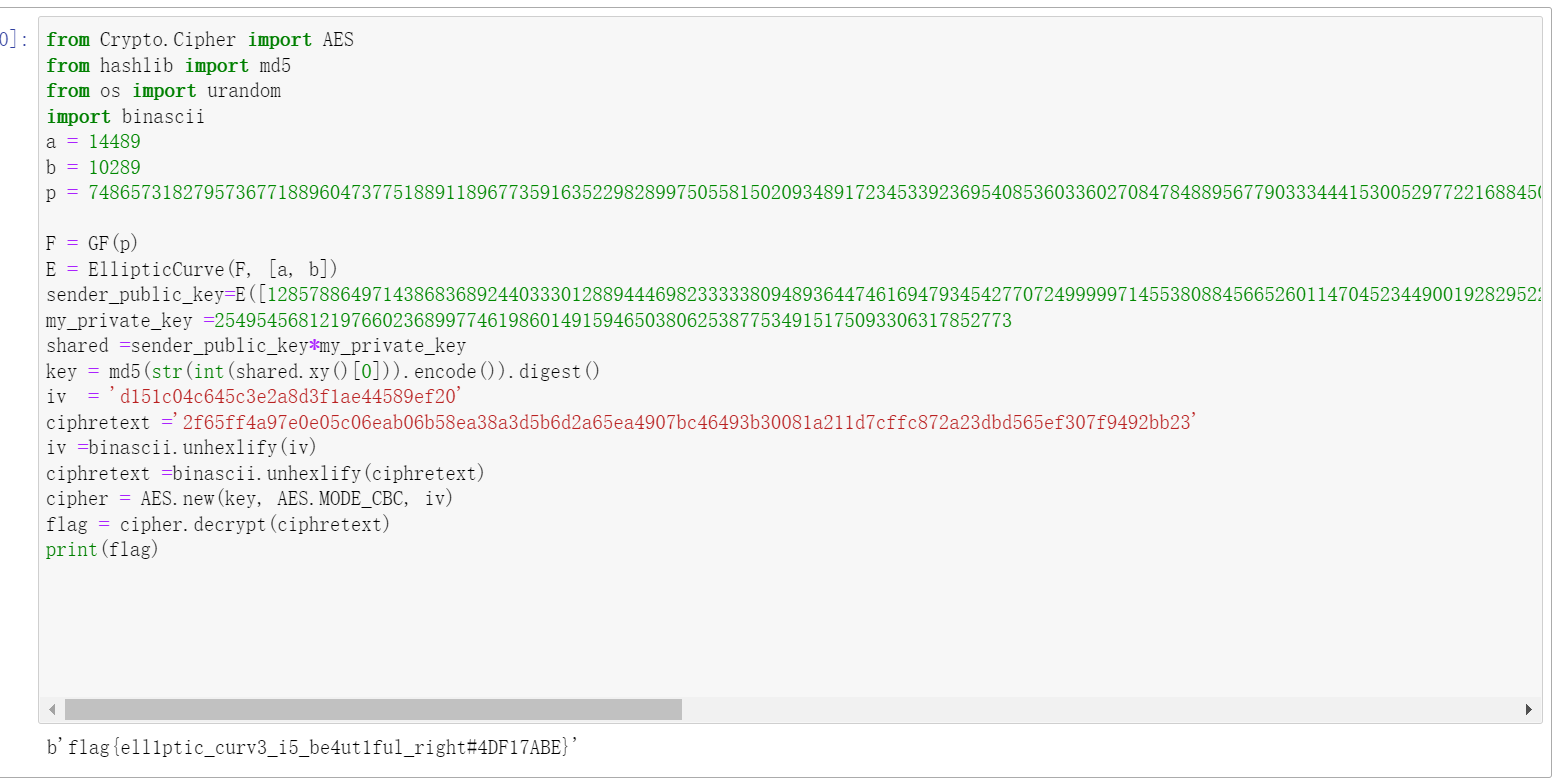
from Crypto.Cipher import AESfrom hashlib import md5
from os import urandomimport binascii
#用sagemath运行代码
a = 14489
b = 10289
p =74865731827957367718896047377518891189677359163522982899750558150209348917234533923695408536033602708478488956779033
F= GF(p)
E=EllipticCurve(F,[a,b])
sender_public_key=E([1285788649714386836894403330128894446982333380948936447461694793454277072499999714553808845665260my_private_key =2549545681219766023689977461986014915946503806253877534915175093306317852773
shared =sender_public_key*my_private_key
key = md5(str(int(shared.xy () [o]) ).encode()).digest ()
iv = 'd151c04c645c3e2a8d3f1ae44589ef2o'
ciphretext ='2f65ff4a97eOe05c0Geab06b58ea38a3d5b6d2a65ea4907bc46493630081a211d7cffc872a23dbd565ef307f9492bb23'
iv =binascii.unhexlify(iv)
ciphretext =binascii.unhexlify(ciphretext)cipher = AES.new(key，AES.MODE_CBC,iv)flag = cipher.decrypt(ciphretext)
print(flag)

 

 新生赛收尾之题 结束