树状数组笔记整理

树状数组介绍

树状数组，顾名思义，就是树状的一维数组。

二叉树同样也可以用一维数组存储。我们以二叉树进行类比。

如图所示，图中节点的序号就是存在数组中的下标。

记父节点序号为 $p$ ,子节点序号为 $s$ 。

则有:

$p$ $=$ $s$ $/$ $2$ (向下取整)。

左子节点 $s_{left}$ $=$ $p$ $* 2$ 。

右子节点 $s_{right}$ $=$ $p$ $*2+1$ 。

综上可知，二叉树能用一维数组存，是由于其父子节点间存在一定关系，以至于不需要用额外的变量来表示信息。

那类比到树状数组中，可以发现：

$c$ 数组即为树状数组。 $c_i$ 表示区间 $a$ $[i-lowbit(i),i]$ 的和。

ps：点我了解lowbit运算是什么

同样记父节点下标为 $p$ ,子节点下标为 $s$ 。

则有：

$p$ $=$ $s$ $+$ $lowbit(s)$ 。

由这条公式亦可反推出：

$s$ $=$ $p$ $-$ $2^i$ ( $0 \le i < p_{last}$ )

这里的 $p_{last}$ 指的是 $p$ 二进制表示下最后一位 $1$ 所在的位数。

例如： $6$ 的二进制数表示为 $110$ ,则它的 $p_{last}$ 为 $1$ 。（这里的位数从右往左从 $0$ 开始记）。

因为公式 $1$ 由 $s$ 加上自身 $lowbit(s)$ 得到 $p$ 其过程一定会产生进位。且 $lowbit(s)$ 一定小于 $lowbit(p)$ ,所以可以倒推得到子节点。

由于以上关系，树状数组不仅可以用一维数组存。而且还衍生出了一系列用途。

树状数组功能

单点增加

Q：给序列中的一个数 $a[x]$ 加上 $y$ 。此时如何维护树状数组？

A:将所有包含 $a[x]$ 的节点加上 $y$ 即可，也就是 $c[x]$ 和它所有的祖先节点。

ps:初始化时亦可运用此操作。

点击查看代码

 void add(int x,int y){
	for (; x <= N;x += x&-x)  c[x] += y;
	return ;
}

动态维护前缀和

之所以说动态维护，因为用树状数组维护前缀和只需要 $\log N$ 的时间复杂度。更为优秀。

Q：求 $a$ 数组 $a_i \sim a_x$ 的和。

A：将数 $x$ 分成若干个区间。

区间共同特点：若区间结尾为 $R$ ，则区间长度就等于 $lowbit（R）$ ，即 $R$ 二进制分解下最小的整数次幂。

举例：当 $x$ = $7$ 时

如图所示。

区间划分方式与树状数组相同。前面又提到“ $c$ 数组即为树状数组。 $c_i$ 表示区间 $a$ $[i-lowbit(i),i]$ 的和。”

因此只需要将这几个区间所对应的 $c_i$ 相加。即可得到前缀和。

点击查看代码

 int ask(int x){
	int ans = 0;
	for (; x ; x -= x & -x) ans += c[x];
	return ans;
}

例题【具体应用】

主要利用树状数组可以快速求前缀和的优势，以数据范围为下标，快速统计区间内的个数（或所需要的信息），适用于数据范围适中（一般为 $0 \le x \le 10^6$ ）且需要多次求前缀和的题目。

【例题1】三元上升子序列

【题目分析】

对于一个数 $x$ ,计算其作为 $j$ 时，位置在它前面比它小的数 $x_{min}$ 、位置在它后面比它大的数 $x_{max}$ ,运用乘法原理的知识可知，将 $x_{min} \times x_{max}$ ,即可得到 $x$ 作为 $j$ 时的方案数，枚举所有 $x$ ,即可得到总方案数。

【树状数组作用】

统计 $x_{min}$ 和 $x_{max}$ 时，即可将数 $x$ 的范围作为树状数组的下标。

此时两种操作所代表的意思分别为：

$add(x,1)$ 表示数值为 $x$ 的数的个数 $+1$ 。

$sum(y)$ 表示在已经扫描过的区间内，数值为从 $1 \sim y$ 的所有数的个数。

顺序扫描序列，对于数 $x$ ,统计两个信息。

$r_{i,0}$ 表示位置在数 $x$ 前面，且比它小的数。

$r_{i,1}$ 表示位置在数 $x$ 前面，且比它大的数。

位置在数 $x$ 后面，且比数 $x$ 大的数就等于：

$所有数 - 所有位置在 x 前面比 x 小的数 - r{i,1}$ 。

【code】

点击查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
#define ll long long
using namespace std;
ll tree[100005],n,num;
ll r[40005][2],a[100005];
void add(ll x,ll y){
	for(;x<=100005;x+=(x&-x)) tree[x]+=y;
}
ll sum(ll x){
	ll ans=0;
	for(;x;x-=(x&-x)) ans+=tree[x];
	return ans;
}
int main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		ll x;
		scanf("%lld",&x);
		a[i]=x;
		num=max(num,x);
		add(x,1);
		r[i][0]=sum(x-1);
		r[i][1]=sum(num)-sum(x);
	}
	ll ans=0;
	for(int i=1;i<=n;i++)
		ans+=r[i][0]*(sum(num)-sum(a[i])-r[i][1]);
	cout<<ans<<endl;
	return 0;
}

【summary】

此题算是初步认识了以数值范围为下标的树状数组的用法。下一大点求逆序对的思想与此相同。

【例题2】 [USACO04OPEN] MooFest G 加强版

【题目分析】

将奶牛按照音量从小到大进行排序，保证当前奶牛的音量一定最大，然后分类讨论所有比当前奶牛音量小的奶牛与当前奶牛的距离(坐标比当前奶牛大的和坐标比当前奶牛小的)。两者相加，乘上当前奶牛音量，枚举每个奶牛，即可得到答案。

【树状数组作用】

定义两个树状数组，都是以距离的范围作为下标， $c$ 数组用于统计对应距离的个数， $t$ 数组用于表示对应距离 $\times$ 对应距离个数的总数，通过二者，即可快速计算距离差。

【code】

计算过程的解释已在代码中注释出来。

点击查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
ll n,t[50005],c[50005];
struct A{
	ll v,x;
}a[50005];
bool cmp(A xx,A yy){
	if(xx.v==yy.v) return xx.x<yy.x;
	return xx.v<yy.v; 
}
void addc(ll x,ll y){
	for(;x<=50000;x+=(x&-x)) c[x]+=y;
}
void addt(ll x,ll y){
	for(;x<=50000;x+=(x&-x)) t[x]+=y;
}
ll sumc(ll x){
	ll sum=0;
	for(;x;x-=(x&-x)) sum+=c[x];
	return sum;
}
ll sumt(ll x){
	ll sum=0;
	for(;x;x-=(x&-x)) sum+=t[x];
	return sum;
}
int main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].v,&a[i].x);
	sort(a+1,a+n+1,cmp); 
	ll ans=0,max_num=0;
	for(int i=1;i<=n;i++){
		max_num=max(max_num,a[i].x);
		//以下距离之间的比较限于所有音量比当前奶牛小的奶牛。
		//a[i].x*sumc(a[i].x-1) 表示当前奶牛的距离*距离比当前奶牛小的奶牛个数。
		//sumt(a[i].x-1) 表示所有距离比当前奶牛小的奶牛的距离和。
		//sumt(max_num)-sumt(a[i].x) 表示所有距离比当前奶牛大的奶牛的距离之和。
		//sumc(max_num)-sumc(a[i].x))*a[i].x 表示当前奶牛距离 * 距离比当前奶牛大的奶牛个数
		ans+=a[i].v*(a[i].x*sumc(a[i].x-1)-sumt(a[i].x-1)+(sumt(max_num)-sumt(a[i].x))-(sumc(max_num)-sumc(a[i].x))*a[i].x) ;
		addc(a[i].x,1);
		addt(a[i].x,a[i].x);
	}
	cout<<ans<<endl;
	return 0;
}

【summary】

这一题的重点给到题目中树状数组 $t$ 。主要收获为：以数值范围为下标的树状数组，能够处理的信息不仅限于个数。

【例题3】P1972 [SDOI2009] HH的项链

【题意分析】

本题核心：如何判断一个区间内的贝壳是否重复？

当右端点 $r$ 固定时，不论 $l$ 取何值，对于任意一组重复的贝壳，都可以只统计最右端的贝壳。

原因：设一组重复贝壳中最右端的贝壳所在的位置为，那么当时，其他贝壳也不可能算进统计中，当 $pos_r \ge l$ 时，无论其他贝壳是否被包括，对于区间的贡献都只有 $1$ ，因此，只计算最右端的贝壳即可。

因此，只需要将所有询问区间按 $r$ 从小到大排序，计算答案即可。

【树状数组作用】

以位置为下标，每遇到一个新的数 $num(num \le r)$ ，判断它是否重复，如果重复，那么将上一个相同的数的贡献值 $-1$ ，将当前数的贡献值 $+1$ 。

对于一段区间 $[l,r]$ ，答案为 $sum(r)-sum(l-1)$ 。

【code】

点击查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int n,m,ask_r,prev,pos;
int vis[1000005],a[1000005],t[1000005],ans[1000005];
struct A{
	int l,r,num;
}ask[1000005];
bool cmp(A x,A y){
	return x.r<y.r;
}
int find(int pos){
	ask_r=ask[pos++].r;
	while(ask_r==ask[pos].r) pos++;
	return pos-1;
}
void add(int x,int y){
	for(;x<=n;x+=(x&-x)) t[x]+=y;
	return;
} 
int sum(int x){
	int su=0;
	for(;x;x-=(x&-x)) su+=t[x];
	return su;
}
void replace(){
	for(int i=ask[prev].r+1;i<=ask_r;i++){
		if(vis[a[i]]!=0) add(vis[a[i]],-1);
		add(i,1);
		vis[a[i]]=i;
	}
	for(int i=prev+1;i<=pos;i++) ans[ask[i].num]=sum(ask[i].r)-sum(ask[i].l-1);
	return;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	scanf("%d",&m);
	for(int i=1;i<=m;i++) scanf("%d%d",&ask[i].l,&ask[i].r),ask[i].num=i;
	sort(ask+1,ask+m+1,cmp);
	while(1){
		if(pos==m) break;
		prev=pos;
		pos=find(pos+1);
		replace();
	}
	for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
	return 0;
}

【 $summary$ 】

此题不再以数据范围为下标，而是以位置为下标。对于树状数组的应用更加灵活。在想到以最右端的贝壳为有价值的贡献时，对应到树状数组的操作就可以是上一个重复的数的贡献值 $-1$ ，当前数的贡献值 $+1$ 。然后用前缀和统计区间内的个数。算进一步的开阔思维。

例题3 update P2184 贪婪大陆

与例题三不同，这一题给出的并不是一串，而是一个区间一个区间的给，但求得同样都是某一区间内贝壳的种类数。

【思路分析】

容易发现对于给定的区间，求与其有交集的区间的个数。将 $L$ 记为区间头， $R$ 记为区间尾， $L$ 一定在给定区间的 $R$ (包含 $R$ )的前面，但不被给定区间包含的区间， $R$ 一定在给定区间的 $L$ (不包含 $L$ )的前面。

因此只需要用两个树状数组统计头尾，用 $R$ 以前所有的头减去 $L$ 以前所有的尾即可。

【code】

点击查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n,m,q;
int h[100005],t[100005];
void add(int *a,int x){
	for(;x<=n;x+=(x&-x)) a[x]+=1;
	return;
}
int sum(int *a,int x){
	int cnt=0;
	for(;x;x-=(x&-x)) cnt+=a[x];
	return cnt;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d",&q);
		int l,r;
		if(q==1){
			scanf("%d%d",&l,&r);
			add(h,l);
			add(t,r);
		}
		else{
			scanf("%d%d",&l,&r);
			cout<<sum(h,r)-sum(t,l-1)<<endl;
		}
	}
	return 0;
}

求逆序对

本质上也是通过树状数组单点增加和区间求和的操作进行计算。作为一个专题单独列出来。

桶排+树状数组：

1.桶排部分：

对于一个序列 $a$ , 我们建立一个 $cnt$ 数组， $cnt[x]$ 表示 $x$ 在序列 $a$ 中出现过的次数。当 $a_i=val$ 时， $cnt[val]++$ 。

2.树状数组部分：

倒序扫描序列 $a$ ，对于新加入的数 $a_i$ ，查询 $cnt[1~a_i-1]$ 的前缀和，并将返回的前缀和加入答案。前缀和部分就可以用树状数组来维护。

操作简单粗暴，但相当好用。

点击查看代码

 for ( int i = n; i; i --) {
	ans += ask (a[i] - 1);
	add (a[i] , 1 );
}

【例题】

接下来通过三道题进一步了解一下逆序对的考法。（不做一下真没想到还能这样考。）

【例题1】P2448 无尽的生命

【题意简述】

看到题目显而易见是求逆序对个数。

【思路分析】

看到数据范围 $x_i,y_i \le 2^{31}-1$ ， $k \le 10^5$ 。数据值域大但是个数少，且与数据之间的大小关系有关，因此考虑离散化。

离散化简单介绍

离散化实际就是一种映射，当数据值域过大而个数有限时，可以尝试离散化。

具体过程以此题为例。假设给出这么一组数据

 2
 
123456789 123456
 
987654321 123456

首先将所有出现过的数收集起来，存进 $a$ 数组，并进行排序，然后再去重保存进 $pos$ 数组当中。

接下来就可以建立映射关系。将数值大的数在 $num$ 数组中用数值小的数代替，但各个数之间的大小关系不变，接下来交换操作先用二分答案在 $pos$ 数组中检索，然后通过映射在 $num$ 数组中进行交换。

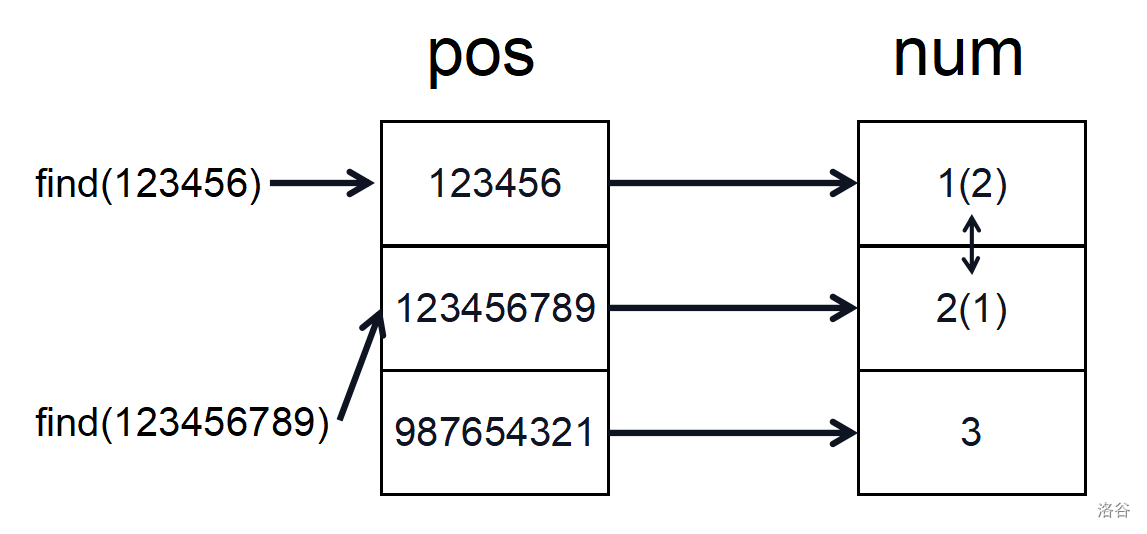
最终被交换过的数之间的逆序对在 $num$ 数组中求即可。

被交换的数与未被交换的数之间的逆序对

考虑每个被交换的数对答案的贡献。

设 $x<y$ ,当 $x$ 和 $y$ 交换后。

对于 $x$ 来说, $x \sim y$ 之间所有未被交换的数都比 $x$ 大，形成逆序对。

对于 $y$ 来说， $x \sim y$ 之间所有未被交换的数都比 $y$ 小，形成逆序对。

逆序对个数都为 $x \sim y$ 之间所有未被交换的数。

温馨提示：以下主要为代码实现讲解，本质思想同上。

对于交换过后的 $num$ 数组， $num_i$ 表示的是位置 $pos_i$ 上当前所在的数在 $num$ 数组中对应的数。记数 $x$ 为位置 $pos_i$ 上当前所在的数。

$pos_{num_i}$ 表示数 $x$ 现在所在的位置。

$pos_i$ 表示数 $x$ 原来在的位置。

$\left\vert pos_i-pos_{num_i}-1\right\vert$ 表示两个位置间所有的数。

$\left\vert num_i-i-1\right\vert$ 表示两个位置间所有被交换过的数。

因此所有未被交换的数就为 $\left\vert pos_i-pos_{num_i}-1\right\vert - \left\vert num_i-i-1\right\vert$ 。

【code】

点击查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
struct A{
	int x,y;
}a[100005];
int k,pos[200005],num[200005],cnt,len;
int t[100005];
void add(int x){
	for(;x<=len;x+=(x&-x)) t[x]+=1;
}
long long sum(int x){
	long long ans=0;
	for(;x;x-=(x&-x)) ans+=t[x];
	return ans;
}
int find(int x){
	int l=1,r=len;
	while(l<r){
		int mid=(l+r)>>1;
		if(pos[mid]<x) l=mid+1;
		else if(pos[mid]>x) r=mid-1;
		else return mid;
	}
} 
int main(){
	scanf("%d",&k);
	for(int i=1;i<=k;i++){
		scanf("%d%d",&a[i].x,&a[i].y);
		num[++cnt]=a[i].x;
		num[++cnt]=a[i].y;
	}
	sort(num+1,num+cnt+1);
	for(int i=1;i<=cnt;i++){
		if(num[i]==num[i-1]) continue;
		pos[++len]=num[i];
	}
	for(int i=1;i<=len;i++) num[i]=i;
	for(int i=1;i<=k;i++){
		int pos1=find(a[i].x);
		int pos2=find(a[i].y);
		swap(num[pos1],num[pos2]);
	}
	long long ans=0;
	for(int i=len;i>=1;i--){
		add(num[i]);
		ans+=sum(num[i]-1);
		ans+=abs(pos[num[i]]-pos[i]-1)-abs(num[i]-i-1); 
	} 
	cout<<ans<<endl;
	return 0;
}

【summary】

重点在于与未交换的数之间的求解。题目中序列的长度可以长到一个数组都存不下，但却可以用公式求呢。

【例题2】P3531 [POI2012]LIT-Letters

【题目描述】

该题的重点在于如何从题面描述转到求 $逆序对$ 。抓到重点：

交换 $a$ 中相邻两个字符，求最少的交换次数。
$a,b$ 中只含大写字母，且数据保证 $a$ 可以变成 $b$ 。

对 $b$ 串中的字符进行顺序编号（假设此时 $b$ 中并没有重复的字母），并对应到 $a$ 串中。

例如：

 3
ABC
BCA

对 $BCA$ 进行顺序编号，对应到 $ABC$ 就是 $312$ 。

当序列中存在数，满足 $pos_a < pos_b$ , $a > b$ 。也就是形成逆序对。

而对于我们的目标，将 $a$ 串变成 $b$ 串，需满足任意数 $a , b$ ，都有 $pos_a < pos_b$ , $a < b$ 。

显然我们需要通过一定操作，令逆序对都消失，以达到目标。

由于题目中的交换为交换相邻的数，因此只要 $a$ 与 $b$ 不交换，它们之间的相对位置就不会变，也就不能达成目标。

综上所述，最少的交换次数就是逆序对的个数。

当字母重复时，我们要如何让编号对应到 $a$ 呢？

显然逆序对个数越少越好，因此对于相同的字母，按出现的顺序进行顺序编号。代码中用单向链表实现。

【code】

点击查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#define ll long long
using namespace std;
int now[30],prev[30],nex[1000005];
char s[1000005],ss[1000005];
int a[1000005],t[1000005],lens;
void add(int x,int y){
	for(;x<=lens;x+=(x&-x)) t[x]+=y;
	return;
}
ll sum(int x){
	ll ans=0;
	for(;x;x-=(x&-x)) ans+=t[x];
	return ans;
}
int main(){
	scanf("%d",&lens);
	cin>>(s+1);
	cin>>(ss+1);
	for(int i=1;i<=lens;i++){
		int ch=s[i]-'A';
		if(now[ch]==0) now[ch]=i;
		nex[prev[ch]]=i;
		prev[ch]=i;
	}
	for(int i=1;i<=lens;i++){
		int ch=ss[i]-'A';
		a[now[ch]]=i;
		now[ch]=nex[now[ch]];
	}
	ll ans=0;
	for(int i=lens;i>=1;i--){
		add(a[i],1);
		ans+=sum(a[i]-1);
	}
	cout<<ans<<endl;
	return 0;
}

【例题3】P6186 [NOI Online #1 提高组] 冒泡排序

【思路剖析】

主要难点在于查询操作。

 5 4 2 3 6 1
 
4 2 3 5 1 6 
 
2 3 4 1 5 6
 
2 3 1 4 5 6
 
2 1 3 4 5 6
 
1 2 3 4 5 6

以上是 $1 \sim 6$ 的排列，仔细观察会发现：冒泡排序的实质其实是从第一个数开始将该数移到第一个比它大的数的前面，并将两者之间的数前移一位。

接着分析,从 $5 4 2 3 6 1$ 到 $4 2 3 5 1 6$ 。被找出的数为 $5,6$ ,减少的逆序对为 $(5,4)$ ， $(5,3)$ ， $(5,2)$ ， $(6,1)$ 。

可以发现被找出的数前面都没有比它大的数。

原因：冒泡排序的一个特点为先将大的数换到末位。如果前面有比它大的数，那么一定是比它大的数优先往后换。

对于逆序对的减少，可以从两个角度入手：

视角 $1$ :对于减少逆序对中较大的数（也就是被找出的数），减少的逆序对的个数是与第一个比它大的数之间的数的逆序对。

视角 $2$ ：而对于减少逆序对中较小的数来说（也就是两者之间的数），减少的是与被找到的数之间的一个逆序对。

发现视角 $2$ 似乎比较好分析，一轮一个，那交换了几轮不就减少了几个吗。

于是我们统计逆序对(记数组名为 $cnt$ )时，可以从较小的数的视角统计，也就是对于一个数，统计在它前面比它大的数。

显然被找出来的数，逆序对的个数都为 $0$ 。那么逆序对个数不为 $0$ 的，就不是被找出来的数，那就是两者之间的数。由于每一轮两者之间的数都会 $-1$ 。总结一下就是所有逆序对不为零的数对减少逆序对的贡献就是 $\min(cnt_i,k)$ 。

计算时可以分类讨论，借助树状数组优化即可。

【code】

点击查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
#define ll long long
using namespace std;
ll n,m,a[200005],num[200005];
ll c[200005],t[200005],cnt[200005];
void add(ll *k,ll x,ll y){
	if(x==0) return;
	for(;x<=n;x+=(x&-x)) k[x]+=y;
}
ll sum(ll *k,ll x){
	ll ans=0;
	for(;x;x-=(x&-x)) ans+=k[x];
	return ans;
}
int main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
	ll ans=0;
	for(int i=1;i<=n;i++){
		ll k=sum(c,n)-sum(c,a[i]);
		ans+=k;
		add(c,a[i],1);
		add(t,k,k);
		add(cnt,k,1);
		num[a[i]]=k;
	}
	for(int i=1;i<=m;i++){
		ll op,x;
		scanf("%lld%lld",&op,&x);
		if(op==1){
			if(a[x]<a[x+1]){
				ans++;
				add(t,num[a[x]],-num[a[x]]);
				add(cnt,num[a[x]],-1);
				num[a[x]]++;
				add(t,num[a[x]],num[a[x]]);
				add(cnt,num[a[x]],1);	
			}
			else{
				ans--;
				add(t,num[a[x+1]],-num[a[x+1]]);
				add(cnt,num[a[x+1]],-1);
				num[a[x+1]]--;
				add(t,num[a[x+1]],num[a[x+1]]);
				add(cnt,num[a[x+1]],1);	
			}
			swap(a[x],a[x+1]);
		} 
		else{
			if(x>=n) cout<<"0"<<endl;
			else cout<<ans-(sum(t,x)+x*(sum(cnt,n)-sum(cnt,x)))<<endl;
		}
	}
	return 0;
}

区间增加，单点查询

【模板】树状数组2

思路剖析

相信经过上面的头脑风暴，再来看这题已经相当简单了。

此时主要运用到差分的思想,差分是前缀和的逆运算。

当要在区间 $[x,y]$ 加上 $k$ 时，我们进行以下操作：

$add(x,k) , add(y+1,-k)$

此时对于区间求前缀和对于 $x \sim y$ ，它的前缀和都为 $k$ ，而到 $y+1$ ,又变成 $0$ 。此时的前缀和正好是区间增加的数，且不会对其它数产生影响。

因此，当查询第 $x$ 个数时，只需要输出：

$a_x(第 x 个数原本的数值) + sum（x）(变化的值)$ 。

即可。

code

点击查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int a[500005],c[500005],n,m;
void add(int x,int k){
	for(;x<=n;x+=x&-x) c[x]+=k;
	return;
}
int q(int x){
	int sum=0;
	for(;x;x-=x&-x) sum+=c[x];
	return sum;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<=m;i++){
		int type;
		scanf("%d",&type);
		if(type==1){
			int x,y,k;
			scanf("%d%d%d",&x,&y,&k);
			add(x,k);
			add(y+1,-k);
		}
		else{
			int x;
			scanf("%d",&x);
			cout<<a[x]+q(x)<<endl;
		}
	}
	return 0;
}

posted @ 2023-01-19 17:26 k_stefani 阅读(79) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· DP做题合集

· P1972 [SDOI2009] HH的项链

· 树状数组专题

· 【寻迹#7】树状数组

· 理解树状数组这一篇文章就够啦

阅读排行：
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 单线程的Redis速度为什么快？
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决：字节Trae VS Cursor，谁才是开发者新宠？
· 展开说说关于C#中ORM框架的用法！

你好！晴天！

一蓑烟雨任平生。

树状数组笔记整理

树状数组介绍

树状数组功能

单点增加

动态维护前缀和

例题【具体应用】

【例题1】三元上升子序列

【例题2】 [USACO04OPEN] MooFest G 加强版

【例题3】P1972 [SDOI2009] HH的项链

例题3 update P2184 贪婪大陆

求逆序对

【例题】

【例题1】P2448 无尽的生命

【例题2】P3531 [POI2012]LIT-Letters

【例题3】P6186 [NOI Online #1 提高组] 冒泡排序

区间增加，单点查询

思路剖析

code

公告

搜索

常用链接

最新随笔

随笔分类 (23)

随笔档案 (16)

	void add(int x,int y){
	for (; x <= N;x += x&-x) c[x] += y;
	return ;
	}

	int ask(int x){
	int ans = 0;
	for (; x ; x -= x & -x) ans += c[x];
	return ans;
	}

	#include<iostream>
	#include<cstdio>
	#include<cmath>
	#define ll long long
	using namespace std;
	ll tree[100005],n,num;
	ll r[40005][2],a[100005];
	void add(ll x,ll y){
	for(;x<=100005;x+=(x&-x)) tree[x]+=y;
	}
	ll sum(ll x){
	ll ans=0;
	for(;x;x-=(x&-x)) ans+=tree[x];
	return ans;
	}
	int main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
	ll x;
	scanf("%lld",&x);
	a[i]=x;
	num=max(num,x);
	add(x,1);
	r[i][0]=sum(x-1);
	r[i][1]=sum(num)-sum(x);
	}
	ll ans=0;
	for(int i=1;i<=n;i++)
	ans+=r[i][0]*(sum(num)-sum(a[i])-r[i][1]);
	cout<<ans<<endl;
	return 0;
	}

	for ( int i = n; i; i --) {
	ans += ask (a[i] - 1);
	add (a[i] , 1 );
	}

	5 4 2 3 6 1

	4 2 3 5 1 6

	2 3 4 1 5 6

	2 3 1 4 5 6

	2 1 3 4 5 6

	1 2 3 4 5 6

你好！晴天！

一蓑烟雨任平生。

树状数组笔记整理

树状数组介绍

树状数组功能

单点增加

动态维护前缀和

例题【具体应用】

【例题1】 三元上升子序列

【例题2】 [USACO04OPEN] MooFest G 加强版

【例题3】P1972 [SDOI2009] HH的项链

例题3 update P2184 贪婪大陆

求逆序对

【例题】

【例题1】P2448 无尽的生命

【例题2】P3531 [POI2012]LIT-Letters

【例题3】P6186 [NOI Online #1 提高组] 冒泡排序

区间增加，单点查询

思路剖析

code

公告

搜索

常用链接

最新随笔

随笔分类 (23)

随笔档案 (16)

【例题1】三元上升子序列