P7114 [NOIP2020] 字符串匹配

题意

著名题目
链接

题解

参考博客
首先一个思路是 枚举循环节长度
要变成 \((AB)^kC\) 的形式 先枚举循环节\(AC\)长度\(i\)
设循环结长度为 \(i\) 显然 \(i\) 从 \(2\) 到 \(n-1\) 都是合法的
因为循环节非空且C非空
接下来我们想，能循环多少次呢？
这里引入扩展kmp函数\(Z[i]\) 表示从整个字符串从\(i\)号字符开始的后缀 和 整个串的 最长公共前缀
不妨自己画个图 \(t = Z[i+1]/i+1\) 就是最多能循环的次数（额外加上上循环一次）

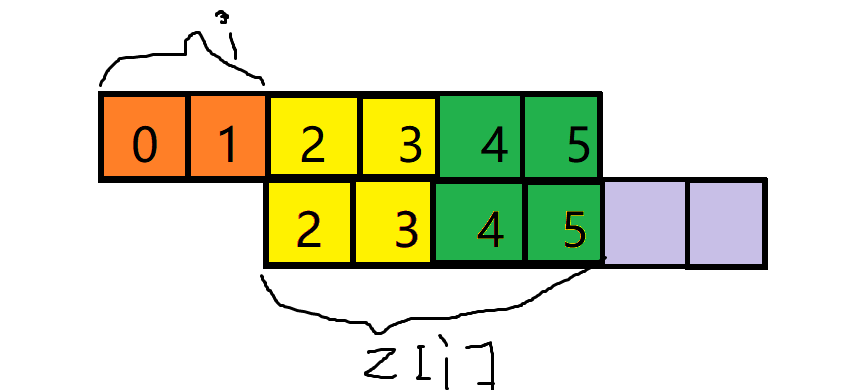
然后循环这么多次 到底有多少种合法的方案呢？
在这里 我们设\(pre sub all\) 表示前缀、后缀、整个串里面出现奇数次的字符的个数
在枚举i的过程中 我们可以很轻松的更新这三个值

对于循环节\(AB\) 我们分类讨论他出现了奇数次还是偶数次
如果出现了偶数次 那么对整个序列的影响可以忽视
也就是说 C中出现奇数次字符的个数 等于 整个序列出现奇数次字符的个数
也就是说 我们的序列A 需要奇数字符个数 小于等于 整个数列的奇数字符个数
对于这个数量的要求 可以用树状数组 维护\(F(x)\)表示\(0-i\)的所有前缀出现奇数次字符大于x的前缀个数
对于这个函数的求法 我们一会再做讨论
现在得出的结论是 这一部分对答案的贡献为

\[F(all)*(t/2) \]

接下来 如果出现了奇数次
思考后得出这一部分的贡献

\[F(suf)*(t-t/2) \]

最后 我们想想F(x)如何动态维护
每增加一个字符\(s[i]\)
我们把树状数组pre的位置+1
查询的时候可以求出在i之前的且出现奇数次字符小于等于某个数x的方案数
于是这题愉快的解决了

#include<bits/stdc++.h>
#define ll long long
#define inf 0x7fffffff
using namespace std;
#define maxn 1048576
int z[maxn];
char s[maxn];
int n;
int suf=0,all=0,pre=0;
int after[60],before[60]; 
void Z()//exkmp 
{
	z[0]=n;
	int now=0;
	while(now+1<n&&s[now]==s[now+1])now++;
	z[1]=now;
	int p0=1;
	for(int i=2;i<n;i++)
	{
		if(i+z[i-p0]<p0+z[p0])//够用 
		{
			z[i]=z[i-p0];
		}else
		{
			now=p0+z[p0]-i;
			now=max(now,0);
			while(now<n&&now+i<n&&s[now]==s[now+i])now++;
			z[i]=now;
			p0=i;
		}
	}
}
int c[maxn];
#define lowbit(x) (x&-x)
void Add(int x)
{
	while(x<maxn)
	{
		c[x]++;
		x+=lowbit(x);
	}
}
int Query(int x)
{
	int res=0;
	while(x)
	{
		res+=c[x];
		x-=lowbit(x);
	}
	return res;
}
signed main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		memset(z,0,sizeof(z));
		memset(c,0,sizeof(c));
		for(int i=0;i<=59;i++)after[i]=0,before[i]=0;
		scanf("%s",s);
		n=strlen(s);
		Z();
		all=pre=suf=0;
		for(int i=0;i<n;i++)
		{
			after[s[i]-'a']++;
			if(i+z[i]==n)z[i]--;
		}
		for(int i=0;i<26;i++)
		{
			if(after[i]&1)all++;
		}
		ll ans=0;
		suf=all;
		for(int i=0;i<n;i++)//枚举循环节长度i 
		{
			if(after[s[i]-'a']&1)suf--;
			else suf++; 
			after[s[i]-'a']--;
			if(before[s[i]-'a']&1)pre--;
			else pre++;
			before[s[i]-'a']++;
			if(i!=0&&i!=n-1)
			{
				int t=z[i+1]/(i+1)+1;
				ans+=1ll*Query(all+1)*(t/2)+1ll*Query(suf+1)*(t-t/2);
				//奇数偶数的答案要分开计算 
				//对于奇数次数 前面的奇数要比suf多 
				//对于偶数次数 前面的奇数要比总数多 
			}
			Add(pre+1);
		}
		printf("%lld\n",ans);
	}
	
	
	return 0;
}
/*
f[i][j]表示i到j出现奇数次的字符数量 
维护suf 表示后缀奇数次字符数量
    pre 表示前缀奇数次字符数量 
    all 表示总的奇数次字符数量 
树状数组 用来查询前缀中奇数次字符小于等于一个数p的有多少种 
Z[i]表示从i开始的后缀和整个数组的最大公共前缀 

*/