二元函数的极值与最值问题

目录

• 写在最前
• 二元函数极值点
• 二元函数最值

写在最前

对于形如\(z=f(x,y)\)的函数，求解极值的通法一般有两种：

• 偏导数法
• 二元全微分法

由于偏导数法操作简单，下面仅介绍这种方法

二元函数极值点

\(Ops:\)只想知道最值的可以跳过这一节。

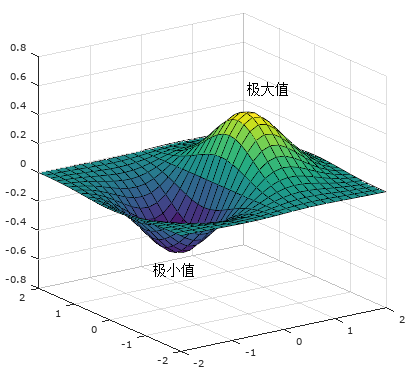
我们以驻点为圆心在\(xy\)平面上做一个圆（就如同在一元函数\(y=f(x)\)驻点附近找一段区间），若当半径足够小时，\(f(x_0,y_0)\)是该圆形区域的最大值或最小值， 那么该驻点就是极大值点或极小值点。与一元函数类似，驻点不一点是极值点。
那么我们如何判断极点呢？
一个比较常规的想法是，让\(f_x\)在\(x=x_0\)的两边异号，让\(f_y\)在\(y=y_0\)的两边异号，借此来判断函数的极值点。但有一个很明显的错误：

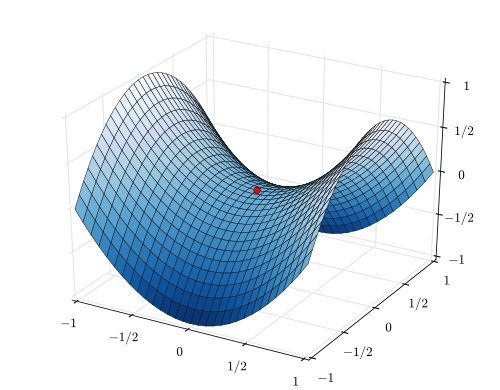
类比地理中的鞍部，这个点被称作鞍点。

那么，该怎么做呢，数学家想到了一种方法——二阶偏导法。
令

\[A=f_{xx}(x_0,y_0),B=f_{xy}(x_0,y_0),C=f_{yy}(x_0,y_0) \]

则有

\[A\times C-B^2>0 \text{$\large 且$} A>0==>\text{$\large 极小值$} \]

\[A\times C-B^2>0 \text{$\large 且$} A<0==>\text{$\large 极大值$} \]

\[A\times C-B^2<0==>\text{$\large 鞍点$} \]

\[A\times C-B^2==0 ==>\text{$\large 无法确定$} \]

二元函数最值

最值问题和极值问题相比，最大的区别就是最值问题可以通过比较各点的值来计算。我们可以通过求出所有极值点甚至非极值点的值来得出最终的答案。既然如此，我们可以求出所有可能的点（各偏导等于零的点）并计算得到最终答案。