科学计算与可视化

 

 

一.numpy库和matplotlib库的学习

　　（1）numpy库介绍：科学计算包，支持N维数组运算、处理大型矩阵、成熟的广播函数库、矢量运算、线性代数、傅里叶变换、随机数生成，并可与C++/Fortran语言无缝结合

　　　　　　np.array([1,2,3])列表转换为数组；np.array((1,2,3))元组转换为数组; np.array(range(5))把range对象转换为数组；np.arange(8)类似于内置的range()函数

　　　　　　np.linspace(0,10,11,endpoint = False)等差数组不包含终点

 

　　（2）matplotlib库介绍：是Python编程语言及其数值数学扩展包 NumPy的可视化操作界面。它为利用通用的图形用户界面工具包，如Tkinter, wxPython, Qt或GTK+向应用程序嵌入式绘图提供了应用程序接口（API）。此外，matplotli# -*- coding: utf-8 -*-

# -*- coding: utf-8 -*-
"""
Spyder Editor

This is a temporary script file.
"""
print("开始")

import numpy as np
import matplotlib.pyplot as plt
import matplotlib

matplotlib.rcParams['font.family']='SimHei' #设置默认字体
matplotlib.rcParams['font.sans-serif']=['SimHei'] #设置默认字体
labels = np.array(['第一周','第二周','第三周','第四周','第五周','第六周','第七周']) #
nAttr = 7 #边数
data = np.array([95,85,90,95,80,85,100]) #数据值
angles = np.linspace(0,2*np.pi,nAttr,endpoint=False) #角度设置，0-2PI，分隔7次
data = np.concatenate((data,[data[0]]))  #将数据和角度的数组首尾闭合，便于用plot函数绘制
angles = np.concatenate((angles,[angles[0]]))
fig = plt.figure(facecolor="pink")   #图形外的周边颜色
plt.subplot(111,polar=True)    #建立极坐标系的子分区
plt.plot(angles,data,'bo-',color='g',linewidth=2) #按照角度和数据画出不规则多边形
plt.fill(angles,data,facecolor='g',alpha=0.25)  #填充颜色
plt.thetagrids(angles*180/np.pi,labels)  #设置标签例如第X周
plt.figtext(0.52,0.95,'14-Kind的成绩图',ha='center') #设置标题
plt.grid(True)
plt.savefig('dota_radar.JPG')
plt.show()

 

效果图片：

 

三.自定义手绘风

代码如下：

# -*- coding:utf-8 -*-
import numpy as np
from PIL import Image

class picture:
    
    def __init__ (self,position):
        self.position = position

    def Hand_drawn_style(self):
        vec_el = np.pi/2   # 光源的俯视角度，弧度值
        vec_az = np.pi/3    # 光源的方位角度，弧度值
        depth = 6          # 深度权值，值越小背景区域越接近白色，值越大背景区域越接近黑色
        im = Image.open(self.position).convert('L')     # 打开图像并转变为灰度模式
        a = np.asarray(im).astype('float')
        grad = np.gradient(a)              # 取图像灰度的梯度值
        grad_x, grad_y = grad              # 分别取图像的横纵梯度值
        grad_x = grad_x * depth / 100.
        grad_y = grad_y * depth / 100.
        dx = np.cos(vec_el) * np.cos(vec_az) # 光源对x轴的影响
        dy = np.cos(vec_el) * np.sin(vec_az) # 光源对y轴的影响
        dz = np.sin(vec_el)                  # 光源对z轴的影响
        A = np.sqrt(grad_x**2 + grad_y**2 + 1.)
        uni_x = grad_x/A
        uni_y = grad_y/A
        uni_z = 1./A
        a2 = 255*(dx * uni_x + dy * uni_y + dz * uni_z) # 光源归一化
        a2 = a2.clip(0, 255)                 # 预防溢出
        im2 = Image.fromarray(a2.astype('uint8'))       # 重构图像
        im2.save('4d0424dd81_.jpg') # 保存图像
        im2.show()                # 显示图像

if __name__ =='__main__':
    position = '4d0424dd81.jpg'
    picture(position).Hand_drawn_style()

 

 

效果图：

 

 

 

四.正态分布图

代码

import numpy as np
import matplotlib
import scipy.stats
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab

if __name__ == "__main__":
    # 期望0，标准差1，条数50
    mu, sigma, num_bins = 0, 1, 500
    # 1M个随机数
    x = mu + sigma * np.random.randn(10000)

    # 正态分布的数据, 颜色的透明度0.5
    n, bins, patches = plt.hist(x, num_bins, density=True, facecolor='blue', alpha=0.5)
# 直方图函数，x为x轴的值，normed=1表示为概率密度，
#即和为一，绿色方块，色深参数0.5.返回n个概率，直方块左边线的x值，及各个方块对象
    # 拟合曲线
    y = scipy.stats.norm.pdf(bins, mu, sigma)
    plt.plot(bins, y, 'r--')
    plt.xlabel('Expectation')
    plt.ylabel('Probability')
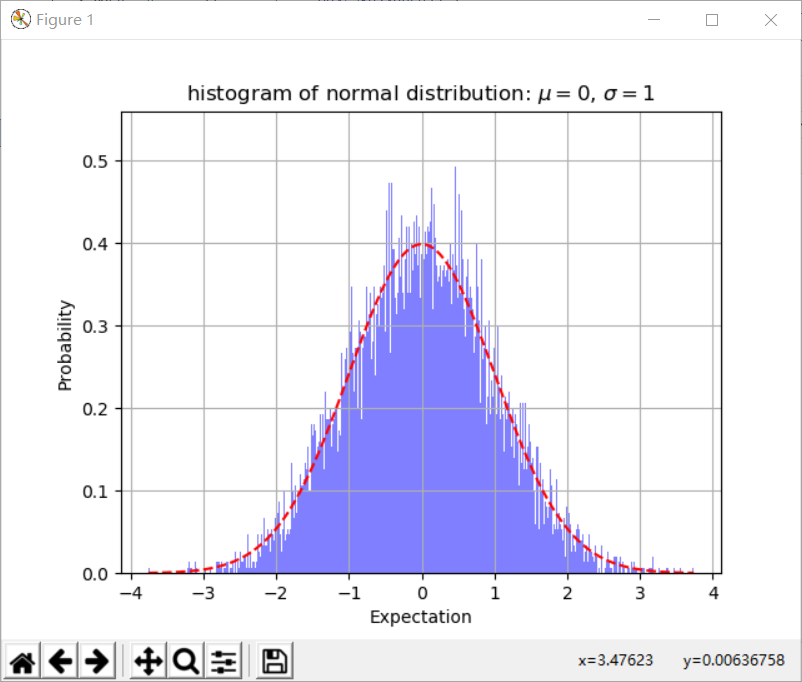
    plt.title('histogram of normal distribution: $\mu = 0$, $\sigma=1$')

    plt.subplots_adjust(left=0.15) #左边距
    plt.grid(True)  #打开网格线
    plt.show()

 

 

效果图片