DS博客作业05--查找
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
| 姓名 | 雷正伟 |
0.PTA得分截图
1.本周学习总结
1.1 查找的性能指标
- ASL成功
- 平均需要和给定值k进行比较的关键字次数称为平均查找长度（ASL）
- n是查找表中元素个数，
- Pi是查找第i个元素的概率（通常假设每个元素的查找概率相等，此时Pi=1/n）
- Ci是找到第i个元素所需要的关键字比较次数
- 一个查找算法的ASL越大，其时间性能越差，反之，若越小其时间性能越好
- ASL不成功
- 没有找到查找表中的元素，平均需要关键字比较次数
- 比较次数
- 对于一组数据当它以哈希表，链表，二叉搜索树储存时，关键字的搜索就要通过将关键字与其中的元素进行比较才能找到
- 哈希表因会有冲突导致关键字存储位置不是哈希函数所对应的位置，此时的比较次数就会增加
- 链表因会有冲突，导致关键字不是某一条链表的第一个元素，此时
1.2 静态查找
- 顺序查找：
在顺序查找表中，查找方式为从头扫到尾，找到待查找元素即查找成功，若到尾部没有找到，说明查找失败。所以说，Ci（第i个元素的比较次数）在于这个元素在查找表中的位置，如第0号元素就需要比较一次，第一号元素比较2次......第n号元素要比较n+1次。所以Ci=i；即
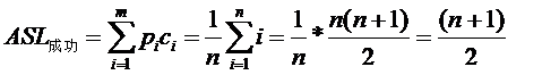
可以看出，顺序查找方法查找成功的平均 比较次数约为表长的一半。当待查找元素不在查找表中时，也就是扫描整个表都没有找到，即比较了n次，查找失败
代码
int SeqSearch(Seqlist R,int n,KeyType k)
{
int i=0;
while(i<n&&R[i].key!=k)i++;//从表头开始往下找
if(i>=n)return 0;//没找到则返回0
else return i+1;//找到则返回序号i+1
}
- 二分查找：
折半查找(二分查找)，首先待查找表是有序表，这是折半查找的要求。在折半查找中，用二叉树描述查找过程，查找区间中间位置作为根，左子表为左子树，右子表为右子树，，因为这颗树也被成为判定树或比较树。查找方式为(找k)，先与树根结点进行比较，若k小于根，则转向左子树继续比较，若k大于根，则转向右子树，递归进行上述过程，直到查找成功或查找失败。在n个元素的折半查找判定树中，由于关键字序列是用树构建的，所以查找路径实际为树中从根节点到被查结点的一条路径，因为比较次数刚好为该元素在树中的层数。所以
Pi为查找k的概率，level(Ki)为k对应内部结点的层次。而在这样的判定树中，会有n+!种查找失败的情况，因为将判定树构建为完全二叉树，又有n+1个外部结点(用Ei(0<=i<=n)表示)，查找失败，即为从根结点到某个外部结点也没有找到，比较次数为该内部结点的结点数个数之和，所以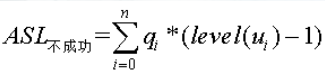
，qi表示查找属于Ei中关键字的概率，level(Ui)表示Ei对应外部结点的层次。所以，在一颗有n个结点判定树中，总数
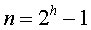，所以判定树高度为
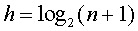的满二叉树,第i层上结点个数为
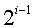，查找该层上的结点需要进行i次比较，因此，在等概率情况下ASL为
代码
int binarySearch(SeqList R,int n,KeyType k){
int low = 0, high = n-1, mid;
while(low <= high){
mid = (low + high) / 2;
if(R[mid.key] == k)return mid;//找到则返回下标
else if(R[mid].key > k)high = mid - 1;
elss low = mid + 1;
}
return 0;//找不到则返回0
}
1.3 二叉搜索树
1.3.1 如何构建二叉搜索树（操作）
- 第一步 给出一组元素
- 第二步 把第一个元素作为根节点
- 第二步，把第二个元素拿出来与第一个元素做比较，如果比根节点大就放在右边，如果比根节点小就放在左边
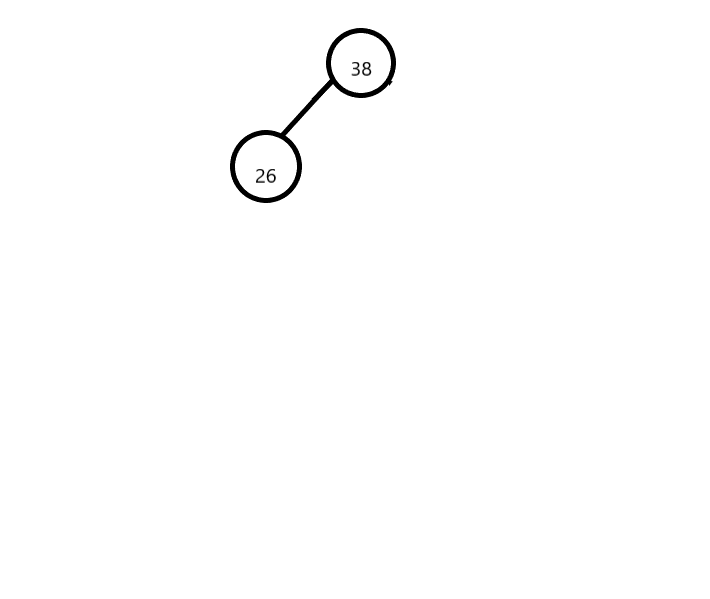
- 第四步 同样道理比较第三个元素62
- 第五步 插入第四个元素94，先与38比较，进入右子树，然后与62比较
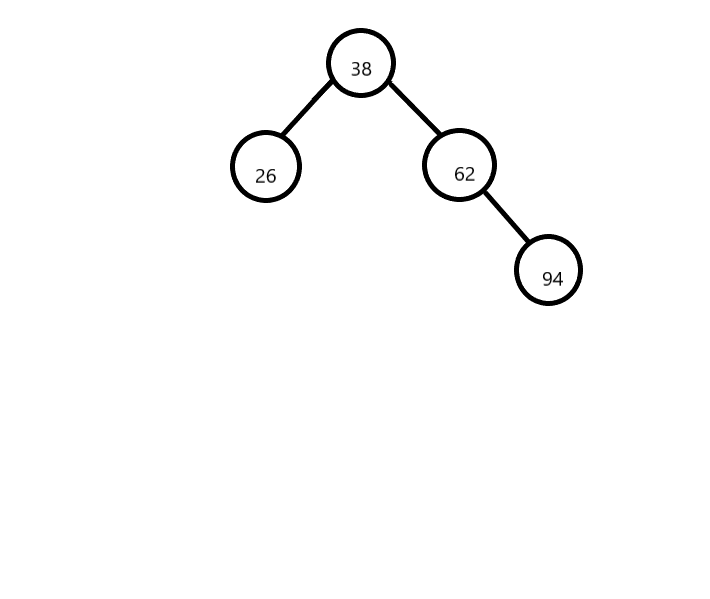
- 第六步 按照以上的方式依次把后面的元素插入到树中
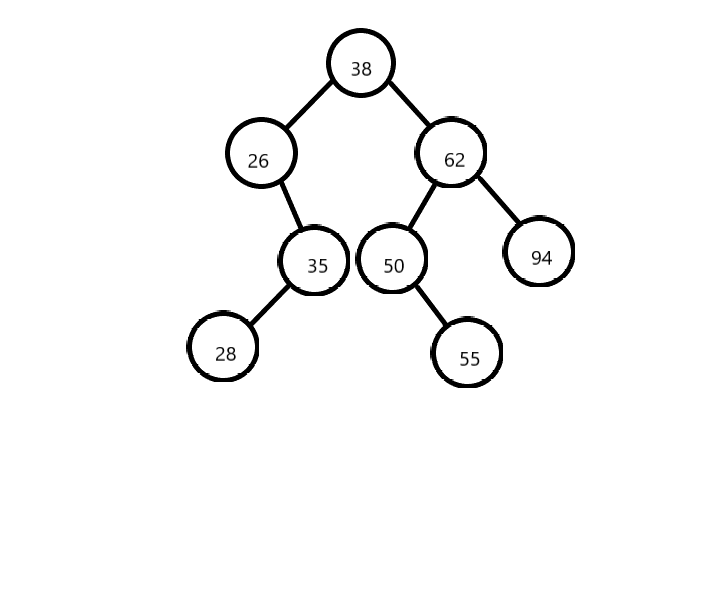
- ASL成功：将每层的节点数和层数相乘并求其的和再除以树的节点数
以上题为例：ASL成功=（11+22+33+42）/8=2.75 - ASL不成功：将每层的空节点数和层数-1相乘并求其的和再除以树的节点数
以上题为例：ASL不成功=（12+43）/5=2.8
1.3.2 如何构建二叉搜索树（代码）
- 二叉搜索树的构建
BSTNode* CreateBST(KeyType a[], int n)//创建二叉排序树
//返回BST树根结点指针
{
BSTNode* bt = NULL;//初始时bt为空树
int i = 0;
while (i < n)
{
InsertBST(bt, a[i]);//将关键字a[门插入二叉排序树bt中
i++;
}
return bt;//返回建立的二叉排序树的根指针
}
- 二叉搜索树的插入
bool InsertBST(BSTNode*& bt, KeyType k)
//在二叉排序树bt中插入一个关键字为k的结点,若插入成功返回真,否则返回假
{
if (bt == NULL)//原树为空,新插人的结点为根结点
{
bt = (BSTNode*)malloc(sizeof(BSTNode));
bt->key = k; bt->lchild - bt->rchild - NULL;
return true;
}
else if (k == bt->key)
return false;//树中存在相同关键字的结点,返回假
else if (k < bt->key)
return InsertBST(bt → > lchild, k);//插入到左子树中
else
return InsertBST(bt->rchild, k);//插入到右子树中
}
- 二叉搜索树的删除
bool DeleteBST(BSTNode& bt, KeyType k)//在bt中删除关键字为k的结点
{
if (bt == NULL)
return false//空树删除失败,返回假
else
{
if (k < bt->key)
return DeleteBST(bt->lchild, k);//递归在左子树中删除为k的结点
else if (k > bt->key)
return DeleteBST(bt->rchild, k);//递归在右子树中删除为k的结点
else//找到了要删除的结点bt
{
Delete(bt);//调用Delete(bt)函数删除结点bt
return true;//删除成功，返回真
}
}
}
void Delete(BSTNode*& p)//从二叉排序树中删除结点p
{
BSTNode* q;
if (p->rchild == NULL) //结点p没有右子树(含为叶子结点)的情况
{
q = p;
p = p->lchild;//用结点p的左孩子替代它
free(q);
}
else if (p->lchild = NULL) //结点口没有左子树的情况
{
q = р;
p = p->rchild;//用结点p的右孩子替代它
free(q);
}
else Delete(p, p->lchild);//结点p既有左子树又有右子树的情况
}
void Deletel(BSTNode* p, BSTNode*& r) //被删结点p有左、右子树,r指向其左孩子
{
BSTNode* q;
if (r->rchild != NULL)
Deletel(p, r->rchild);//递归找结点r的最右下结点
else//找到了最右下结点r(它没有右子树)
{
p->key = r->key;//将结点r的值存放到结点p中(结点值替代)
P->data = r->data;
q = r;//删除结点r
r = r->lchild;//即用结点r的左孩子替代它
free(q);//释放结点a的空间
}
}
- 时间复杂度：在O(log2n)到O(n)之间
- 减少代码量，同时便于删除和插入顺利找到父亲节点和孩子节点
1.4 AVL树
- AVL树：AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树(其特点是每个结点的平衡因子的绝对值小于或等于1)
- LL平衡旋转
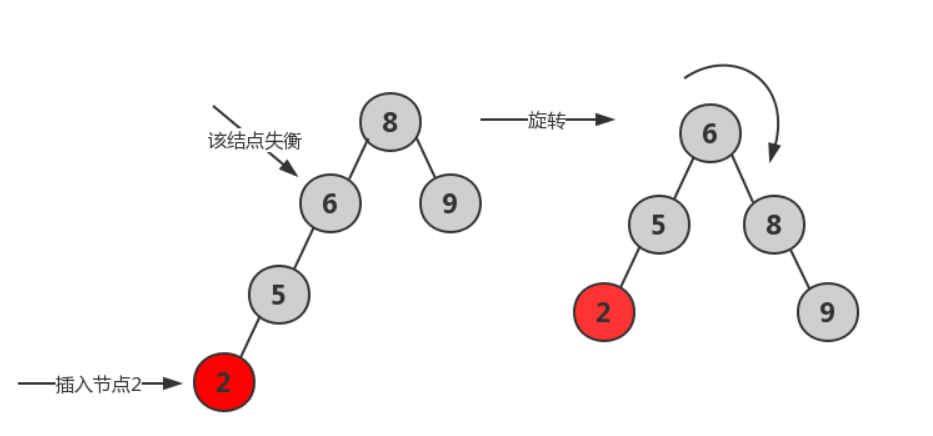
- RR平衡旋转
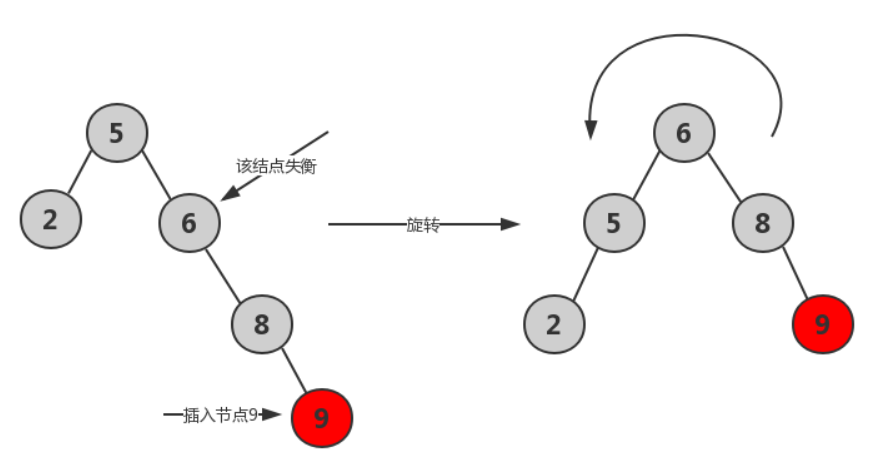
- LR平衡旋转*
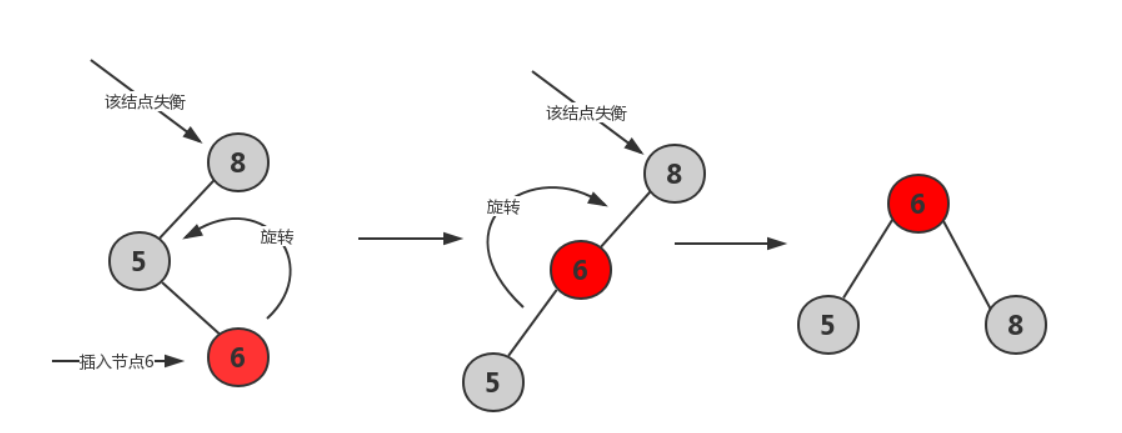
- RL平衡旋转*
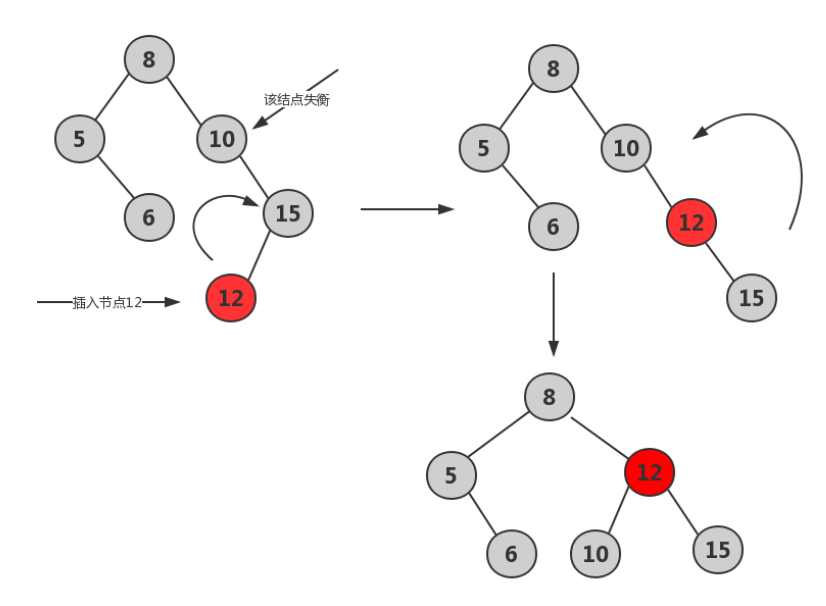
- AVL树的高度和树的总节点数n的关系：h≈log2N(h)+1
- Map是STL的一个关联容器，翻译为映射，数组也是一种映射。如：int a[10] 是int 到 int的映射，而a[5]=25,是把5映射到25。数组总是将int类型映射到其他类型。这带来一个问题，有时候希望把string映射成一个int ，数组就不方便了，这时就可以使用map。map可以将任何基本类型（包括STL容器）映射到任何基本类型（包括STL容器）。
| 用法 | 作用 |
| ---- | ---- | ---- |
| begin() | 返回指向map头部的迭代器 |
| end() | 返回指向map末尾的迭代器 |
| rbegin() | 返回一个指向map尾部的逆向迭代器 |
| rend() | 返回一个指向map头部的逆向迭代器 |
| lower_bound() | 返回键值>=给定元素的第一个位置 |
| upper_bound() | 返回键值>给定元素的第一个位置 |
| empty() | 如果map为空则返回true |
| max_size() | 返回可以容纳的最大元素个数 |
| size() | 返回map中元素的个数 |
| clear(） | 删除所有元素 |
| count() | 返回指定元素出现的次数 |
| equal_range() | 返回特殊条目的迭代器对 |
| erase() | 删除一个元素 |
| swap() | 交换两个map |
| find() | 查找一个元素 |
| get_allocator() | 返回map的配置器 |
| insert() | 插入元素 |
| key_comp() | 返回比较元素key的函数 |
| value_comp() | 返回比较元素value的函数 |
1.5 B-树和B+树
- B-树和AVL树区别
AVL树结点仅能存放一个关键字，树的敢赌较高，而B-树的一个结点可以存放多个关键字，降低了树的高度，可以解决大数据下的查找
B-树定义：一棵m阶B-树或者是一棵空树，或者满足一下要求的树就是B-树
- 每个结点之多m个孩子节点（至多有m-1个关键字）；
- 除根节点外，其他结点至少有⌈m/2⌉个孩子节点（至少有⌈m/2⌉-1个关键字）；
- 若根节点不是叶子结点，根节点至少两个孩子
- B-树定义
B树（英语：B-tree）是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。B树，概括来说是一个一般化的二叉查找树（binary search tree），可以拥有多于2个子节点。与自平衡二叉查找树不同，B树为系统大块数据的读写操作做了优化。B树减少定位记录时所经历的中间过程，从而加快存取速度。B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。
一颗m阶的B树定义如下：
- 每个结点最多有m-1个关键字。
- 根结点最少可以只有1个关键字。
- 非根结点至少有Math.ceil(m/2)-1个关键字。
- 每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
- 所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同。
- B-树的插入
- 如果该结点的关键字个数没有到达2个，那么直接插入即可；
- 如果该结点的关键字个数已经到达了2个，那么根据B树的性质显然无法满足，需要将其进行分裂
(分裂的规则是该结点分成两半，将中间的关键字进行提升，加入到父亲结点中，但是这又可能存在父亲结点也满员的情况，则不得不向上进行回溯，甚至是要对根结点进行分裂，那么整棵树都加了一层。)
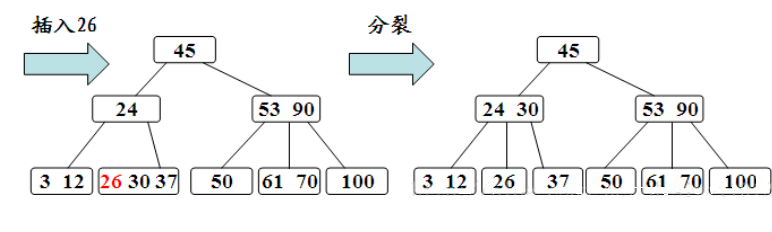
- B-树的删除
首先需要明确一点：删除非叶子结点必然会导致不满足B树性质，那么可以这样处理：被删关键字为该结点中第i个关键字key[i]，则可从指针son[i]所指的子树中找出最小关键字Y，代替key[i]的位置，然后在叶结点中删去Y。 因此，把在非叶结点删除关键字k的问题就变成了删除叶子结点中的关键字的问题了，那么B树的删除操作就变成了删除叶子结点中的关键字问题了。
如图，**被删关键字Ki所在结点的关键字数目等于ceil(m/2)-1，则需调整。 **
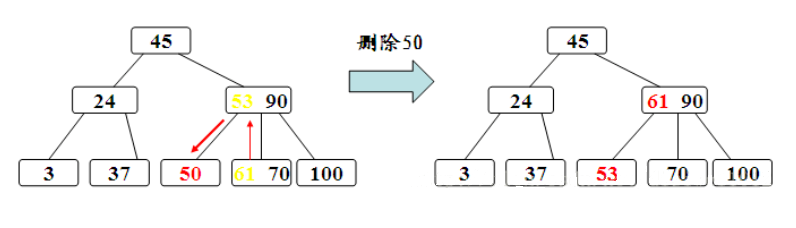
- B+树定义
B+树是一种树数据结构，通常用于数据库和操作系统的文件系统中。B+树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+树元素自底向上插入，这与二叉树恰好相反。
一个m阶的B树具有如下几个特征：
- 根结点至少有两个子女。
- 每个中间节点都至少包含ceil(m / 2)个孩子，最多有m个孩子。
- 每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m。
- 所有的叶子结点都位于同一层。
- 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
1.6 散列查找。
- 哈希表(Hash)
根据设定的哈希函数 H(key)和所选中的处理冲突的方法，将一组关键字映射到一个有限的、地址连续的地址集 (区间) 上，并以关键字在地址集中的“映像”作为相应记录在表中的存储位置，如此构造所得的查找表称之为“哈希表”。 - 解决哈希冲突
线性探测法
从发生冲突位置的下一个位置开始寻找空的散列地址。发生冲突时，线性探测下一个散列地址是：Hi=(H(key)+di)%m，（di=1,2,3...,m-1）。闭散列表长度为m。它实际是按照H(key)+1，H(key)+2,...,m-1,0,1,H(key)-1的顺序探测，一旦探测到空的散列地址，就将关键码记录存入
例如设一组初始记录关键字集合为(32，29，25，68，43，79)，散列表的长度为8，散列函数H(k)=k mod 7
其中不成功次数就是寻找到空位置时查找的次数
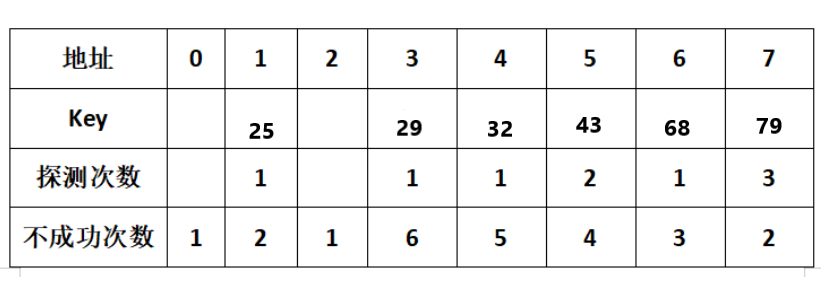
则，ASL成功=（14+21+3*1）/6=1.5；
ASL不成功=（1+2+1+6+5+4+3）/7=3.2
2.PTA题目介绍
介绍3题PTA题目
2.1 是否完全二叉搜索树（2分）
2.1.1 伪代码（贴代码，本题0分）
int main(）
{
输入结点数据；
层次遍历；
判断是否为完全二叉树；
}
BTree InsertTree(BTree T, int num)//建树
{
if 树为空
{
建新结点；
输入根结点数据；
左右子树分别初始化；
}
end if
else if (待插入数据大于根结点值)
在左子树插入该结点；
end if
else if (待插入数据小于根结点值)
在右子树插入该结点；
end if
返回建成后的树；
}
bool IsBST(BTree T)//判断是否完全二叉树
{
if 树空
return false;
引入队列Q；
将已建成的树的数据入队；
while 队列不空
{
if 左右孩子都存在
将左右孩子进队；
end if
else if 左孩子不存在，右孩子存在
return false;
end if
else 左孩子存在，右孩子不存在，或者左右孩子都不存在
{
if 左孩子存在，右孩子不存在
将左孩子进队；
end if
while 队列不空
{
指针指向队头；
出队；
if 左孩子不存在或右孩子不存在
return false;
end if
}
}
}
}
void LeverOrder(BTree T)//层次遍历
{
引入队列qu;定义指针p；
if 树为空
输出NULL;
end if
将该树数据入队；
while 队列不空
{
p指向队头；
输出p指向的值；
if 左孩子存在
右左孩子入队；
end if
if 左孩子存在
将右孩子入队；
end if
输出空格；//格式要求
}
}
2.1.2 提交列表
2.1.3 本题知识点
- 二叉搜索树的建立：由题面我们可以看到，题面要求我们左子树键值大，右子树键值小，故我们在建立二叉搜索树时，要注意如果待插入结点比当前结点小的话进右子树，比当前结点大进左子树；
- 完全二叉树：若一棵二叉树的高度为h，那么1到h-1层的结个数都达到最大，而最后一层结点连续且都集中在最左边。
- 完全二叉树的层次遍历特点：完全二叉树在进行层次遍历时，如果遍历到一个结点只有左孩子，或者左右孩子均为空时，那么剩余未遍历的结点，全都是叶子结点。
- 二叉树的层次遍历：和之前在树中学习一样，运用队列辅助实现；
- 二叉搜索树的插入操作：边查找边插入，算法中的根节点指针要用引用类型，这样才能将改变后的值传回给实参。
2.2 航空公司VIP客户查询（2分）
2.2.1 伪代码（贴代码，本题0分）
定义Hash类型变量H构建哈希链;
定义List类型变量ptr存储查找到的结点;
调用createHash函数构造哈希链H;
for (inti= 0;i <数据个数; i++) do
输入身份证信息和里程数;
if (里程数<最小里程数)
里程数=最小里程数;
end if
调用Insert函数向H插入结点;
end for
for (inti= 0;i <查找次数; i+ +) do
调用findKey函数在H中查找数据，将查找结果赋值给ptr;
if (ptr == NULL) do
查找失败;
else
查找成功;
end if
end for
2.2.2 提交列表
2.2.3 本题知识点
- 运用map容器
- 用了scanf和printf不会导致超时
2.3 基于词频的文件相似度（1分）
2.3.1 伪代码（贴代码，本题0分）
* 用map<string,bool>的数组来存放文件，每一个数据代表一个文件，每个文件内可以存多个词组，
string用来存单词，bool用来标记存在一个单词，方便后续单词数量的统计。
* same[101][101] 二维数组是相似矩阵，两个下标是所对应的文件的编号，
存的值是两个文件共有的单词数量。
* num[101]用来存放对应下标的文件所含有的词组的个数。
1.使用 cin.get()一个一个读取字符，直到遇到终止的字符'#'。
2.使用 toupper()函数将读入的小写字母转化为大写字母。
3.将输入的连续字母存入s_word数组（要求不超过10个）
4.中途遇到非字母字符或者超过10个的时候，都直接封尾，并存入map，
初始化s_word的下标继续读取数据。
数据的处理：
1.使用了C++中的迭代器，迭代统计每个map文件中的单词数量，并将每两个文件进行
一一的元素对比，如果数据相同的话，就在相似矩阵的对应位置的值加1.
2.对角线的元素本质上等于对应文件的单词数，可以对map求size()得到。
根据相似矩阵和长度表来计算相识度并输出：
用fixed函数和setprecision(1)来控制计算出来的数值的小数位数，并转化成文本形式。
2.3.2 提交列表
2.3.3 本题知识点
- 运用map容器下标可以自动排序的特点，对于计算相似度比较方便string s 字符串型变量
- 利用getchar()吸收回车
