1. 网上查询资料说明什么是fibnacci数列?
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·
斐波那契(Leonardo Fibonacci)以
兔子繁殖为例子而引入,故又称“兔子数列”,其数值为:1、1、2、3、5、8、13、21、34……在数学上,这一数列以如下递推的方法定义:
F(0)=1,
F(1)=1,
F(n)=
F(n - 1)+
F(n - 2)(
n ≥ 2,
n ∈ N*)。
1202年,斐波那契在《计算之书(
Liber Abaci)》中提出了斐波那契数列。根据该数列可折叠出
斐波那契蜗牛;绘制出
斐波那契螺旋线等。
[3] 此外,在现代物理、准晶体结构、化学等领域,该数列均有直接应用;为此,美国数学会从1963年起出版了一份名为《斐波那契数列季刊》的数学杂志,以专门刊载相关研究成果。 [1]
2. 给出fibnacci数列的递归表达式。
斐波那契数列的递归表达式可以表示为:
F(n) = F(n-1) + F(n-2),其中 n 大于等于 2,并且 F(0) = 0,F(1) = 1。
换句话说,斐波那契数列中的每一项都是前两项之和,起始两项为 0 和 1。
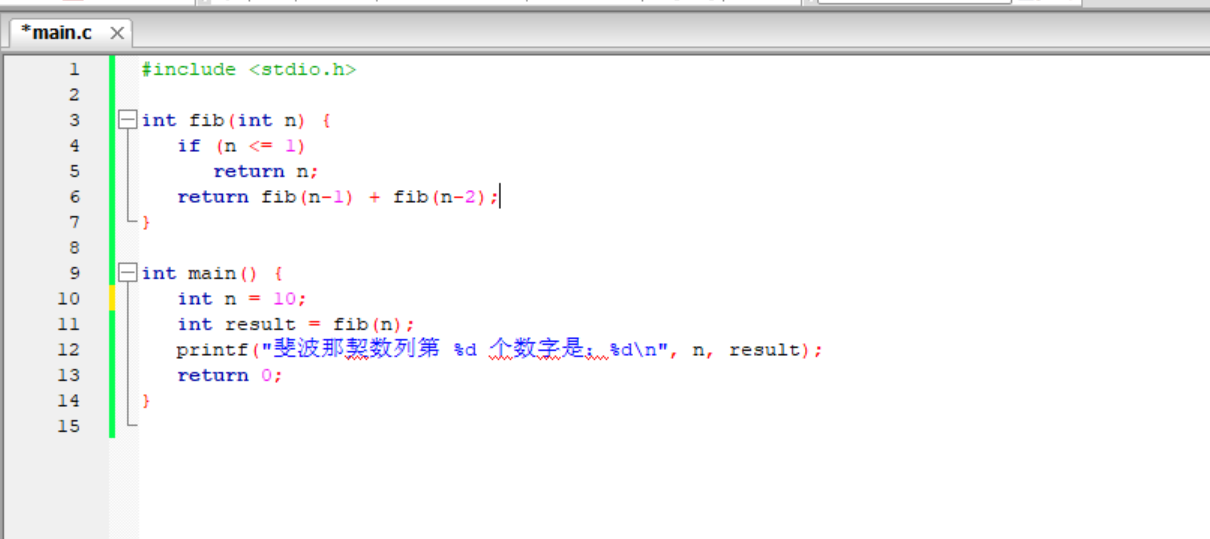
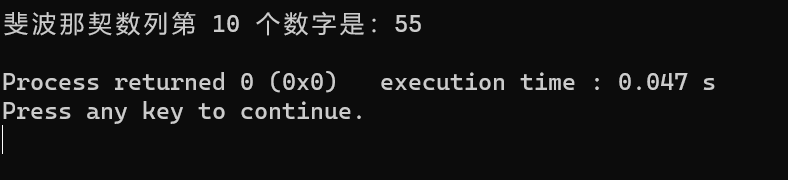
3. 用C语言递归实现Fib(n),并进行测试,提交代码和运行结果截图。在你的计算机上1分钟内能计算出fib(10),fib(100),fib(1000),fib(10000)吗?
可以
4. 加分项,用GDB查看递归的堆栈情况,提交截图。





